上市公司KMV模型适用性实证研究——以创业板高新技术企业为例

江苏大学 孔玉生 张文君

一、引言

美国次贷危机的爆发、扩散，欧债危机的爆发一次又一次向全球敲响了信用风险管理的警钟，信用风险的度量技术和管理方法成为理论界和实务界关注的焦点。违约率是信用风险中的最主要因子，从某种程度上讲，信用风险就是违约风险。高新技术企业处于创业期、成长期，业绩不稳定，规模较小，是风险企业的一种。高新技术企业的高风险性使其在生产经营活动中面临诸多不确定性因素，这些不确定因素经过积累会逐渐加深，导致企业业绩下滑，资金周转失灵，甚至面临破产清算的危机，进而导致高新技术企业违约的发生。因此，有效地评估违约概率是保证高新技术企业规模扩大，业绩增长的基础和关键，同时也为商业银行对高新技术企业进行信用风险评估提供有力的依据。

目前主流信用风险度量模型有四种，分别为以下四个高级信用风险模型：J.P. Morgan 的Credit Metrics 模型、CSFP 的Credit Risk+模型、KMV 公司的KMV 模型和麦肯锡公司的CPV 模型。由于高新技术企业的风险较高，股价波动较大，而KMV 模型则是以股价波动为主要指标来预测违约概率的，因此本文重点分析以期权理论为基础的违约概率预测模型：KMV 模型。

二、KMV 模型理论架构

（一）KMV 模型理论基础：默顿模型 莫顿模型（1974）是一个完全依赖于公司实际资本结构的模型。在该模型中，他假设公司有很简单的资本结构：其资产价值为V，其融资来源为股权S 和一种债务工具，债务工具的到期日为T，当前价值为D。根据假设，可以将该公司的资产负债关系表示如下V=D+S。假设没有交易费用，则债券到期日T 时，公司的股权价值为：

由于假设股票市值加上债券价值等于公司的总价值，所以公司债券的价值为:

根据上述股权价值的表达式，由图1 可见，公司股权价值的损益分布类似于一个看涨期权，OB 是经过折现后的企业负债数量，OA 和OC 分别代表在企业负债到期时可能存在的两个资产市值。如果负债到期时企业资产处在OA 水平，此时OA＜OB，企业出现资不抵债，此时公司具有违约动机，因为在这种情况下，公司宁愿将股票资产全部转给债权人，也不愿意再去筹措资金抵偿债务；如果负债到期时企业资产处在OC 水平，OC＞OB，此时企业不会违约，其股权价值为BC（OC 与OB 之差）。M 为股东对公司的初始投资。由于公司股东有限责任的特性，可以将公司股票视为资产价值的看涨期权，标的物为公司资产市场价值，执行价格是与公司资产结构有关的“违约边界”。

图1 股权价值与公司资产价值的关系

（二）默顿模型扩展：KMV 模型

（1）KMV 模型的求解原理。默顿模型之后出现了很多方向的演变，其中KMV 模型就是其一。KMV 模型主要是运用预期违约概率EDF 的值来评估公司在未来一段时期发生违约的可能，模型共分三个步骤来确定EDF。首先，从公司股权的市场价值、股价的波动性及负债的账面价值估计出公司资产市场价值及其波动性。然后，根据公司的负债计算出公司的违约点，还要根据公司的现有价值确定出公司的预期价值，用这两个价值以及公司价值的波动性求出违约距离DD。最后，根据违约距离DD 和历史违约概率之间的映射函数最终确定公司违约概率。由于我国历史违约数据的积累工作滞后，违约距离和实际违约频率之间的映射仍然无法实现，而通过公式直接计算出的理论违约率的结果偏差很大。因此，本文直接应用违约距离来比较上市公司的相对违约风险大小。

（2）KMV 模型求解原理的修正及计算步骤。具体如下：

第一，估计上市公司股票价格波动率σE。股票价格满足对数正态分布，假设在第i 天末市场的股票收盘价为Si，定义μi为在第i 天内(即第i-1 天末到第i 天末之间)的连续复利收益率，则有股票日收益率：μi=ln（Si/Si-1），则股票收益率日标准差为：

第二，计算公司资产价值σV和资产波动率σA。KMV 模型中的资产价值V 和资产波动率σA可以通过联立Black-Scholes 期权定价公式求出：

第三，计算违约距离DD。KMV 模型假设企业资不抵债时违约，违约距离被定义为要达到违约点，资产价值需下降的百分比对于资产价值波动的标准差的倍数，其表达式为:

其中，E（V）为债务到期时公司资产价值的期望值；σA为公司资产价值波动率；DPT 为违约点；T 为债务期限。

三、KMV 模型实证研究——以高新技术企业为例

（一）样本选取 本文从创业板中随机选取新制造业、信息技术、生物医药技术、新材料技术的7 家高新技术行业公司作为研究样本（表1）。为了验证KMV 模型的甄别能力，再随机选取与之总资产规模相近的7 家隐含风险的创业板上市公司（如净利润增长率连续两年为负、业绩大幅下滑、股价大幅下跌等）作为研究样本进行对比研究。样本的财务数据和市场数据来自国泰安CSMAR数据库和巨潮资讯网。本文最终选取的样本如表1 所示：

表1 样本来源

（二）参数设定 具体如下：

（1）股权的市场价值E 的计算。由于股权分置改革是在2005年开始进行的，主要是解决2005 年之前上市公司的非流通股问题。而创业板是在2005 年之后才成立的股票板块，所以在计算股权市场价值时不存在非流通股的问题。所以，本文选用2011 年一整年的每周个股总市值的平均值为依据来计算股权价值，每周个股总市值为每周收盘价与个股发行总股数的乘积，即股权市场价值为：（每周收盘价×周发行总股数），其中n 为周数。

（2）无风险利率。本文采用国内多数学者使用较多的中国人民银行公布的银行业一年期定期存款利率来代替无风险利率。但由于2011 年央行多次调整利率，为更加准确的确定这一数值，本文采用加权平均的方法计算无风险利率，具体算法见表2。

表2 无风险利率

（3）违约点的选取。实务中，通常采用选择短期债务（STD）面值与长期债务（LTD）面值的一半两者相加来计算违约触发点。但由于高新技术企业作为风险企业，其风险性极高，所以不能简单的利用原始KMV 模型中的系数。为了更灵敏的评估信用风险，本文将长期债务面值系数选取为0.5、0.75、0.35，来验证哪一系数可以更精确的评估高新技术企业的信用风险，即：

（4）公司资产价值预期增长率g 的确定。为了更好地反映高新技术企业的发展状况，本文采取以下方法计算公司资产价值预期增长率：

为了消除短期资产波动的影响，本文选取计算基点前三年平均值作为计算结果。对于那些缺少相应年份的资产负债表数据的公司而言，将使用两年平均值来代替。

（5）债务期限T 的确定。KMV 公司在应用模型时规定债务期限为一年，即信用风险每一年更新一次。所以，本文也将时间范围设置为一年，即T=1。

（三）实证结果 首先求出年平均股权价值E，然后根据每只股票的日收盘价，通过Excel 求出股权价值波动率σE。之后根据每只股票的流动负债和非流动负债面值求出DPT1、DPT2、DPT3，其计算结果见表3。KMV 模型共需7 个参数，其中4 个参数（股权价值，负债账面价值，无风险利率，负债期限）可以从市场信息中得出，股权价值波动率也通过每日收盘价求出。其余两个参数（隐含的资产市场价值、隐含资产价值波动率）则需要通过上述5 个参数联立KMV 方程组借助Matlab 软件迭代得出，计算出上市公司的资产市场价值和资产价值波动率，其计算结果见表4。待7 个参数都已确定，再根据前文所述的公司资产价值预期增长率的确定方法得出每只股票的资产预期增长率g，然后将KMV 模型的7 个参数和g 一并带入违约距离DD 的计算公式，其计算结果见表5。

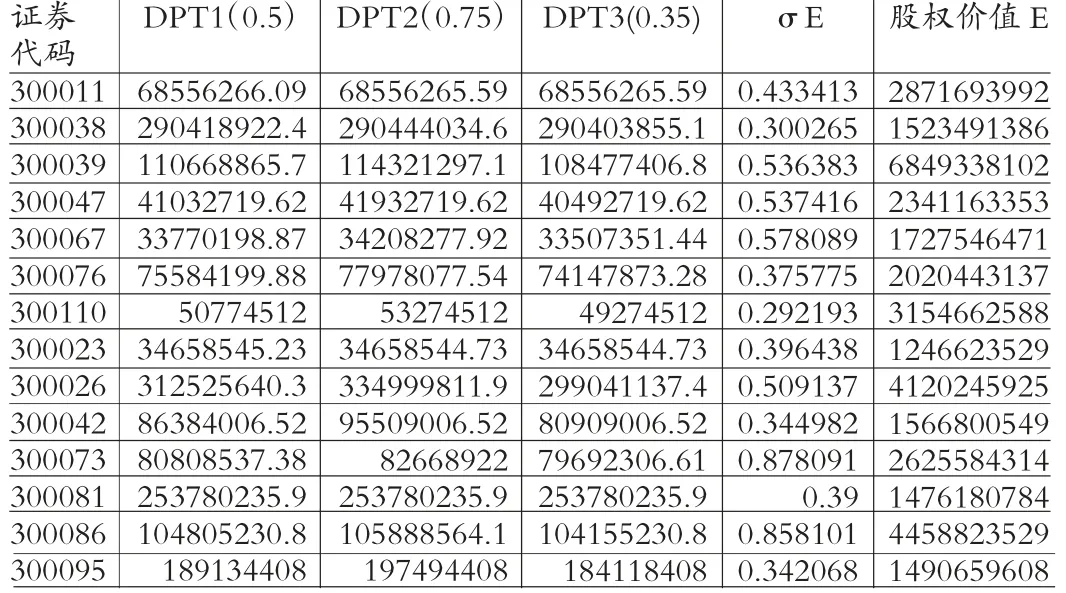
表3 违约点、股价波动率及股权价值

（四）实证结果的检验与分析 为了比较隐含风险公司和正常业绩公司违约距离DD 的差异是否显著，本文选用SPSS 软件对实证结果进行比较分析。通过SPSS 软件进行两配对样本T 检验，从表6 中可以看出，正常公司的违约距离明显大于风险公司，说明正常公司的信用风险较小。但是，由表7 中却发现，尾概率Sig.都远大于显著性水平α=0.05，所以配对变量均线性相关。再由表8 中看出，DD1、DD2、DD3的双侧尾概率Sig.（2-tailed）均大于显著性水平α=0.05，且三者都满足t∈置信区间I，则认为隐含风险公司和正常业绩公司的违约距离不存在显著性差异。这就说明无论是隐含风险公司还是正常业绩公司都存在较高的信用风险，它们之间的风险性不具有显著性差异，这也同高新技术企业风险性极高的特点相符合的。

表4 资产市场价值及波动率

表5 资产预期增长率及违约距离

表6 均值表

表7 相关性检验表

表8 T 检验表

再由表8 的T 检验表中DD1、DD2、DD3的t 值的大小和双侧尾概率Sig.（2-tailed）的大小排列可以表明，DD3对于两种风险公司的区分度最高，其次是DD2、DD1，这一结论从相关性检验表中也可以得出。这一结论为今后将KMV 模型用于高新技术企业信用风险评估研究中提供了设置违约点的依据。

四、结论及建议

（一）研究结论 本文通过随机选取两组风险性具有区分度的创业板股票进行实证分析，其结果表明，隐含风险的股票和正常业绩股票的违约距离只是在均值上有所差异，而通过科学的统计检验表明其二者不存在显著差异，因此，修正后的KMV 模型不能很好的区分两组创业板股信用风险的差异。但是，创业板高新技术企业本身就是风险性极高的一类行业，无论是隐含风险股票还是正常业绩股票都存在着较高的风险，该实证结论也正好验证了创业板股的这一特征，也就说明了KMV 模型能够较好的评估创业板股票的信用风险。再者，检验结果也表明，在使用KMV 模型对高新技术企业进行违约估计时，违约点的选取采用短期债务加上长期债务的0.35 能够更灵敏的区分违约风险。这也为今后KMV 模型的研究提供一个更加明确的参数设置依据。

（二）相关建议 目前，通过结构模型对高新技术行业进行违约预测的文献还不多，KMV 模型在高新技术行业中的适用性也不清晰，并且存在诸多问题，笔者根据本文研究，对今后KMV 模型在创业板高新技术企业的推广和应用提供几点建议：第一，加强我国创业板资本市场的建设。KMV 模型所使用的股价信息都是从股票市场获得，而我国创业板市场在制度方面还存在诸多缺陷，时有投机炒作等操纵股价的行为产生，股票价格波动很大。因此，国家应该逐渐完善创业板资本市场的建设。第二，加强创业板上市公司的会计审核与信息披露制度。会计数据是KMV 模型的重要输入变量，其准确程度对模型的有效使用有着重要意义。创业板上市公司在会计审核方面基础薄弱，这就容易导致会计信息失真等现象的滋长。因此，这就需要监管者加强公司财务信息真实性和可靠性的监督，同时企业也要提高自身的内部控制和信息披露制度。第三，逐步建立起我国自己的违约数据库。违约距离DD 和预期违约频率EDF 值的映射关系在我国尚未建立，由于宏观经济的差异，在我国不能直接使用国外已经建立的映射关系数据库。因此，目前KMV 模型在我国的实证研究停滞于违约距离DD 的确定阶段，无法准确确定EDF，而EDF 才是该模型的最终输出结果。

［1］金戈：《高新技术企业的性质》，《工业技术经济》2005 年第24 期。

［2］阿诺.德.瑟维吉尼,奥利维尔.雷劳特著.任若恩等译：《信用风险—度量与管理》中国财政经济出版社2005 年版。

［3］乔木青、刘强：《KMV 模型在中国的适用性研究》，西南财经大学2011 年硕士学位论文。

［4］王周伟：《风险管理》机械工业出版社2012 年版。

［5］吴恒煜：《信用风险控制理论研究》经济管理出版社2006年版。