基于响应面优化的结构有限元模型修正

鲍 诺 王春洁

(北京航空航天大学 机械工程及自动化学院，北京100191)

在航空航天等领域存在大量的复杂结构，由于分析过程中的众多不确定因素以及引入多种假设的建模等效简化，如材料、边界条件、结构连接等误差和局部或整体的非线性等，造成有限元计算值与试验值之间存在差异[1－2].因此，有必要利用试验数据对模型进行修正，以便提高有限元模型的计算精度.

模型修正作为动力学的逆问题，可转化为对设计参数的优化.张保强等以弹性模量、刚度等变量为修正参数对复杂边界弹性梁有限元模型进行迭代修正[3].王永华等为匹配真实模型应用熵判别粒子群法对发动机性能参数进行有限元模型迭代修正[4].Coppotelli等基于灵敏度分析的模型修正方法对织女星运载火箭的上部结构系统(UCMEC，Upper Composite Mechanical Configuration)进行迭代修正，修正后模态频率与试验值误差明显减小[5].Davoodi等利用遗传算法对典型球关节系统的参数进行有限元模型迭代修正，结果显示模型具有良好的预测精度[6].Mthembu等以梁单元弹性模量为变量结合粒子群法研究了H梁有限元模型迭代修正中最优模型的选择[7].可见模型参数修正总是需要面对参数筛选和有限元模型反复迭代的情况.

本文针对模型修正过程中模型迭代困难及模型参数选择且可能存在多工况的问题，提出响应面优化的方法进行模型修正.采用统计分析中F检验筛选修正参数来构造响应面，用响应面来替代有限元模型结合遗传算法进行优化，避免迭代过程每次调用有限元程序.以三自由度系统数值模型来验证待修正模型中参数多工况时，响应面优化的模型修正能力.以GARTEUR模型来检验参数筛选后响应面优化的修正结果，通过三级预示水平来验证修正后模型具有一定的普遍适用性，进而证实参数筛选后响应面优化的模型修正方法的有效性.

1 响应面优化的模型修正原理

1.1 4阶多项式响应面模型

响应面法将试验设计和数理统计相结合，通过样本点拟合出响应面函数来模拟输入(参数)－输出(响应)的隐式关系.常用的试验设计有中心复合设计、正交设计、全因子设计、拉丁方抽样等.由于样本点在修正参数区间的分布对响应面的近似精度影响较大，因此本文在拉丁方试验的基础上增加一个准则[8]，求得此准则下最优的拉丁方设计.其试验设计矩阵每列中各个水平出现的次序和各个样本点的因子水平分布更均匀，抽样效果好.

采用非线性拟合精确度更高的不完全4阶多项式作为响应面近似函数，将试验设计的多组采样点及响应值运用回归、拟合等方法构建响应面模型，其响应面近似函数形式为

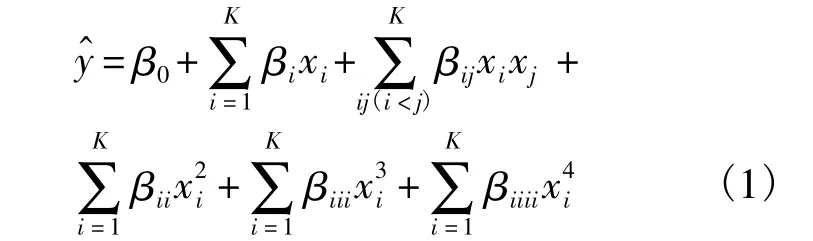
式中，xi为修正设计参数;K为修正设计参数的个数;β0，βi，βij，βii，βiii，βiiii为不完全 4 阶多项式待定系数.

由试验设计确定的样本点组成修正设计参数矩阵X，同时可得有限元模型计算值向量Y;假设有限元计算值与响应面拟合值误差组成的向量为ε，则各矩阵向量之间的关系如式(2)所示.根据最小二乘法，由式(4)和式(5)可得式(6)，求解出不完全4阶响应面函数的系数向量β[9].

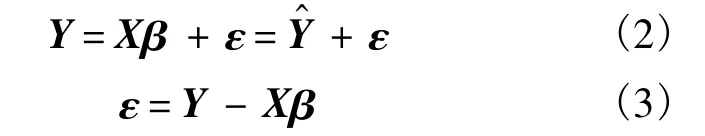
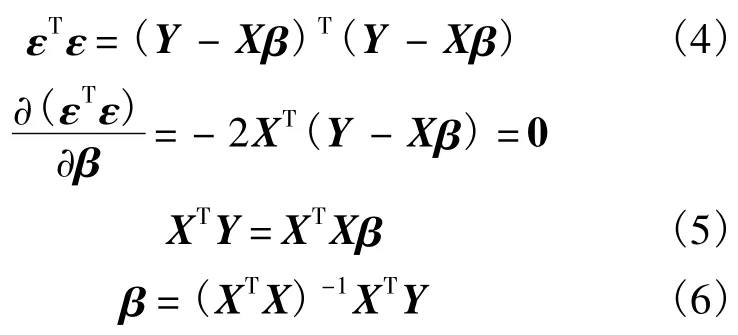
由待定系数β可得到响应面函数的表达式.

1.2 响应面有效性检验

判断拟合的响应面模型是否可信，通常用均方根误差(RMSE)相对值和决定系数(R2)两个标准对样本数据的拟合精度检验，分别如式(7)和(8)所示.RMSE→0表示响应面误差小;R2→1表示响应面与原模型相似程度高.

1.3 F值检验分析

由结构的特点初步选取待修正参数，然后分析参数对各阶频率影响的显著程度，筛选出对频率影响显著的参数，忽略影响小的参数.本文采用F值检验法对修正参数筛选.利用试验设计在参数的设计空间内确定样本点并进行有限元计算获得样本响应频率，然后对样本进行F值检验，分析多个因素(如刚度、密度、弹性模量等)对模态频率的影响是否显著.与传统的灵敏度参数筛选方法相比，F值检验法是从全局角度出发，在整个设计空间中筛选对特征量有显著影响的参数，避免了灵敏度分析只计算参数在某设计点处局部梯度的问题.

假设对有限元模型的修正参数A进行F检验，则 A 的 F 值为[10]

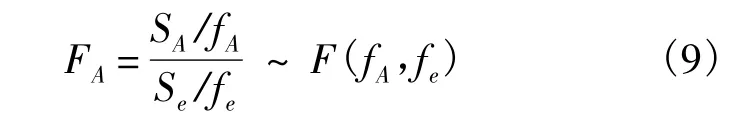
式中SA和Se分别为因素A和误差e的偏差平方和;fA和fe分别为因素A和误差e的自由度.给定显著水平 θ=0.05，使得

对于取定的样本值，由式(9)计算得到FA，则

1) 若 FA≥F1－θ(fA，fe)，即 P≤0.05，则变量对响应的影响显著;

2) 若 FA＜ F1－θ(fA，fe)，即 P ＞0.05，则变量对响应的影响不显著.

2 响应面优化的模型修正流程

2.1 目标函数

结构有限元模型修正通过将试验值和响应面值相结合，构造出优化目标函数，将模型修正转换为优化问题.

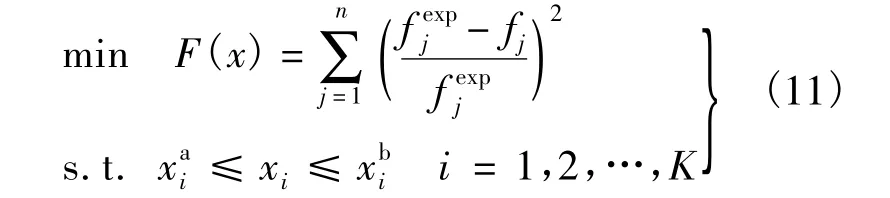
式中，F(x)为实测频率与响应面计算频率相对误差的平方和;为第j阶实测模态频率;fj为第j阶响应面计算频率;n为参与修正频率的阶数;xi为第i个修正参数，分别为修正参数上下限;K为修正参数的个数.

2.2 模型修正流程

由于模型的多个样本点计算，将初始有限元模型选定的修正变量参数化，建立参数化模型.实现响应面优化的模型修正流程模块化，见图1.主要修正流程为:首先初始模型进行参数化，其次筛选显著性修正参数构建响应面模型，再次对响应面参数进行优化，最后将参数优化结果代入初始有限元模型中，对修正结果进行验证.

图1 基于响应面优化的模型修正流程

3 三自由度系统数值算例

三自由度弹簧－质量系统[11]如图 2所示.mi=1.0 kg(i=1，2，3)，ki=1.0 N/m(i=3，4)，其中mi为i号质量块质量，ki为相应的弹簧刚度.模型修正中所有的误差参数已知，假设3个待修正参数变量的初始值为:k1=k2=k5=2.0 N/m，然而3个变量真实试验值为:k1=k2=k5=1.0N/m，与真实值相比，误差为100%.

图2 三自由度弹簧－质量系统

模型建模过程中，通常会有未考虑到的参数存在问题，例如真实系统中某个参数不存在或者存在误差，在此工况下进行模型修正，验证响应面优化的模型修正能力.假定工况1为标准工况，连接值k6=3.0 N/m(准确值)，除了初始设定的k1，k2，k53个待修正参数，不存在其他误差参数;工况2为模型中连接值k6不存在，即k6=0 N/m，其他与工况1相同;工况3为模型中存在连接误差，即k6=3.5 N/m，其他与工况1相同.

根据模型修正流程构建三自由度数值算例3种工况的响应面模型.3种工况的响应面模型检验结果，如图3a和图3b所示，其均方根误差相对值和决定系数分别趋向0和1，可以准确描述三自由度数值算例的结构参数与响应的关系.

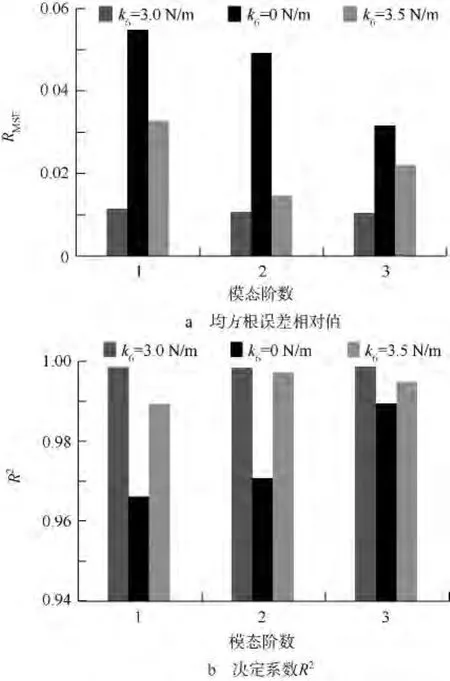
图3 三自由度模型3种工况响应面有效性评价

三自由度数值模型的3阶试验频率和响应面计算频率构造的目标函数，如式(11)所示.采用遗传算法优化，其迭代收敛曲线如图4所示.

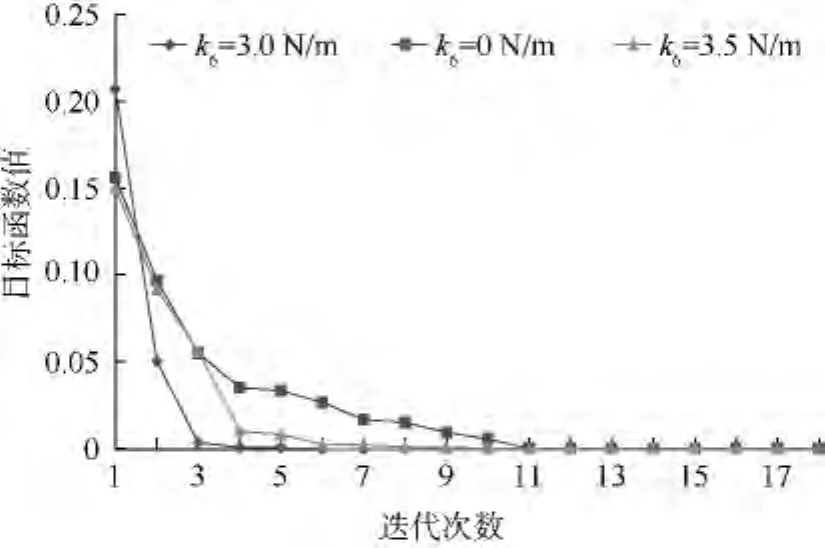
图4 三自由度模型3种工况目标函数收敛曲线

3种工况修正前后结果如表1所示，工况1输入参数k1，k2，k5(N/m)的误差由100%降低到2%之内，代入有限元模型得到的输出频率f1，f2，f3(Hz)的误差都在1%之内.

工况2和工况3由于待修正模型中k6=0 N/m(不存在)和k6=3.5 N/m(有误差)的原因，修正后输入参数k1，k2，k5必然出现较大偏差，但是模型修正后的输出3阶频率f1，f2，f3误差全部降低到2%之内.因此待修正模型中即便有参数被剔除或者存在误差，响应面优化法的模型修正也能获得准确的模态频率修正值，具有良好的模型修正能力.

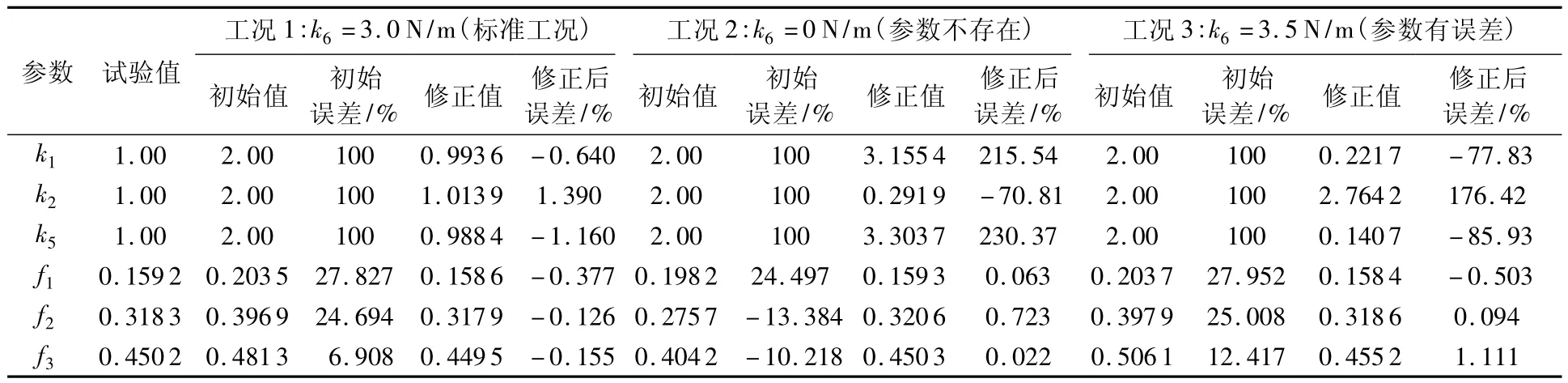
表1 三自由度模型修正前后参数值

4 GARTEUR模型修正与预测

4.1 初始模型构建

GARTEUR飞机模型由法国国家航空航天研究院设计制造，该模型具有低刚度、高柔度、模态频率低且密集的特点，可以用来评估动力学试验与模型修正技术[12－13].飞机模型由矩形截面的铝制梁构成，其中机身长1.5 m，翼展2.0 m，机翼上表面附着一层黏弹性阻尼材料.主要包括机身、机翼、水平尾翼、垂直尾翼、两边小翼等部件，如图5所示.

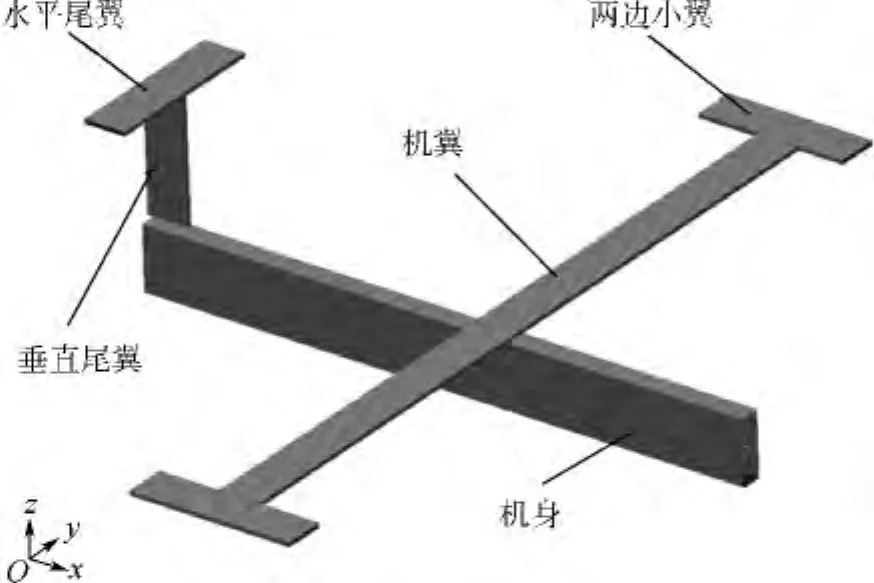
图5 GARTEUR结构模型

由于GARTEUR模型各部件细长的特点，主体结构采用梁单元模拟，其有限元模型如图6所示.机翼连接处为两个对称刚性单元，垂直尾翼与机身连接为刚性单元，机身与机翼连接为BUSH单元.在各部件的螺栓等连接处相应地增加集中质量单元来模拟连接件质量.初始模型中各部件的几何和材料参数相对准确，但结构连接处模型简化较多、误差较大，因此需要对模型进行修正.

图6 GARTEUR有限元模型

根据建模过程中连接结构的特点，初步选出x1～x12共12个待修正参数，分别为:机身/机翼连接处扭转刚度、机身弯曲刚度z向和y向、垂直尾翼弯曲刚度x向、垂直尾翼扭转刚度、机翼弯曲刚度x向和z向、机翼水平刚性单元长度、两边小翼弯曲刚度、垂直尾翼刚性单元长度、机翼对机身垂直偏置距离、机翼扭转刚度.

4.2 参数筛选及响应面有效性评价

对GARTEUR模型的初选参数进行F值检验，获得12个参数对10阶模态频率的显著性P值，如图7所示.

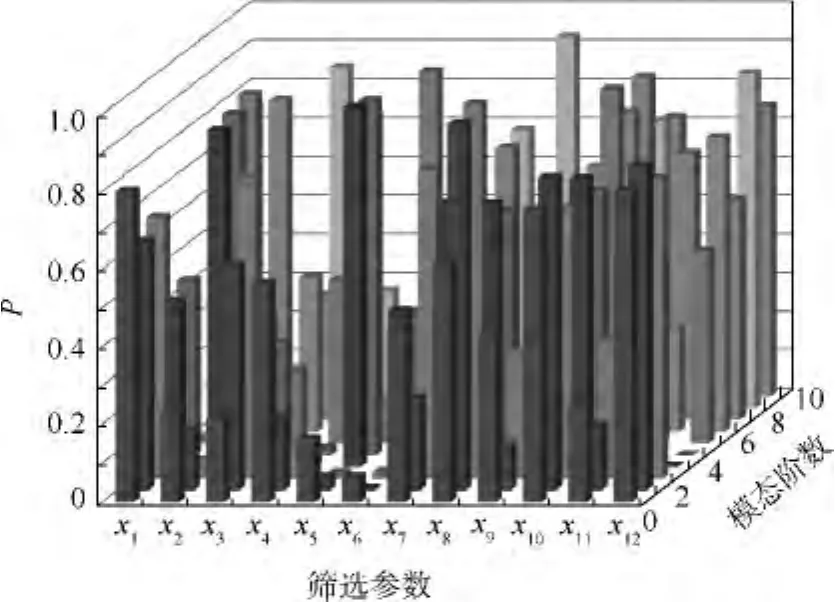
图7 12个初选参数的显著性P值

设定P=0.05为显著性水平临界值，从初始模型的x1～x12的12个参数中筛选出7个对各阶模态频率显著性的参数，如表2所示.将筛选出的7个显著参数构建响应面模型，响应面检验结果如图8所示，其均方根误差相对值和决定系数分别趋向0和1，准确地描述了GARTEUR结构参数与响应的关系.

表2 筛选出的显著性参数及修正前后变化

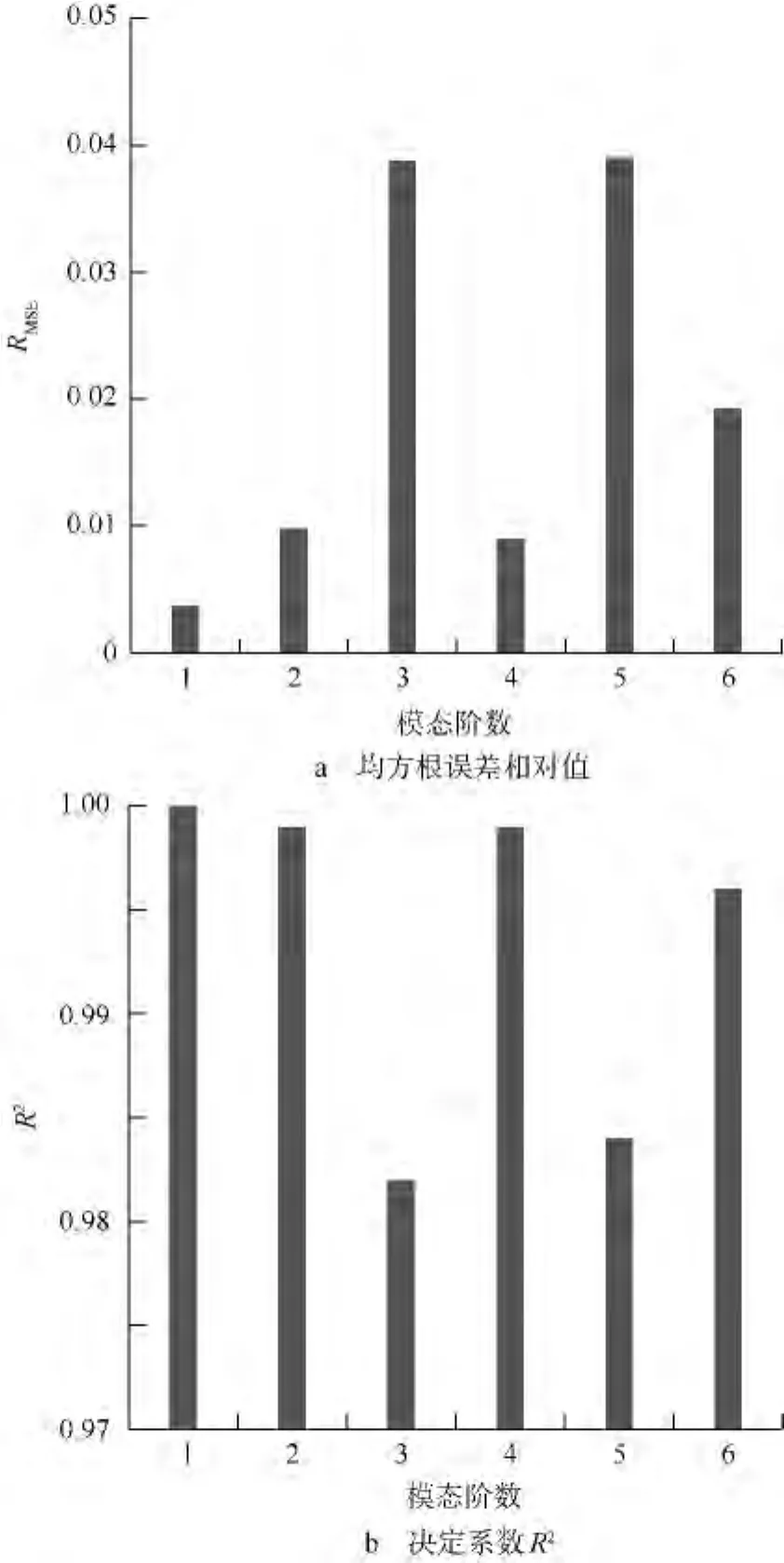
图8 GARTEUR模型的响应面有效性评价

4.3 响应面优化的模型修正结果

验证修正的模型是否具有一定的普适性，需检验修正模型复现及预示能力，高质量的修正模型应达到三级预示水平[14]:

1)能够精确复现参与修正频段内的试验数据;

2)能够准确预测参与修正频段外的试验数据;

3)对结构局部修改，模型不重新修正只需相应的改动就能预测结构修改后的动力学特性.

以文献[14]试验测试数据为参考，选取前6阶模态频率作为修正频段并构造目标函数(一级检验)，将模型修正转化为优化算法寻优的问题，如式(11)所示.后4阶模态频率作为预测频段，用于修正模型的二级预测检验.对构建的响应面模型采用遗传算法进行优化，获得参数最优解，代入有限元模型得到修正频率.GARTEUR模型的目标函数迭代收敛曲线，如图9所示.

图9 GARTEUR模型目标函数收敛曲线

模型修正前后的有限元分析结果和实测10阶模态频率值，如表3所示.

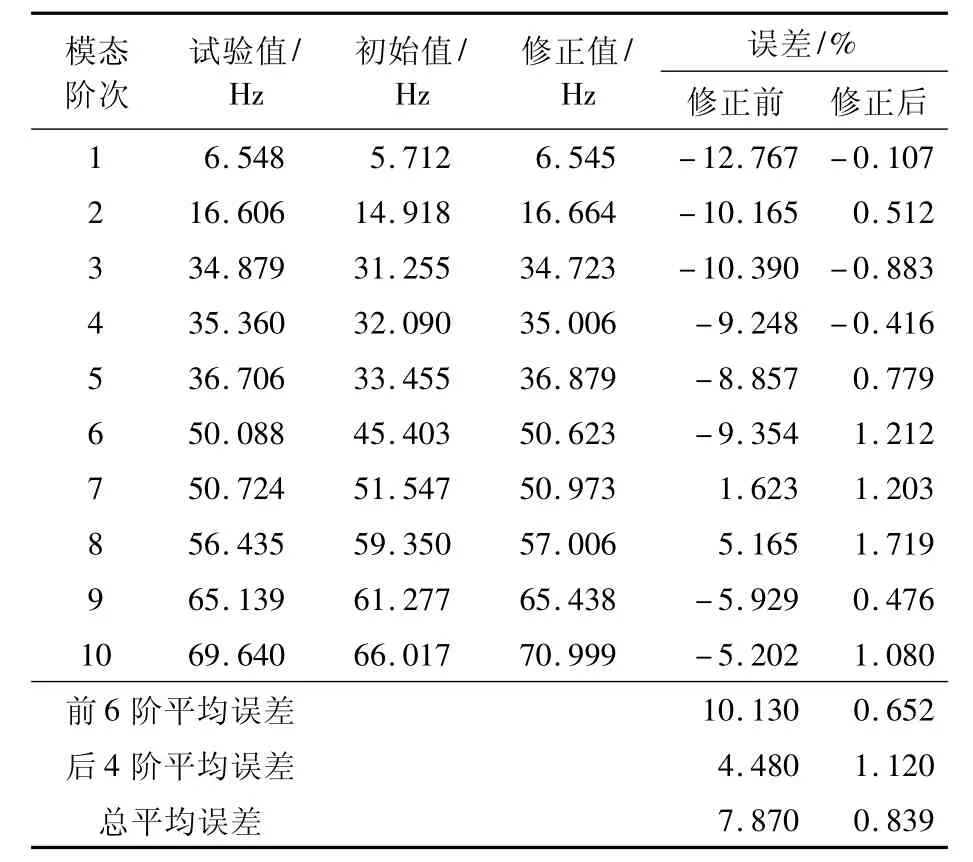
表3 GARTEUR模型的模态频率修正结果及误差对比

修正频段内的前6阶模态频率的平均误差由修正前10.13%降低到0.652%;预测频段内的后4阶模态频率的平均误差由4.48%降低到1.12%;总平均误差由7.87%降低到0.839%.可见，修正后有限元模型不但能复现修正频段的频率而且还能准确预测修正频段外的频率，满足一级和二级预测标准.

4.4 模型结构修改的预测性检验

将GARTEUR模型局部修改，如图6所示.机翼尖上的配重由0.15 kg改为0.72 kg，考察修正模型对局部结构修改后模态特性预测能力(三级预测)[14]，分析预测结果与实测模态频率对比，如表4所示.

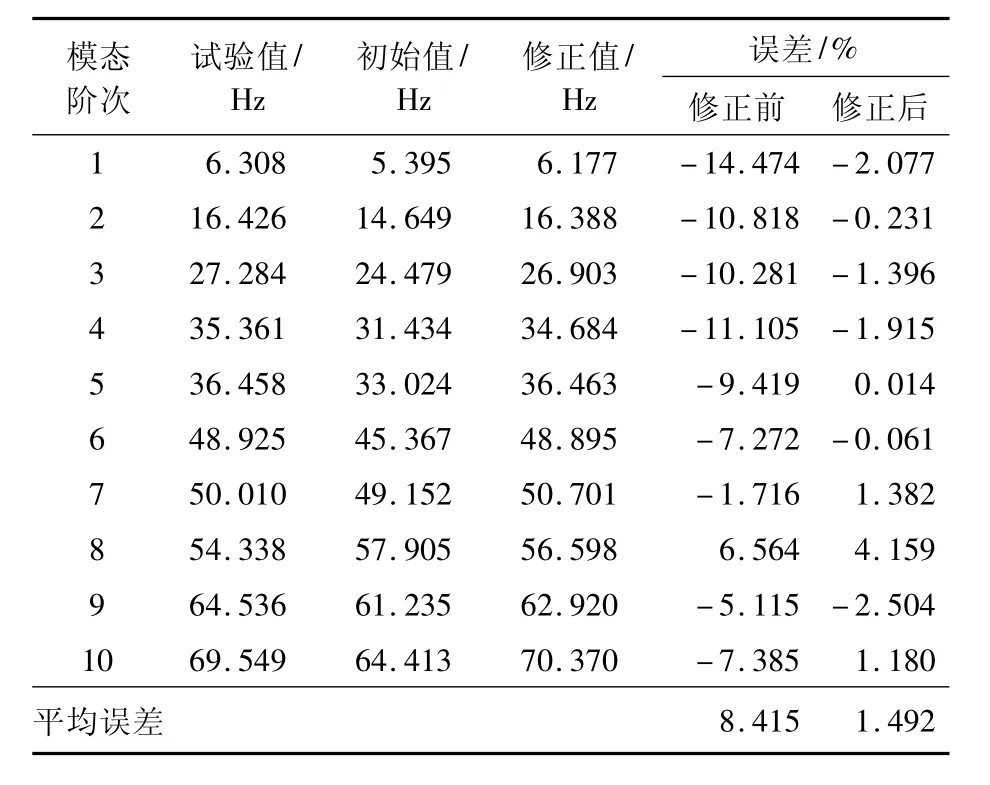
表4 GARTEUR模型局部修改后的频率预测结果及误差对比

相对于初始有限元模型，修正后模型的预测频率平均误差从8.415%降低到1.492%，预测结果的最大误差从初始模型的14.474%降低到2.077%，最小误差从1.716%降低到1.382%，表明修正模型的三级预测有效性.响应面优化后的修正模型不仅是具有试验数据复现能力的等效模型，还能基本反映结构的真实动态特性，模型具有一定普遍适用性.

5 结论

1)以优化拉丁方试验设计样本点，F值检验筛选修正参数来构造不完全4阶多项式响应面，最小二乘法确定多项式系数的方法建立的响应面能够代替有限元模型进行模型修正，避免修正过程中有限元模型的多次迭代，提高了分析效率.

2)三自由度系统的3种不同工况模型修正结果表明，待修正模型中有参数不存在或者有误差的情况下，响应面优化的模型修正也能得到准确的模态频率修正值，具有良好的模型修正能力.

3)通过F值检验筛选出GARTEUR模型对模态频率显著的参数来构造响应面进行修正.结果表明修正模型满足三级预示水平，即修正频段和预测频段具有良好的复现和预测能力，还能预测结构局部修改后的频率.修正模型具有一定的普遍适用性，验证了经过参数筛选后响应面优化的模型修正有效性.

References)

[1]丁继锋，韩增尧，马兴瑞.航天器动力学模型试验验证技术研究进展[J].力学进展，2012，42(4):395－405

Ding Jifeng，Han Zengyao，Ma Xingrui.Research evolution on the test verification of spacecraft dynamic model[J].Advances in Mechanics，2012，42(4):395 － 405(in Chinese)

[2]Xiong Y，Chen W，Tsui K L，et al.A better understanding of model updating strategies invalidating engineering models[J].Computer Methods in Applied Mechanics and Engineering，2009，198(15/16):1327 －1337

[3]张保强，陈国平，郭勤涛.基于模态频率和有效质量的有限元模型修正[J].振动与冲击，2012，31(24):69 －73

Zhang Baoqiang，Chen Guoping，Guo Qintao.Finite element model updating based on modal frequency and effective modal mass[J].Journal of Vibration and Shock，2012，31(24):69 －73(in Chinese)

[4]王永华，杨欣毅，苏珉，等.熵判别粒子群优化算法在发动机模型修正中的应用[J].航空动力学报，2013，28(1):74 －81

Wang Yonghua，Yang Xinyi，Su Min，et al.Engine model correction based on entropy criterion PSO[J].Journal of Aerospace Power，2013，28(1):74 －81(in Chinese)

[5]Coppotelli G，Rinaldi R，Crema L B.Structural updating of the VEGA－UCMEC FE model using vibration test data[R].AIAA－2008－1850，2008

[6]Davoodi M R，Amiri J V，Gholampour S，et al.Determination of nonlinear behavior of a ball joint system by model updating[J].Journal of Constructional Steel Research，2012，71:52 －62

[7]Mthembu L，Marwala T，Friswell M I，et al.Finite element model selection using particle swarm optimization[C]//Conference Proceedings of the Society for Experimental Mechanics Series.New York:Springer，2011，4:41 －52

[8]Jin R C，Chen W，Sudjianto A.An efficient algorithm for constructing optimal design of computer experiments[J].Journal of Statistical Planning and Inference，2005，134(1):268 －287

[9]Khuri A I，Mukhopadhyay S.Response surface methodology[J].WIREs Computational Statistics，2010，2(2):128 － 149

[10]Rice J A.Mathematical statistics and data analysis[M].3rd ed.Florence:Brooks Cole，2007

[11]Mares C，Mottershead J E，Friswell M I.Stochastic model updating:part1theory and simulated example[J].Mechanical Systems and Signal Processing，2006，20(7):1674 －1695

[12]Kozak M T，Öztürk M，Özgüven H N.A method in model updating using miscorrelation index sensitivity[J].Mechanical Systems and Signal Processing，2009，23(6):1747 －1758

[13]D’Ambrogio W，Fregolent A.Dynamic model updating using virtual antiresonances[J].Shock and Vibration，2004，11(3/4):351－363

[14]Link M，Friswell M I.Working group 1:generation of validated structural dynamic models－results of a benchmark study utilizing the CARTEUR SM－AG19 test－bed[J].Mechanical Systems and Signal Processing，2003，17(1):9 －20