基于T-H方程的多脉冲最优交会方法

姬晓琴

(宇航智能控制技术国家级重点实验室，北京100854)

肖利红 陈文辉

(北京航天自动控制研究所，北京100854)

交会是指两个或两个以上的飞行器在空间轨道上按预定位置和时间相会[1].由于在常推力下研究轨道转移问题相当复杂，在空间任务的初步分析和设计时，常假设发动机按脉冲方式工作.

1960年，Clohessy等[2]推导出了基于目标轨道坐标系的线性化相对运动方程，即C-W方程，该方程有解析解，因此被广泛应用于研究邻近的近圆轨道上的交会问题.同时期Lawden[3]提出的主矢量法也是比较典型的方法，给出了最优脉冲交会的必要条件.Handelsman等[4]把主矢量概念推广到非最优飞行轨道，提出了一种冲量(脉冲)校正理论.针对椭圆参考轨道，Lawden[5]和 Hempel等[6]以真近点角为自变量给出了椭圆参考轨道相对运动的非线性状态方程，即T-H方程，并导出了方程的解析解，但解有奇异性且形式较为复杂;2002年，Yamanaka等[7]给出了T-H方程的状态转移矩阵，形式简单且解无奇异性，为研究椭圆参考轨道的多脉冲交会策略提供了方便.Carter等[8－11]对椭圆及圆参考轨道均进行了较为深入的研究.谌颖[12]研究了共面椭圆轨道上固定点的燃料最优交会和时间固定的最优交会.杨乐平等[13]研究了基于导航点的及基于随机优化的多脉冲交会方法.

现在，基于牛顿平方反比引力场中的脉冲交会问题，已有比较成熟的结论，但是研究引力摄动情况下的脉冲交会问题的文献较少，还有待于继续研究.荆武兴等[14]研究了椭圆参考轨道上的最优精确交会，考虑J2摄动时，在求得双脉冲优化解后，基于轨道积分进行终端状态预测，采用迭代方法确定脉冲的增量，因此耗时较长.宋旭民等[15]研究了基于改进的 Lambert法的多脉冲规划方法，采用轨道积分进行脉冲间的状态预测.谭丽芬[16]研究了考虑J2摄动的时间固定单脉冲多圈Lambert最优交会，方法与前者相似.Gim等[17]导出了考虑J2摄动及椭圆轨道的相对运动的状态转移阵，长期预测精度较高，但只适用于近距离的相对运动.

本文针对椭圆参考轨道，基于T-H方程进行多脉冲轨迹优化研究，建立了时间固定燃料最省的优化模型，优化参数为脉冲及脉冲施加时刻.针对J2摄动或航天器初始相对距离较大时，T-H方程的线性化误差一般不容忽略，提出了一种新的节点状态预测方法，即采用前一优化节点的状态导出的轨道根数推导当前节点的状态.因无需轨道积分，加快了优化收敛速度.用优化的多脉冲解进行轨道数值积分以验证终端精度，仿真结果表明，即使在考虑J2摄动时，终端状态的精度仍然较高.

1 T-H方程

这里直接给出以真近点角f为自变量的方程组，即通常所说的T-H方程.

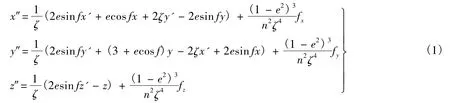
式中，e为轨道偏心率;n为轨道平均角速率;ζ=1+ecosf;fx，fy，fz为飞行器所受的摄动力和控制力引起的加速度之和.

一般情况下难以得到T-H方程的解析解.但是若假设飞行器不施加控制且忽略各种摄动的影响，作变量变换:，经推导可得到 T-H 方程的齐次解析解[1，7]:

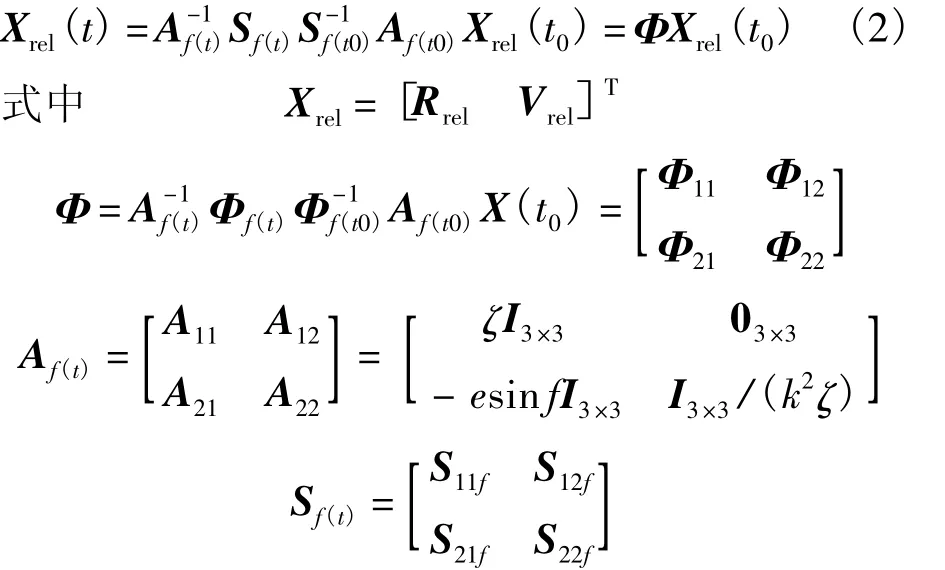
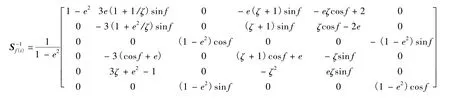
2 N-脉冲最优交会方法

N-脉冲最优变轨问题可描述为:给定起始时间t0及初始状态X0=[R0V0]T，期望在 tf时刻转移到终端状态Xf=[RfVf]T，求如何施加N次脉冲使得能量最省，其中T表示转置.

假设在时间tk(k=1，2，…，N)处施加脉冲速度增量为 ΔVk，令 Δtk表示 t0，tk，tf各时间节点的间隔，则根据T-H方程可知脉冲施加前后的状态为

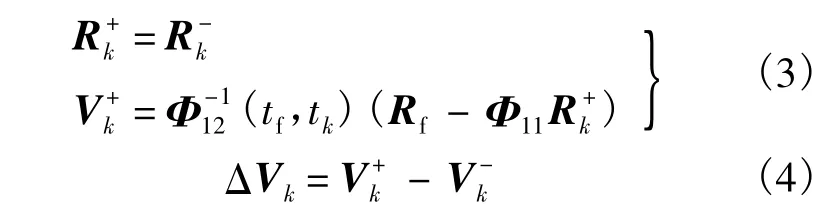
因为T-H方程是线性化一阶近似模型，存在模型误差，所以需寻求一种求解预测值，的方法.一种预测方法是基于数值积分方法进行预测，但该方法耗时较长，不太适合星上实时应用.这里给出一种基于轨道参数进行预测的方法，因无需轨道积分，故耗时较少;又因为该预测方法是基于二体轨道模型给出的预测，无T-H方程的线性化误差，只包含有J2摄动引起的误差，因此预测精度较高.具体过程是:首先依据施加第k－1次脉冲时刻后的相对参数，，可得到航天器的位置、速度参数，由位置、速度参数可计算当时的轨道根数，然后根据轨道根数以及目标轨道根数预测施加第k次脉冲时刻前的.

则整个交会过程所需的总脉冲如下:

显然，ΔV是tk的函数，可对脉冲施加时刻进行优化.

综上可得多脉冲优化模型如下.

性能指标:

边界条件:

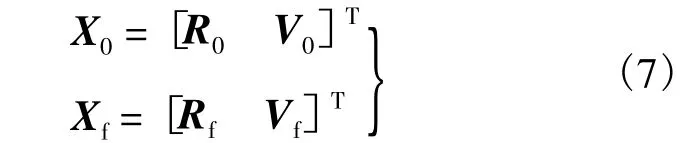
约束条件:

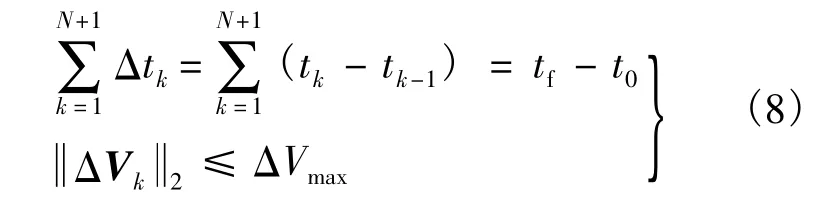
式中ΔVmax表示最大脉冲限制.

因上述优化模型的目标函数高度非线性，且约束条件既有线性等式约束，又有非线性不等式约束，可采用序列二次规划算法(SQP，Sequential Quadratic Programming)求解.

3 仿真分析

3.1 仿真条件

1)目标飞行器取为轨道高度600 km的太阳同步轨道，其轨道根数为:轨道半长轴 a=6971015 m，轨道偏心率 e=0.01，轨道倾角 i=97.76°，轨道近地点幅角 ω =30°，轨道真近地点角f0=30°，轨道升交点赤经Ω=60°.

2)追踪飞行器与目标飞行器的初始相对状态参数为

要求的终端状态参数为

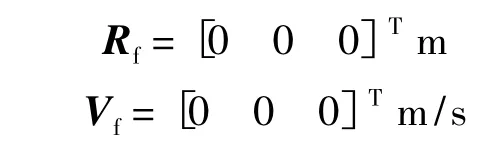
3)转移时间为2/3个目标飞行器轨道周期.

3.2 仿真结果及分析

采用前述的多脉冲优化模型，进行多脉冲最优交会方法仿真研究.应用matlab中的fmincon函数进行优化，优化的能耗(速度增量)随脉冲次数的变化如图1所示.从图中可看出，随着脉冲次数N的增加，能耗逐渐趋于稳定值.

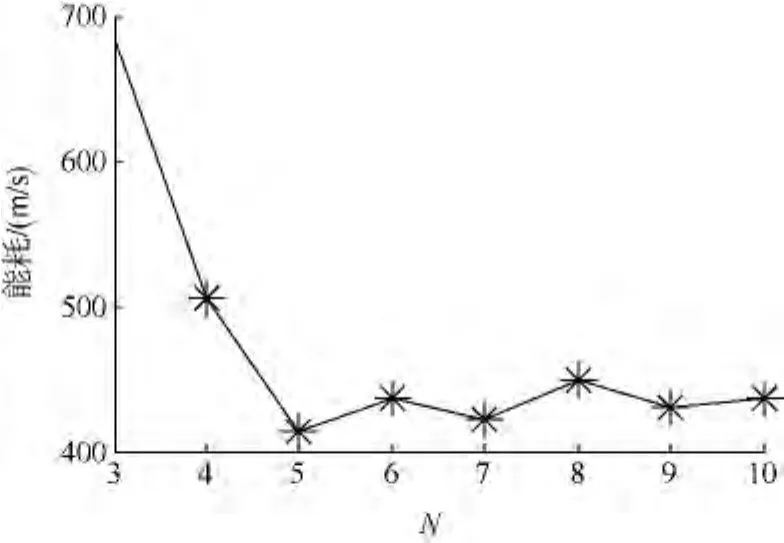
图1 能量消耗随脉冲次数的变化

采用精确的动力学模型，进行轨道数值积分至转移时间结束，以验证多脉冲最优交会方法的终端位置精度.由于T-H方程为线性化一阶近似模型，即使不考虑J2摄动时，也存在线性化误差，故直接采用优化的脉冲进行积分，终端误差较大.本文采用在优化的脉冲施加时刻利用T-H方程在线求取最优双脉冲交会所需速度增量的方法，来减小终端误差.

图2给出了N=6时脉冲优化的轨迹，同时给出了考虑J2摄动与不考虑J2摄动的数值积分轨迹曲线.

为清晰起见，图3给出了施加第5次脉冲前后的局部轨迹.从图中可看出，优化轨迹与数值积分轨迹几乎重合，说明了N-脉冲优化方法优化的轨迹精度比较高.

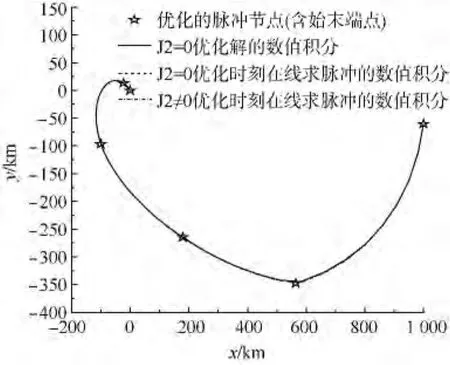
图2 N=6脉冲优化轨迹及数值积分轨迹

取N=3～10，当J2=0和J2≠0时，终端时刻未施加脉冲时的终端状态参数分别如表1、表2所示.可见，前者终端位置精度优于10 m，后者优于75 m.另外，若J2=0，采用优化解直接进行数值积分与在线求取速度增量进行数值积分相比，优化的能耗与实际的能耗趋于一致，两者相差不到0.2m/s，而终端位置精度大幅提高.以N=6为例，前者的终端位置精度为70 m，能耗为435.54m/s，后者的位置精度为2.0m，能耗为435.51 m/s，两者能耗几乎一致，而位置精度提高了一个数量级，这表明了在线求取脉冲增量的有效性.若J2≠0，随着脉冲数的增加，当N＞5时，优化的能耗与实际的能耗趋于一致，两者相差不到3m/s.

为进一步验证所提算法的正确性和有效性，取虚拟目标卫星为轨道高度1000 km的太阳同步轨道，将偏心率加大，e=0.1，i=99.26°，其他参数同前，进行仿真运算.仿真结果再次表明了该方法的有效性:J2=0时终端位置精度仍优于10 m;J2≠0时终端位置精度优于60 m.

图3 N=6脉冲优化轨迹及数值积分轨迹(局部)

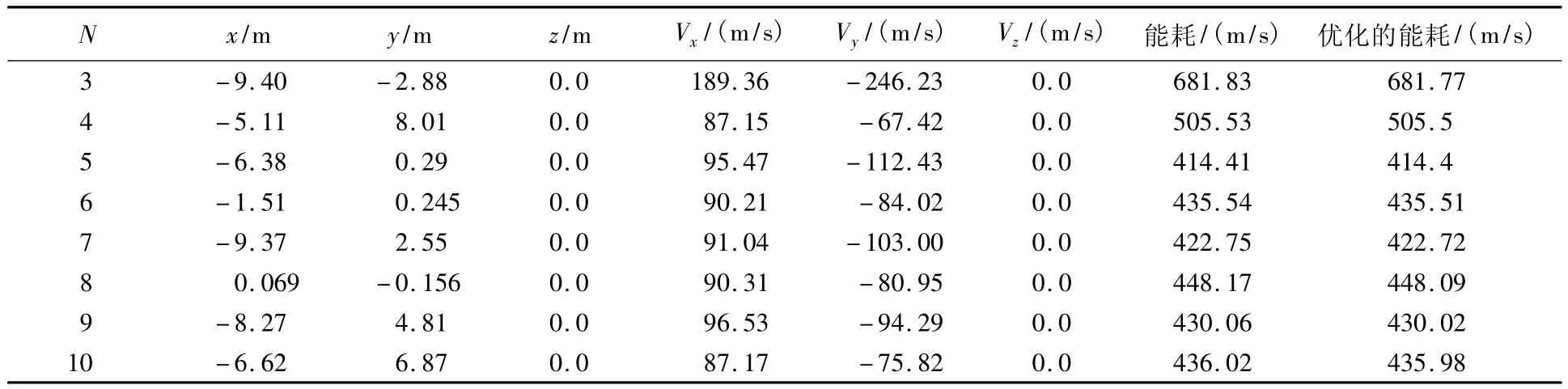
表1 终端速度有约束的终端状态J2=0

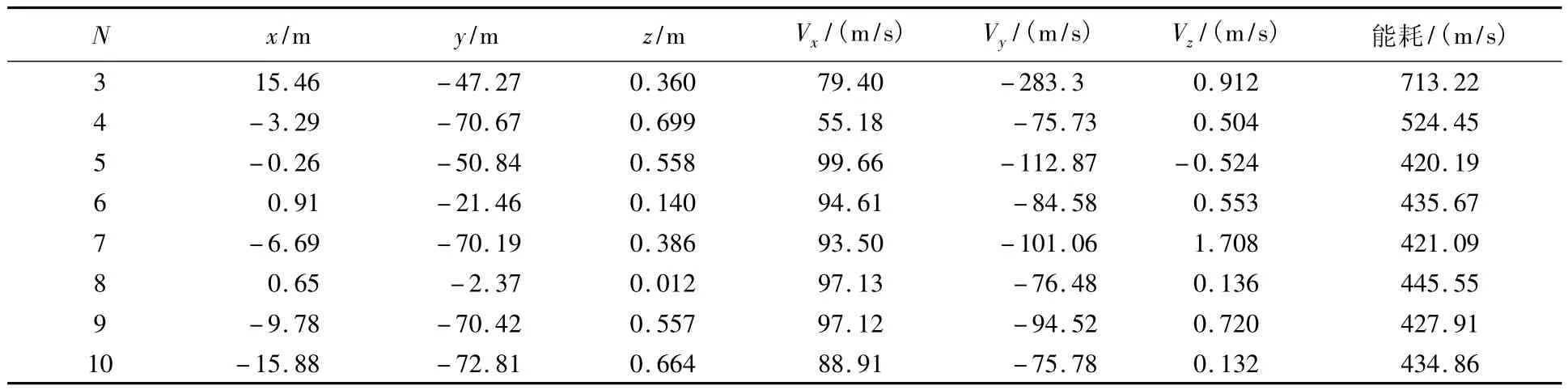
表2 终端速度有约束的终端状态J2≠0

4 结论

针对椭圆参考轨道，提出了一种基于T-H方程的N-脉冲最优交会方法，建立了时间固定燃料最省的优化模型，优化参数为脉冲及脉冲施加时刻.数学仿真结果表明:

1)N-脉冲优化过程中，应用本文提出的节点状态预测方法，即采用前一优化节点的状态导出的轨道根数推导当前节点的状态，因无需轨道积分，故有效提高了优化收敛速度.

2)N-脉冲优化方法优化的轨迹精度较高.若采用在优化的时刻利用T-H方程在线求取最优双脉冲轨道转移所需速度增量的方法，可进一步提高终端位置精度.

3)当考虑到J2摄动，且航天器初始相对距离较大时(约1 000 km)，该优化方法的终端位置精度仍然较高，达到75 m.

References)

[1]林来兴.空间交会对接技术[M].北京:国防工业出版社，1995:1

Lin Laixing.Space rendezvous and docking technology[M].Beijing:National Defence Industry Press，1995:1(in Chinese)

[2]Clohessy W H，Wiltshire R S.Terminal guidance system for satellite rendezvous[J].Journal of Aerospace Science，1960，27(9):653－658

[3]Lawden D F.Optimal trajectories for space navigation[M].London:Butterworths，1963

[4]Handelsman M，Lion P M.Primer vector on fixed-time impulse trajectories[J].AIAA Journal，1968，6(1):127 － 132

[5]Lawden D F.Fundamentals of space navigation[J].Journal of the British Interplanetary Society，1954，13(2):87 －101

[6]Tschauner J，Hempel P.Rendezvous zu einem in elliptischer bahn umlaufenden ziel[J].Astronautica Acta，1965，11(2):104－109

[7]Yamanaka k，Ankersen F.New state transition matrix for relative motion on an arbitrary elliptical orbit[J].Journal of Guidance，Control，and Dynamics，2002，25(1):60 －66

[8]Carter T，Humi M.Fuel-optimal rendezvous near a point in general Keplerian orbit[J].Journal of Guidance，Control，and Dynamics，1987，10(6):567 －573

[9]Carter T.New form for the optimal rendezvous equations near a Keplerian orbit[J].Journal of Guidance，Control，and Dynamics，1990，13(1):183 －186

[10]Carter T，Alvarez S A.Quadratic-based computation of four-impulse optimal rendezvous near circular orbit[J].Journal of Guidance，Control，and Dynamical Astronomy，2003，23(1):109－117

[11]Carter T，Humi M.A new approach to impulse rendezvous near circular orbit[J].Celestial Mechanics and Dynamical Astronomy，2012，112(4):385 －426

[12]谌颖.空间最优交会控制理论与方法研究[D].哈尔滨:哈尔滨工业大学，1992

Chen Ying.Space optimal rendezvous control theory and methods[D].Harbin:Harbin Institute of Technology，1992(in Chinese)

[13]杨乐平，朱彦伟，黄涣.航天器相对运动轨迹规划与控制[M].北京:国防工业出版社，2010:110－124

Yang Leping，Zhu Yanwei，Huang Huan.Spacecraft relative motion trajectory planning and control[M].Beijing:National Defence Industry Press，2010:110 －124(in Chinese)

[14]荆武兴，陈伟跃.摄动椭圆参考轨道上的最优精确交会[J].中国空间科学技术，2011，31(2):16 －24

Jing Wuxing，Chen Weiyue.Fuel-optimal precise rendezvous guidance law in elliptical reference orbit with J2 perturbation[J].Chinese Space Science and Technology，2011，31(2):16－24(in Chinese)

[15]宋旭民，范丽，陈勇.考虑轨道摄动影响的多冲量交会规划方法研究[J].航天控制，2011，29(4):71 －74

Song Xumin，Fan Li，Chen Yong.The research on the multi-impulse rendezvous trajectory planning with orbit perturbation[J].Aerospace Control，2011，29(4):71 －74(in Chinese)

[16]谭丽芬.赤道椭圆交会轨道规划与制导方法[D].长沙:国防科学技术大学，2011

Tan Lifen.Rendezvous trajectory planning and guidance approach for equatorial elliptical orbit[D].Changsha:National U-niversity of Defense Technology，2011(in Chinese)

[17]Gim D W，Alfriend K T.State transition matrix of relative motion for the perturbed non circular reference orbit[J].Journal of Guidance，Control，and Dynamics，2003，26(6):956 －971