广义I型逐阶区间删失混合Weibull数据的参数估计
2014-11-03苑延华
苑延华
(黑龙江科技大学 理学院, 哈尔滨 150022)
广义I型逐阶区间删失混合Weibull数据的参数估计
苑延华
(黑龙江科技大学 理学院, 哈尔滨 150022)
源于有限混合总体的广义I型逐阶区间删失数据参数估计方法的研究不多,基于有限混合Weibull模型,讨论Expectation-Maximization(EM)算法对广义I型逐阶区间删失数据参数估计的有效性及其改进。首先给出估计参数的EM算法,通过仿真算例,说明EM算法对广义I型逐阶区间删失混合数据参数估计产生了过度迭代现象,进而,提出了停止EM算法的加权绝对偏差信息准则。改进的EM算法改善了EM算法无法确定参数估计停止迭代时刻的不足,在选择适当初值后,可快速获得满意的参数估计结果。仿真算例验证了该方法的有效性。
广义I型逐阶区间删失; 加权绝对偏差信息; 有限混合Weibull分布; EM算法
0 引 言
I型删失、II型删失和逐阶删失是工业寿命检验和医疗生存分析中最常见的删失方案,文中,考虑与I型逐阶区间删失[1-2](Progressive Type-I Interval Censoring)不同的广义I型逐阶区间删失数据并假设个体寿命服从两组分五参数混合Weibull分布。
在可靠性分析或寿命分析领域中,带有逐阶删失的混合分布模型正吸引越来越多的研究者的关注与研究,取得了一些卓越的成果。文献[1-9]主要从单一分布总体的角度考虑了总体分布参数的估计问题,常用参数估计的方法为最大似然估计、贝叶斯估计等方法。如E. B. Mokhtari等[3]用最大似然估计和渐近最大似然估计法讨论了带有II型逐阶混合删失的Weibull分布的参数估计。而文献[10-15]主要讨论了关于混合分布参数的最大似然、EM算法等估计方法。如C. T. Lin等[10]用最大似然和贝叶斯估计法研究了I型自适应逐阶混合删失Weibull分布的参数估计。受这些研究的启发,笔者研究广义I型逐阶区间删失混合Weibull分布下,参数最大似然估计EM算法的有效性问题,这个主题国内外研究者鲜有触及。
1 删失数据的定义
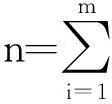
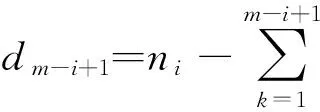

图1 I型逐阶区间删失数据的观测方案

图2 广义I型逐阶区间删失数据的观测方案
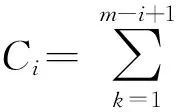
称这样的数据是广义I型逐阶区间删失的,主要有两个原因:

(2)补充数据Ri=di可以理解为iΔ处随机删失的个体数目。
这样,文中所定义的广义I型逐阶区间删失数据就是文献[1]所定义的I型逐阶删失数据的一个特殊类型。事实上,广义I型逐阶区间删失数据大量地存在于跟踪调查等实用场合,对此类数据的有效统计分析具有很强的实用价值。
2 有限混合Weibull分布模型
2.1两组分混合Weibull分布
N组分有限混合Weibull分布模型[16]的概率密度函数和分布函数分别是
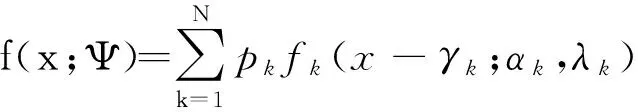
(1)
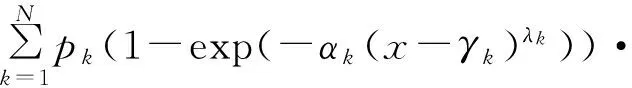
I[0,+∞)(x-γk),
其中,fk(x-γk;αk,λk)=αkλkxλk-1exp(-αk(x-γk)λk)I[0,+∞)(x-γk),αk>0,λk>0,IA(x)是集合A的示性函数,即当x∈A时IA(x)=1,否则IA(x)=0。于是,记Ψ=(p1,…,pN-1,α1,λ1,γ1,…,αN,λN,γN)T,参数θk=(αk,λk,γk)T表示第k(k=1,2,…,N)个子总体(组分)的参数,p=(p1,p2,…,pN)T是混合比,满足

称随机变量X服从N组分3N-1参数(即Ψ)混合Weibull分布,若其概率密度函数满足式(1),记作X~FMWeib(x|Ψ;N)。
则随机变量X~FMWeib(x|Ψ;N)的幸存函数为

其中sk(x)=exp(-αk(x-γk)λk)·I[0,+∞)(x-γk),k=1,2,…,N。
文中余下部分规定参数N=2,γk=0(k=1,2),即随机变量X服从两组分混合Weibull分布,比值p表示第一子总体的占比,将其记作

(2)
从图3可见混合Weibull分布能够描述比较复杂的随机特性,在图中所给参数下,这一混合总体的风险率呈现出了先降后升再降的先高后低的变化特征,说明混合Weibull分布具有较好的灵活性,适合描述复杂场合的寿命规律,这也是对其研究感兴趣的一个重要原因。

图3 混合Weibull分布0.7,0.08,0.5,0.5,2;2)的幸存函数、概率密度函数和风险函数
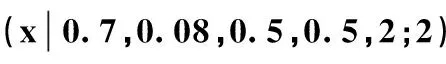
2.2完全数据的似然函数
设观测的n个个体X1,X2,…,Xn寿命独立同分布(2),即

并设示性向量Ij=(Ij1,Ij2)T∈2×1,Ij的两个分量中有且只有一个是1,其余分量均为0,即Ijk=1表示Xj来自混合总体中的第k(k=1,2)个子总体,否则Ijk=0。记I=(I11,I12,I21,I22,…,In1,In2)T∈n×2,则矩阵I表示所有被观察个体寿命X1,X2,…,Xn的分类示性矩阵,于是,完全数据Z={Zj}={j=1,2,…,n}的似然函数为
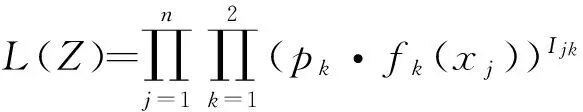
(3)
2.3广义I型逐阶区间删失数据的似然函数
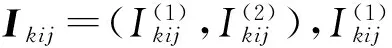
用X=(Xj)表示所有个体的寿命组成的向量,I=(I1,I2,…,In)T∈n×4m表示示性单元矩阵,其中的第j行给出了Xj的属性特征,C={C1,C2,…,Cm}表示观测区间内失效的个体数目,D={R1,R2,…,Rm}表示从每个观测区间右端点随机删失的个体数目。于是Z={Zj}={X,I,C,D}为与Y={C1,C2,…,Cm,R}对应的完全数据,这里R=R1+R2+…+Rm,并且完全数据Zj={Xj,Ij,Ci,Di}的概率密度函数为

再由式(3)可得广义I型逐阶区间删失补全后的完全数据Z所对应的对数似然函数为

(logpk+logfk(xj))。
(4)


(5)
在下一部分里,讨论已知不完全数据Y的情况下,参数Ψ的最大似然估计的EM算法。
3 基于EM算法参数Ψ的最大似然估计

3.1模型基本假设与性质
根据引言中广义I型逐阶区间删失数据的表述,可知文中所研究模型满足以下三个基本假设,这些假设与实际观察的环境条件是相统一的。
假设1观察时间区间等间隔。
假设2每个时间节点进入观测的个体数目独立服从同分布。
假设3文中讨论的广义I型逐阶区间删失数据依据图2所示方案获得。
基于以上假设,设与不完全观测数据Y={C1,C2,…,Cm,R}对应的完全数据为Z={X,I,C,D},C={C1,C2,…,Cm},D={R1,R2,…,Rm},i=1,2,…,m,I=(I1,I2,…,In)T∈n×4m,有如下性质成立。
性质1区间失效数据C服从多项式分布,满足

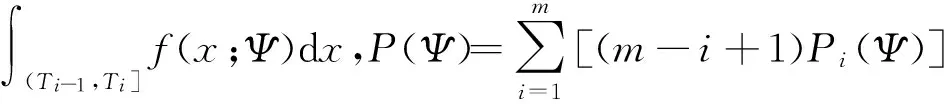
性质2删失数据D服从多项式分布,满足
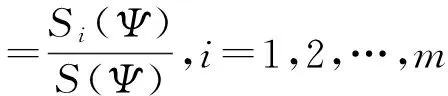

3.2基于EM算法参数Ψ的最大似然估计
在两组分混合Weibull分布及广义I型逐阶区间删失假设下,讨论在EM算法的框架下求解参数Ψ=(p,α1,λ1,α2,λ2)的最大似然估计问题。
设定初始值Ψ(0),根据式(5),EM算法的第t次迭代为:
E步假定参数的第t-1次迭代估计为Ψ(t-1),则第t步的Q函数为
Q(Ψ;Ψ(t-1))=EΨ(t-1)[logLc(Z;Ψ)|Y]=

(6)
这里k=1,2,记p1=p,p2=1-p,于是

(7)
其中


另一方面,
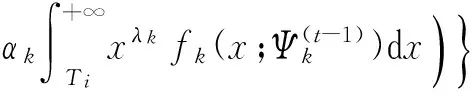
(8)
其中,





w=c1+c2+…+cm,

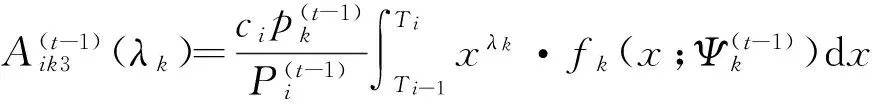
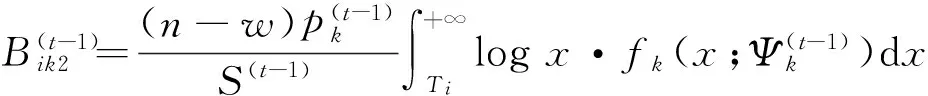

于是,根据式(7)和(8),式(6)的Q-函数可简记为
Q(Ψ;Ψ(t-1))=EΨ(t-1)[logLc(Ψ)|Y]=



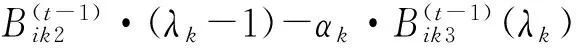
(9)
定理1Q-函数关于参数Ψ具有一阶连续偏导数。
Q-函数关于参数pk、αk一阶偏导存在且连续是显然的,这里不进行证明。
定义1若对任意正实数μ,随机变量Xμ的数学期望EXμ存在,则称随机变量X具有连续阶原点矩,或称随机分布具有连续阶原点矩。
引理1Weibull分布连续阶原点矩存在,且具有一阶连续可微性。
证明设随机变量X服从参数为α(>0),λ(>0)的Weibull分布,μ∈(0,+∞)为任意指定的正实数,则随机变量X的μ阶原点矩为


(10)
式(10)中第二个等号,是引进变换t=αxλ实现的,根据伽马函数Γ(s)(s>0)关于参数s具有任意阶连续导数的性质,以及复合函数的可导性,可知服从Weibull分布的随机变量具有任意阶的原点矩,且对阶次μ具有任意阶连续偏导数,则关于μ的一阶偏导为
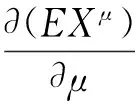
其中Γ′(·)表示Γ函数关于自变量·的导数。此外还有

成立。

M步对式(9)中Q-函数的参数Ψ求偏导,得如下方程组:
(11)
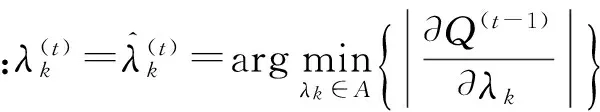
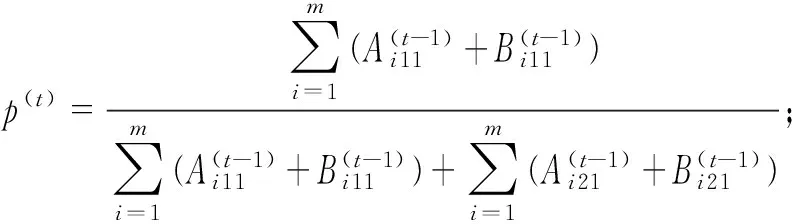
(12)
(Ⅱ)

(13)
其中,


3.3算例1
下面通过仿真算例说明EM算法的有效性。这里仿真数据生成方案如下:
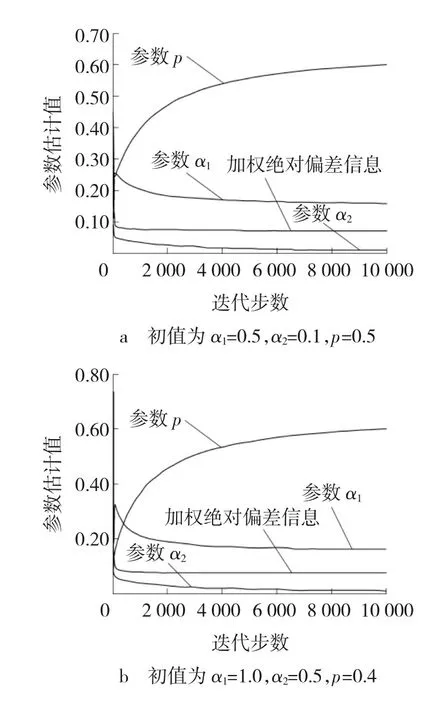
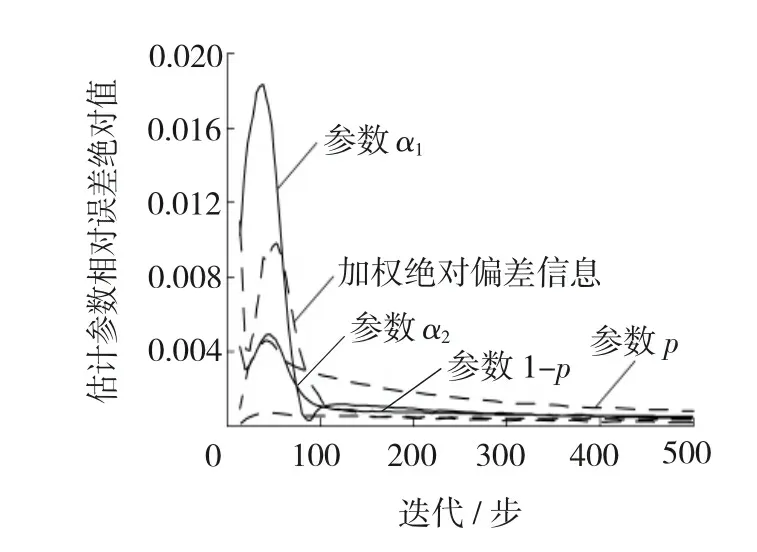
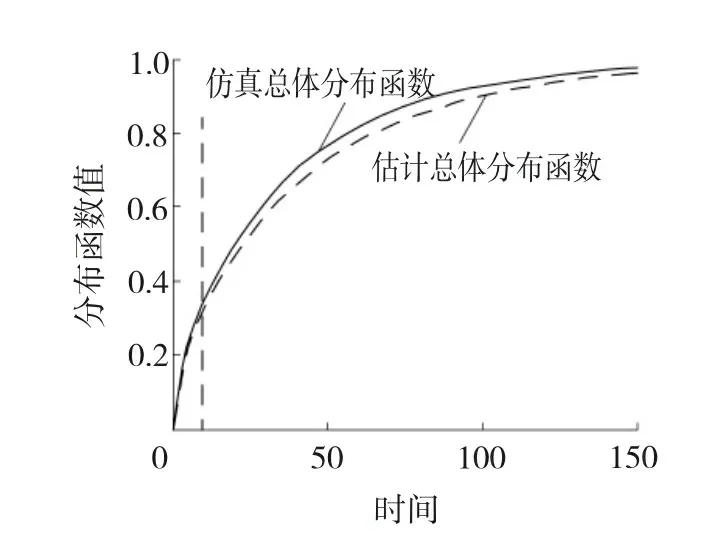
第1步,指定分组数m及观测时间点0 第2步,独立生成m组同泊松分布P(μ·Δ)的样本数据ni,i=1,2,…,m。 第3步,对于每个i按概率p生成长度为ni的1、0数据串,其中数字1表示该观测数据来自第一个子总体,数字0表示该观测数据来自第二个子总体,并记录该数据串中数字1的个数为ni1,数字0的个数为ni0,p为第一个子总体的混合比。 第4步,独立生成m组容量为ni1,i=1,2,…,m的服从Weibull分布f1(x;α1,λ1)的数据xi1j,i=1,2,…,m;j=1,2,…,ni1,再独立生成m组容量为ni0,i=1,2,…,m的服从Weibull分布f2(x;α2,λ2)的数据xi0k,i=1,2,…,m;k=1,2,…,ni0。 第5步,按照图2所示方法统计分组观测数据Y。 现在,考虑一个特别的算例。令λ1=λ2=1且已知,此时,仿真数据总体分布服从两组分混合指数分布,仿真总体的其他参数为α1=0.2、α2=0.04、p=0.3、m=10、μ=80、Δ=1,按此参数生成的时间区间i内的失效数据分别为60、66、45、24、25、17、10、6、5和2,其中,样本容量n=759,失效总数w=260,时间区间i表示观测区间((i-1)Δ,iΔ],这里Δ=1。图4给出了仿真总体的概率密度函数、生存函数和风险函数的图像,从中可见混合指数分布的风险函数不再是常数。现在基于上文仿真数据,根据式(12)、(13)进行参数估计。 图4 混合Exponential分布的幸存函数、概率密度函数和风险函数 图5显示了在不同初值情况下,EM算法参数的 图5 EM算法下参数估计值与迭代步数间的关系 估计的收敛特性,可以看到,不同初值产生的最终的收敛状况几乎没有差别;图6显示了200步之内的迭代,可见不同初值对估计结果在最初的计算中是有较大影响的。从图5和6还可发现,随着迭代步数的增加,混合比p越来越大,参数α1、α2尽管不同,却是越来越小,这说明以增加迭代步数为代价获得更好估计结果是不合适的。 图6 200步以内不同初值EM算法的收敛效果 产生这一现象的原因在于文中所提的广义I型逐阶区间删失数据自身没能提供分类信息,而从图6的细节上会发现参数p的估值都有一个先降后升的过程,即p的估计值有最小值;另一方面,对基于有限混合模型的广义I型逐阶区间删失数据估计的一个重要兴趣在于:希望知道短寿子总体的寿命分布信息和占比,这促使提出第4部分所描述的基于加权绝对偏差信息准则的改进EM算法,图5和6也显示了加权偏差信息准则的良好收敛特性。 4.1改进的EM算法 实际上,在质量监控领域中,对于广义I型逐阶区间删失统计数据的兴趣在于早期发现质量问题,以便实施质量控制。因此,在参数估计中,希望知道混合比p的合理的最小估值、短寿子总体寿命的合理最短估值。这种观点是基于这样的事实:短寿命子总体的最小占比值的估值代表着人们最乐观的估计,当它都不可接受时,糟糕的情形就更危险了,所以,它适于作为风险评估的指标;另外,在EM算法估计的不断迭代中寿命参数不断变小,意味着子总体平均寿命的延长,所以希望知道子总体寿命的最短估计值。基于这样的事实,文中提出基于加权绝对偏差信息准则的改进EM算法对参数进行估计。 首先定义加权绝对偏差信息,并将其作为EM算法的终止准则。 定义2在有限混合Weibull分布情形下,对于文中所提的广义I型逐阶区间删失数据,定义加权绝对偏差信息(WeightedAbsoluteDeviationInformation,WADI)为μ,即 其中区间失效数据Ci及其分布满足性质1。 假设4在观测时间内,来自短寿命子总体的个体几乎都发生失效;一般长寿命子总体的平均寿命是短寿命子总体平均寿命的三倍以上。 基于加权绝对偏差信息准则的EM算法: 第2步,加权绝对偏差信息准则(WADIC)为以加权绝对偏差信息的相对误差绝对值小于指定阀值为迭代终止条件。 第3步,实施EM算法的估计,重复迭代,直到获得可接受的估计结果。 4.2算例2(算例1续) 图7 迭代步数与各被估参数相对误差绝对值的关系 图8 估计分布函数的拟合效果与迭代步数的关系 4.3算例3 (iii)比较这十三个估计值,选出μ最小的矩形,作为下一步迭代时搜索参数估计值的区域。 重复(i)~(iii)步,直到这些嵌套区域内估计总体的μ的相对误差绝对值小于阀值0.000 1停止迭代,从而获得参数λ1、λ2、p、α1、α2的估计值。 经过迭代计算,得到参数估计值分别为α1=0.188 4、α2=0.035 0、p=0.112 3、λ1=1.798 25、λ2=0.898 3。图9给出了仿真总体的概率密度函数和估计总体概率密度函数的对比图,可见所提算法对观测数据的拟合效果较好,这种搜索定位法节约计算资源,使得估计运算的效率较高。 图9 仿真总体和估计总体的概率分布函数 文中讨论了两组分混合Weibull分布在广义I型逐阶区间删失情形下参数估计的EM算法的估计效率问题,发现当删失比较大时,EM算法存在过度迭代现象,使得估计结果偏离数据来源的分布,为此提出了结合加权绝对偏差信息准则进行参数估计的方法,仿真算例说明了文中所提方法的有效性。 [1]TONG Ng H K,WANG Z. Statistical estimation for the parameters of Weibull distribution based on progressively type-I interval censored sample[J]. Journal of Statistical Computation and Simulation, 2009, 79(2): 145-159. [2]苏锦霞, 张艺赢, 田丽娜. Ⅰ型逐阶区间删失Weibull数据的统计分析[J]. 兰州大学学报: 自然科学版, 2011, 47(5): 109-114, 119. [3]MOKHTARI E B, RAD A H, YOUSEFZADEH F. Inference for Weibull distribution based on progressively type-II hybrid censored data[J]. Journal of Statistical Planning and Inference, 2011, 141(8): 2824-2838. [4]JOARDER A, KRISHNA H, KUNDUC D. Inferences on Weibull parameters with conventional type-I censoring[J]. Computational Statistics and Data Analysis, 2011, 55(1): 1-11. [5]GHITANY M E, TUAN V K, BALAKRISHNANC N. Likelihood estimation for a general class of inverse exponentiated distributions based on complete and progressively censored data[J]. Journal of Statistical Computation and Simulation, 2014, 84(1): 96-106. [6]郑明, 杨艺, 郑宇. 基于分组数据的Weibull分布的参数估计[J]. 高校应用数学学报A辑:中文版, 2003, 18(3): 303-310. [7]吴耀国, 周杰, 王柱, 等. 随机删失数据下基于EM算法的Weibull分布参数估计[J].四川大学学报: 自然科学版, 2005, 42(5): 910-913. [8]任瑞, 周秀轻. 逐步Ⅰ型区间删失数据下的参数估计[J]. 南京师大学报: 自然科学版, 2011, 34(3): 7-12. [9]张颂, 王德辉. 熵损失下定数Progressive删失情形Weibull分布尺度参数的估计[J]. 吉林大学学报: 理学版, 2012, 50(2): 219-226. [10]LIN C T, CHOU C C, HUANG Y L. Inference for the Weibull distribution with progressive hybrid censoring[J]. Computational Statistics and Data Analysis, 2012, 56(3): 451-467. [11]PARK B J, LORD D. Application of finite mixture models for vehicle crash data analysis[J]. Accident Analysis and Prevention, 2009, 41(4): 683-691. [12]蒋卉, 汤银才. 混合Weibull分布参数估计的ECM算法[J]. 系统科学与数学, 2010, 30(1): 79-88. [13]木拉提·吐尔德, 胡锡健. EM算法在删失数据分布和混合分布参数估计中的应用[J]. 统计与决策, 2011, 339(15): 161-164. [14]张晓勤, 王煜, 卢殿军. 混合指数威布尔分布的参数估计[J]. 河南大学学报: 自然科学版, 2012, 42(3): 230-233. [15]田玉柱, 田茂再, 陈平. 数据分组和右删失下混合广义指数分布的参数估计[J]. 应用概率统计, 2012, 28(6): 561-571. [16]MC LACHLAN G, PEEL D. Finite mixture models[M]. USA,New York: John Wiley & Sons, Inc, 2000. (编辑王冬) Parameters estimation of generalized progressive type-I interval-censored mixture Weibull-distributed data YUANYanhua (School of Sciences, Heilongjiang University of Science & Technology, Harbin 150022, China) This paper is a response to the previously insufficient study of the method designed for the parameter estimation for the generalized progressive type-I interval-censored data based on the finite mixture. The study building on finite mixture Weibull-distribution model looks at the effectiveness of Expectation-Maximization(EM) algorithm used for the parameter estimation for generalized progressive type-I interval-censored data and produces a modified EM algorithm. The modification starts with giving the EM algorithm used for the parameter estimation, followed the simulation examples to explain the excessive iteration produced by EM algorithm when used for the parameter estimation for the generalized progressive type-I interval-censored data, and culminates in the necessity for stopping weighted absolute deviance information criterion involved in EM algorithm. The modified EM algorithm is free from the drawback inherent in EM algorithm incapable of determining the time right for stopping iteration when used to perform parameter estimation, thus allowing for a quick production of satisfactory estimators, following an appropriate selection of the initial value. The simulation verifies the viability of the algorithm. generalized progressive type-I interval censoring; weighted absolute deviation information; finite mixture Weibull distribution; EM algorithm 2013-12-11; 2014-03-25 苑延华(1969-),女,辽宁省本溪人,教授,博士研究生,研究方向:概率统计、运筹学与控制论,E-mail:yuanhua-69@sina.com。 10.3969/j.issn.2095-7262.2014.03.021 O213 2095-7262(2014)03-0323-09 A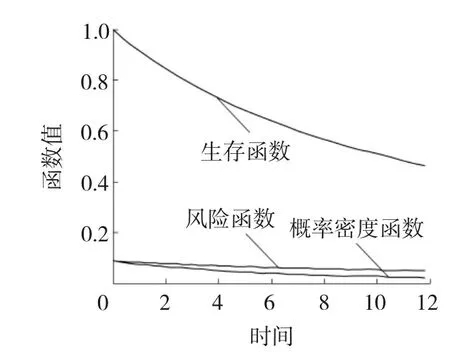

4 基于加权绝对偏差信息准则的EM算法
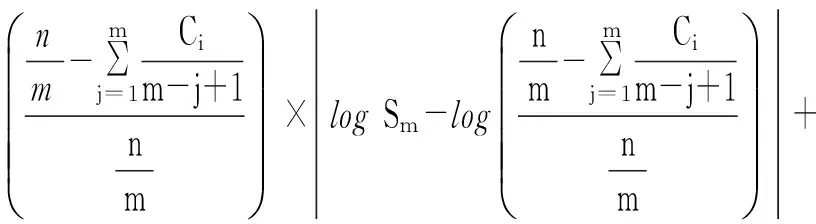




5 结束语
