基于模糊理论的汽轮机故障诊断∗

吕占杰，唐贵基，韩国栋，吴章勤，王 进，万书亭

(1.华北电力大学 机械工程系，河北 保定 071003；2.华北电力大学 云南电网公司研究生工作站，云南 昆明 650217；3.云南电力试验研究院（集团）有限公司 电力研究院，云南昆明 650217)

0 前言

汽轮发电机组是火电厂的核心设备，是一种连接高速旋转的大型精密设备.由于其设备结构的复杂性和运行环境的特殊性，汽轮发电机组的故障率不低，而且故障危害性很大.因此，汽轮发电机组的故障诊断一直是设备诊断研究的焦点[1,2].

旋转机械的故障多种多样，已知的故障种类有二三十种，常见的故障有：不平衡、不对中、动静件摩擦、机械零件松动、转子弯曲、油膜涡动、油膜振荡等.一般的汽轮机故障是某几种故障的综合，并不是某单一故障[3,4].

所谓的故障诊断是指校核可测变量或不可测的估计变量是否在正常的运行范围内[5].故障机理是故障的内在本质和产生原因.目前，对汽轮机故障机理的研究主要从故障规律、故障征兆和故障模型等方面进行.一种故障可能引起多种征兆，而一种征兆又往往对应数种故障.每个转子都有程度不同的不平衡，不对中等故障.因而，转子的故障诊断不是经典集合论中的两值逻辑判断问题；而是讨论在转子所具有的几种故障中，相对隶属于哪种故障、其程度又如何的问题.因此应用模糊集合论的方法来处理故障诊断问题是比较恰当的[6].

1 模糊诊断原理

故障模糊诊断的基本原理是利用模糊变换的原理、最大隶属度和阈值原则，根据各故障的原因与征兆之间不同程度的因果关系，在综合考虑所有征兆基础上来诊断旋转机械振动故障的可能原因.

在模糊数学中，把既属于A又不属于A的元素划在0与1之间，对这一特性用隶属函数来描述，设隶属函数为µA(x)，则µA(x)∈[0，1]，模糊子集A可由隶属函数µA(x)来描述.当隶属函数中的变量取具体值时，如x=xi，则称uA(xi)为xi对模糊子集A的隶属度[7].模糊故障诊断方法就是根据某些症状的隶属度来求出各种故障的隶属度，从而表征各种故障存在的倾向性，为判断机组的故障和采取维护措施决策时提供科学依据.对汽轮发电机组转子来说，由于影响其振动的原因很多，故应对每个对象根据模糊综合评判指标的大小分析出主次.因此采用模糊综合评判法.模糊综合评判首先是对各个因素进行单独评判，然后再对所有因素进行综合评判[8].

两个集合，U为故障原因，V为症状集.例如在转子故障诊断中：U=(u1,u2,···,um)(不平衡，不对中，轴弯曲，···)；V=(v1,v2,···,vn)(一倍频峰值，二倍频峰值，N倍频峰值，···).由于各种故障原因和征兆表现之间是一种模糊关系，因此对于某类相同设备通过实验、理论分析或经验方法确定U，V之间的模糊关系矩阵如下

其中rij=R(uivj)为糊关系R的隶属度.根据监测数据而获得的各种征兆而构成一组特征向量X：X=[x1,x2,···xn]T；其中xj=µx(vj)，表示xj对vj的隶属度(j=1,2,···m)，则X、Y和R之间满足模糊变换关系

这就是模糊综合评判，由此可以导Y=[y1,y2,···,ym]T，根据隶属度yi=µy(ui)(i=1,2,···m)的大小顺序可以构成下述序列

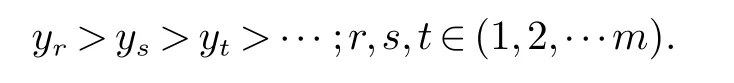
这就提供了待检信号的特征归结为某种故障原因可能性的顺序，为诊断决策提供了依据[9].

根据前述，首先要确定征兆子集的隶属度函数.在汽轮发电机组转子振动的故障诊断中，对于“振动大”与“故障严重”这一模糊关系，经验证明，振动较小时故障不明显，而这种平时振动较小的机组，当振动达到一定程度后，故障就明显发生.通过参考以往大量汽轮机故障诊断实例，取升半柯西分布型隶属函数较为合适，其数学表达式为

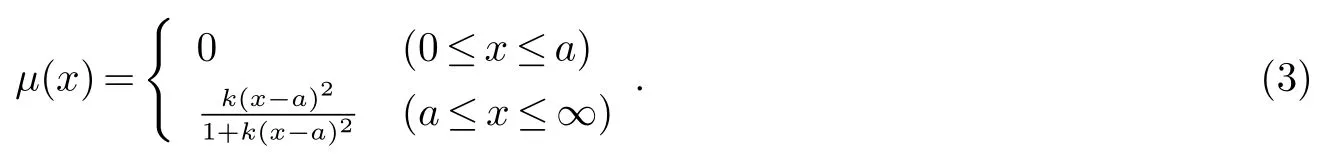
在所研究的问题中，取系数a=0，即x为正域均有效，上式可简化为

根据多次试验的研究经验，k值取为频谱分量数值均值平方的倒数最为恰当，即

式中n为xi=0的个数.

另外，对频谱分析中各谐波的幅值，采用不同的隶属函数，对于一阶基波，取式(1)中的µ(x)作为衡量“振动大”的度量，对于油膜振荡出现的半波幅值，取作为衡量“振动大”的度量，而其它各种倍频则可取作为“振动大”的度量[10].

2 模糊诊断实例

由于大部分轴系故障都在振动信号上反应出来，因此，对轴系故障的研究总是以振动信号分析为主[7].根据现场采集到的仿真信号，首先利用Matlab编程把输入的仿真信号按照表1进行分频.然后按照公式（3）求出征兆隶属度，再利用向量乘积（2）求出各故障的隶属度大小.

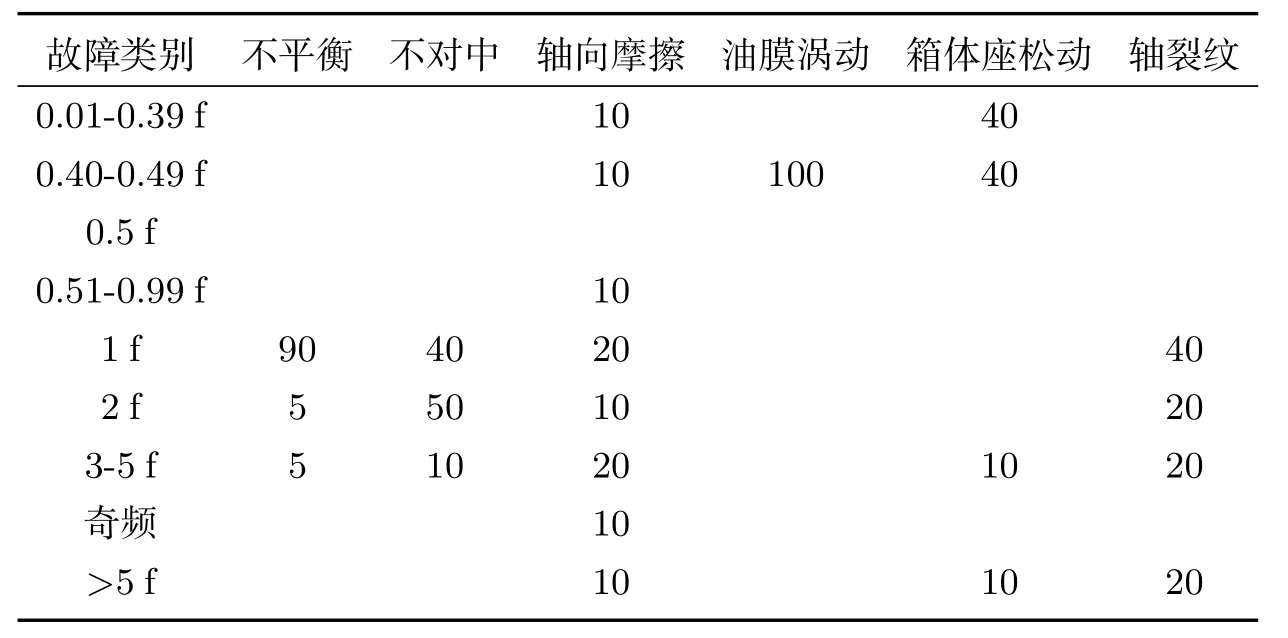
表1 汽轮发电机组转子机械故障的故障模型[11]

从表1中可以分析出：转子不平衡的频谱特征是1倍频占的比重最大，其他各倍频均可忽略.转子不对中的频谱特征是1倍频与2倍频所占的比重最大，其他的倍频可以忽略.轴向碰摩的频谱特征是低频段中各倍频所占的比重相当.油膜涡动的频谱特征是0.4-0.49倍频占所有的比重.箱体松动的频谱特征是0.01-0.39倍频和0.40-0.49倍频占很大的比重.轴裂纹的频谱特征是1倍频，2倍频，3-5倍频，高倍频分别占较大比重且1倍频的比重最大，其他倍频可以忽略.

2.1 实例分析1

根据故障信号的特征，例如输入的仿真信号是

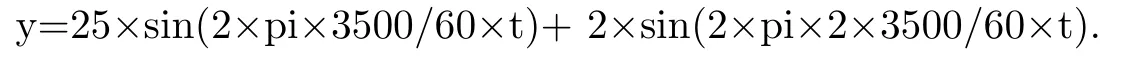
运行结果如下

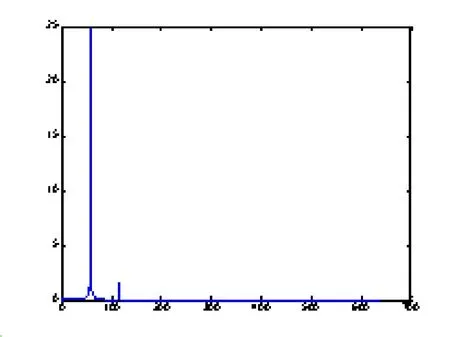
图1 故障信号频域图

运行的各频段数据调入诊断主程序后，可得到结果如表2所示.

表2 故障的各隶属度

因为不平衡故障的隶属度最大，因此信号反应出转子最可能的故障是不平衡.

2.2 实例分析2

由于故障的模糊性以及不确定性，有时分析结果会出现几个故障的隶属度数值较大且较接近的故障，这就需要一种判别方式来判定故障的准确性.

模糊综合评判是考虑两个论域，即故障论域和征兆论域，利用故障征兆的隶属度和诊断权矩阵，求解各种故障的隶属度.

若设备的故障论域Y={y1,y2,···ym}，其中各元素yi的隶属度µBi(yi)组成模糊向量B=[µB1(y1),µB2(y2),···µBm(ym)]T.

征兆论域X={x1,x2,···xm}，其中各元素xj的隶属度µAj(yj)组成征兆模糊向量A=[µA1(x1),µA2(x2),···µAm(xm)]T.

故障的识别是把测量到的征兆向量A，归入到标准故障模式类M1,M2,···Mn中一个与它相似的模式中.常用贴近度或最小距离法.待识别的样本被归入贴近度最大或距离最小的一类中，距离计算公式有闵可夫斯基(Minkowski)距离，海明距离(Hamming)，欧几里德(Euclid)距离等[12].

Minkowski距离为

P=1时，d(A,B)为Hamnfing 距离；p=2时，d2(A,B)为Euclid距离.

最小距离的识别原则是对论域U上的n个标准模式，使取最小值，则A与Mi的距离最小，A应归入模式Mi中.利用此方法时，征兆向量的构成不同于上面的隶属度计算，而是用待识别振动信号各频率段幅值所占总能量的百分比构成，与形成标准故障模式类的征兆在同一个征兆空间，计算在征兆空间中的距离.距离的大小表示两者在空间靠近的程度，不反映故障的大小[13].

例如，某电厂某汽轮机轴承发生超常振动时，利用信号采集传感器得到1倍频振幅x1=76µm；2倍频振幅x2=39µm；3倍频振幅x3=50µm.

表3 隶属度较大的几种故障

在频谱分析中有三种主要频率成分1倍频、2倍频和3倍频，各成分所占总能量的百分比构成频谱征兆向量A=[0,0,0,0,0.46,0.24,0.30,0]T，计算待识别向量A与标准故障模式不平衡，轴承对轴径偏心，轴线不对中频谱征兆向量的Euclid距离如表4.

表4 Euclid距离

显然征兆向量A表示的模式与不对中故障的标准频谱模式最接近，而与不平衡故障的标准模式相距最远.从而可以得出的结论是，机组最可能发生的是不对中故障，故障的隶属度是0.672.

3 结论

本文给出了汽轮机故障的一种综合模糊诊断方法.首先针对汽轮机组常见的六种故障，根据提取的故障信号分频段进行数据分析，得到各故障的隶属度.由于某些较大故障隶属度较接近，通过Minkowski距离公式计算隶属度距离大小.从而更准确地得出汽轮机组的故障.此模糊诊断方法已经在工业控制领域，家用电器自动化领域和其他很多行业中解决了传统控制方法无法或者难以解决的问题，对汽轮机组的故障诊断有重要意义.另外，模糊诊断中也存在问题，尚缺乏重大的突破：

（1）如何获得模糊规则及隶属函数即系统设计方法，目前完全凭经验来进行；

（2）如何保证模糊系统的稳定性即如何解决模糊控制中关于稳定性和鲁棒性的问题.