长时间序列遥感数据回归分析支持下的植被变化分析∗

阿斯姆古丽·阿纳耶提，师庆东，刘 曼，唐存士，王安隆

(新疆维吾尔自治区绿洲生态重点实验室，新疆大学 资源与环境科学学院，干旱生态环境研究所，新疆 乌鲁木齐 830046)

0 引言

遥感动态监测土地利用、土地覆盖和植被变化的具体方法多样，图像差值法是目前使用最多的土壤动态探测方法.这种方法多使用间断的、非连续的遥感数据，计算结果容易受到偶然因素的影响.当有一组长期的连续随时间变化的数据时，以上的方法也不便于充分利用序列数据.对于连续随时间而产生遥感数据，经几何校正后在各幅图中同一个确定位置的像元点上，都将产生一组随时间变化的点数据序列，这一组数据实际上反映出该点的植被变化过程，描述出这些点的变化过程以及通过变化过程预测今后的发展趋势以及区域的发展趋势，具有重要的现实意义.由于地理环境的区域分异规律和各种自然、人文因素的影响，不同的地区表现出不同的变化特征，对于一个遥感时间序列情况的复杂度使得无法对每一个像元建立精确的模型，一般情况下一幅遥感数据将包含成千上万个像素点，对于这些点的时间变化序列可能包含多种变化模式，若想将每一个像元的时间序列进行准确分析在目前情况下是困难的和不经济的.但是，退而求其次，若能从时序中发现内在的演化宏观区域趋势，能够判断出它在未来某一时刻的大致范围也有很重要的价值.

因此需要一种相对简化的模型进行分析，模型的简明便于人们的理解，如果模式的结构越复杂，它就越难于被解释，而简明的数学表达形式对进行数学分析与解释处理也比较方便.

当回归分析中的自变量是时间单位时，许多经典的回归理论都能用于时间序列的自回归模型中[1∼6]，对此曼和沃尔德在1943年已经作了证明，而线性函数也被认为是逼近真实现象、数学表达简明的时间序列分析工具[7].

出于以上考虑，本文用年时间单位作为自变量，将每个像元的FVC值作为因变量，在GIS的支持下，利用线性回归理论来分析和预测中国西部干旱区植被变化.

1 研究区范围

研究区北部界限从阿尔泰山脉，沿中蒙边界至阴山西端，南部以昆仑山山脉为界，西起中国与中亚各国的边界，东部则以贺兰山为界（参见图1）.

图1 研究区位置示意图

图2 中国西部干旱区1982∼2000年FVC指数斜率分布

2 数据与数据处理

本次研究所使用的数据为FVC，由美国亚利桑那州立大学曾旭斌博士提供，该数据采用MVC方法提取[8].数据空间分辨率8 km，时间为1982∼2000年每年FVC指数图像，共19幅.

对8 km分辨率图像分别做了几何纠正，由于采用了统一的投影方式.通过ARCGIS将FVC影像转为栅格(grid)文件并进行工作区切割，本次研究的绝大部分工作是在ARCGIS8.3软件的支持下完成.

3 计算公式及计算结果

3.1 回归分析原理

线性回归分析是处理具有线性相关的两个变量x与y之间关系的工具.首先要通过实验得到这两个变量的若干组数据，然后建立他们的线性关系式.最后对其进行显著性检验.

通过最小二乘法原理可以求得反映随时间变化趋势的斜率

通过对每一个像元点方程的拟合，计算出了每个点的斜率，斜率也反映了该点变化趋势，斜率为正，表示该点的植被改善，斜率为负，表明该点的植被退化，图2就是根据式(1)在ARCGIS中的AML语言支持下计算的1982∼2000年植被斜率分布图.

3.2 回归方程的方差检验及意义

回归是否显著，必须经过显著性的检验，也就是说并不是所有的点都是可以满足线性要求的，每一个点都要接受显著性检验.对于线性回归，可以使用相关系数法和方差分析方法进行显著性检验，本次研究使用方差分析检验法.

已知

可以将因变量y的总离差平方和分解为两部分，令

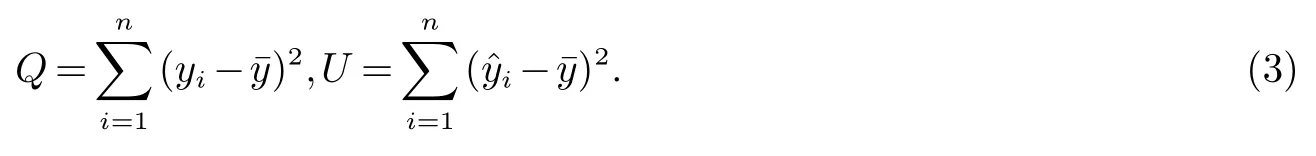
称Q为残差（剩余）平方和，称U为回归平方和，Q反映了随机误差，是观测值与回归值距离的平方和，Q值越小说明观测值与回归直线的距离越近，回归效果越好，否则，则相反.

在假设H0，β1=0成立的条件下，统计量

服从第一自由度为1，第二自由度为n-2的F分布.在给定显著水平α，可按方差分析的检验方法进行检验.当F>Fa(1,n−2)时，否定原假设，说明回归方程是显著的，即说明x与y有线性关系，则判定所建立的回归方程是有意义的，当F≤Fa(1,n−2)时，接受原假设，说明回归方程不显著，即说明x与y无线性关系，则判定所建立的回归方程无意义.

图3是根据1982∼2000年数据所建的回归方程的F检验（深色为符合点、浅色为不符合点）.其中第一自由度为1，第二自由度为17（19-1-1），显著水平α=0.05，从图3可以看出，准噶尔盆地中心、天山北坡绿州带、塔里木河流域、叶尔羌河流域、喀什地区、和田地区、阿尔金山和祁连山北坡、阿拉善-柴达木盆地东侧的地区整体区域上符合F检验，这些地区的变化与时间有很强的回归关系，且这些点的分布与图2有相近的分布.

3.3 斜率为零的假设检验与植被稳定区

从图3中可以看出，1982∼2000年这一段时间内，与时间变化有回归关系的区域并不广泛，也就是说，在这近20年的变化中，有一部分是与时间有相关性的，而另一部分是无法通过显著性检验的.对无法通过显著性检验的数据大体上可分为三种情况：一种是与时间序列变化有关系的植被变化，这种变化有正有负，主要根据斜率的正负决定，并可通过F检验；一种是植被稳定区，其斜率基本为0；最后一种是植被剧烈波动区，其残差太大，难以与时间变化做回归分析.因此，在进行了回归分析的F显著性检验后，有必要对不符合F检验的地区进行斜率为0的样本假设检验，符合假设的地区为植被稳定区.既不符合F检验又不符合斜率为0的假设检验的为植被非线性回归波动区.

对小样本总体平均值的统计假设可用t分布来检验，该统计量计算式为

采用此方法笔者利用每个像元点的19个序列值采用式(5)计算，得到计算结果分布图，又通过t分布数值表查得当自由度为18，置信度α=0.05的临界值为2.10，对计算结果分布图按2.101分类，小于2.101的区域为符合t假设检验的区域，为植被稳定区，否则为不稳定区.计算结果见图4.

图3 根据1982∼2000年数据所建的回归方程的F检验（深色为符合点，浅色为不符合点）

图4 根据1982∼2000年数据所建的回归方程的斜率为0的t检验的分布（深色为符合点，浅色为不符合点）

3.4 结果讨论

1.通过对差值分析和回归分析进行比较后认为，将具有时间序列的植被指数信息对时间进行回归分析后，所得到的结果比简单的差值分析的结果稳定，而且回归方程充分利用了所有的图像信息，并且具有延伸预测的理论基础.

2.通过对回归方程的F检验和t检验结果（图3和图4）可以看出所得到的回归方程，不服从F分布的地区基本上服从t分布.因此，可以使用F分布或t分布来分析植被的变化区和稳定区.笔者还对既不服从F分布又不服从t分布的区域作了分析，不服从这二者分布的区域有2 765个像元，占总像元数39 554的0.069 7，也就是说93%以上的单元或者服从t分布，或者服从F分布.因此对于中国西部干旱区的植被变化基本上可以分为两种情况，植被基本稳定区和植被稳定变化区，而植被变化区可以通过斜率法、图像差值法、相关系数法等方法分为正向变化区和负向变化区.