非均衡投资收益极大指派问题
2014-11-01王立柱
王立柱,刘 阳,石 洋,孙 军
(1.沈阳师范大学 数学与系统科学学院,沈阳 110034;2.中国人民解放军93115部队,沈阳 110034)
0 引 言
非均衡投资收益极大的指派问题是指有m个公司要参与n个项目的投资,由于每个公司业务能力不同、项目的不同,各公司投资各个项目的收益也不同,现希望从m个公司中选出k(0<k≤gmin{m,n})个公司去投资n个项目中的k项,每个公司只投资一个项目,每个项目只由一个公司完成,使得总收益最大。此类问题可以看作为投资小于公司和项目数的非标准极大指派问题,记为极大(m,n,k)问题。当m=n=k时即为标准极大指派问题。
对于极大(m,n,k)问题,文献[1]指出标准极大指派问题可以转化为标准指派问题(极小指派问题),利用经典的匈牙利法求解。另外,文献[2]提出了非方阵极大极小指派问题且文献[3]给出了贪婪算法;文献[4]中提出了C指派问题;文献[5]任务数多于人数的指派间题;文献[6]中提出了多目标指派问题及其在物资供应中的应用。查阅大量相关文献[7-11],没有对上述问题给予好的解法。本文将给出解决此类问题的相关理论及重要结论,并给出解决问题的增反点算法。
1 非均衡投资收益极大指派问题描述和数学模型
假设有n个公司且有n个投资项目,每公司投资不同项目的收益不同。现要从n个公司中选出k(0<k≤n)个投资n个项目中的k项,求选哪k个公司投资哪k个项目才能使总收益最大。即极大(n,n,k)问题。
更一般的情形,从m个公司中选出k(0<k≤min{m,n})个公司去投资n个项目中的k个项目使得总投资收益最大,即极大(m,n,k)问题。极大(n,n,k)与极大(m,n,k)问题统称为非均衡投资收益极大指派问题。
其中极大(m,n,k)问题的数学模型为
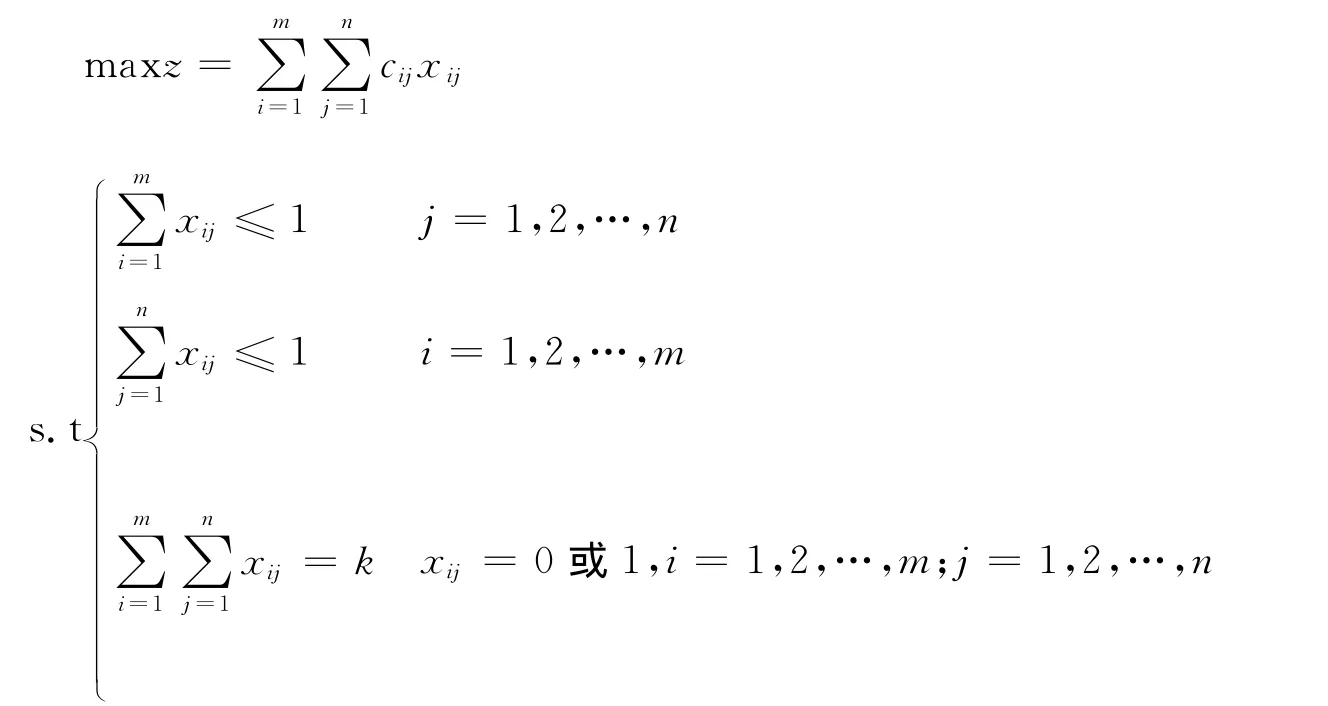
(cij)m×n>0称为问题的系数矩阵,当取m=n时,得极大(n,n,k)问题的数学模型。当取m=n=k时,即是标准极大指派问题的数学模型。
该问题实质是求解m×n阶系数矩阵中位于不同行、不同列的k(0<k≤min {m,n})个元素求和最大。当k较小时,问题处理较为简单;通常对k较大时进行研究。
2 反点及相关结果
定义1 在阶数为n的方阵中,若某元素所在的行和列的其他元素都是方阵中的最大元素M,则此点称做反点。如式(1)中r11就是反点,其中·表示n阶方阵中的任意元素。

定理1 对于n阶标准极大指派问题,反点一定不含于最优解中。
证明 以(n=7)为例,设式(2)为标准极大指派问题的系数矩阵。假设w1={r14,r23,r32,r41,r55,r66,r77}是标准极大指派问题的最优解,且包含反点r14,记相加之和v1=r14+r23+r32+r41+r55+r66+r77。

从属于最优解并且不是反点的元素中任取一元素如r55,现选取r15和r54分别替换r14与r55得到新的可行解w2={r15,r23,r32,r41,r54,r66,r77},如(3)所示。记相加之和v2=r15+r23+r32+r41+r54+r66+r77。

由于r15=M、r54=M,显然v1≤v2,这与w1是最优解矛盾。对于n阶系数矩阵结论同样成立,因而结论得证。
定理2 对于n阶标准极大指派问题,如果系数矩阵中有k个反点,则最优解中一定有2k个最优点处于此k个反点所在的行与列,剩下的n-2k个最优点一定是由去掉反点所在行、列所得到的n-k阶方阵中不同行、列的n-2k个和达到最大的元素组成。
证明 由上面的结论知,反点必不是n阶极大指派问题最优解w1中的元素。因为最优解须满足处于不同的行与列,因而,最优解中必有一个元素处于反点所在的行与列上。所以,最优解w1中必有2k个点处于反点所在的行与列。
去掉这k个反点所在的行与列的元素,得到n-k阶方阵。由于n阶标准极大指派问题的最优解w1中含有n个位于不同行、列的元素,其中2k个处于反点所在的行列,剩余n-2k个最优点必落在未被去掉的n-k阶矩阵中,且位于不同行、列和最大的n-2k个点。倘若剩余的n-2k个最优点不是n-k阶方阵中位于不同行、列和最大的n-2k个点,则与w1是最优解矛盾。定理得证。
由定理2可知:对于n阶标准极大指派问题,若系数矩阵含有k个反点,则问题最优解就转化为求划去反点所在行、列得到的n-k阶方阵中位于不同行不同列的n-2k个和最大的点。反之,若求n-k阶方阵中位于不同行不同列的n-2k个和最大的点,可以通过增加k个反点转化为求n阶标准极大指派问题。
定理3 对于求解极大(n,n,k)问题,可通过增加n-k个反点求解2n-k阶标准极大指派问题得到。
证明 当k=n时,即为n阶标准极大指派问题,当k<n时,即求n阶系数矩阵中位于不同行、列且和最大的k个点的位置,不妨在该n阶矩阵的外面增加n-k个反点,此时变成一个2n-k阶矩阵,由定理1、2求解此2n-k阶标准极大指派问题,便可得到极大(n,n,k)问题的最优解。
定理4 对于求解极大(m,n,k)问题,可通过先将其系数矩阵补成max{m,n}阶方阵,增加max{m,n}-k个反点求解2max{m,n}-k阶标准极大指派问题得到。
证明 将极大(m,n,k)问题的m×n阶系数矩阵(rij)m×n增加行或列的0元素得到max{m,n}阶方阵,由定理3知,增加 max{m,n}-k个反点后 max{m,n}阶方阵变成2max{m,n}-k阶方阵,以此方阵为系数的指派问题的最优解中除处于反点上的2(max{m,n}-k)个最优点外,其余的最优点组成极大(m,n,k)指派问题的最优解。以m=3,n=4,k=3为例,如(4)所示。先将3×4阶系数矩阵增加一行0元素,然后增加一个反点,根据上面的结论知,极大(3,4,3)指派问题的最优解可通过求解5阶标准极大指派问题得到。

3 提出的算法
求解极大(n,n,k)和(m,n,k)问题的算法如下:
第1步 标准化极大派问题的系数矩阵。
1)若求解极大(n,n,k)问题,则系数矩阵不变。
2)若求解极大(m,n,k)问题,则增加行或列的0元素,将系数矩阵变为max{m,n}阶方阵。
第2步 计算所需增加反点数。
经标准化处理后,得到的依然是n阶方阵,在此方阵的外侧增加n-k个反点使之变换成2n-k阶方阵;极大(m,n,k)问题系数矩阵变为 max{m,n}阶方阵,在此方阵的外侧再增加 max{m,n}-k个反点使其变成2max{m,n}-k阶方阵。
第3步 求解经第2步处理得到的方阵为系数矩阵的标准极大指派问题。
利用匈牙利法[12]或已有的求解标准指派问题的算法求解[13-16]。
第4步 计算最优解。
通过以上3个步骤,可以得到标准指派问题的最优解,然后将此最优解划去位于反点所在行和列的最优点,剩余的最优点即为非均衡极大(n,n,k)及(m,n,k)指派问题的最优解。
4 Matlab程序及实例
算法的Matlab程序代码如下:

例1 设有5个公司和4个投资项目,每个公司投资各个项目的收益如表1,现希望从这5个公司中选出3个投资4个项目中的3项,问选哪3个公司投资哪3个项目才能使总收益最大。
解 此问题是极大(m=5,n=4,k=3)问题,其的系数矩阵是5×4阶矩阵,且=73.6,解决此问题可以补一列0元素且增加2个反点,将系数矩阵处理为R1=(rij)9×9。以R1为系数矩阵解标准极大指派问题,可得对应极大(m=5,n=4,k=3)问题的最优解矩阵R*。
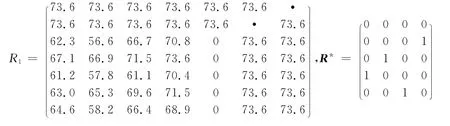
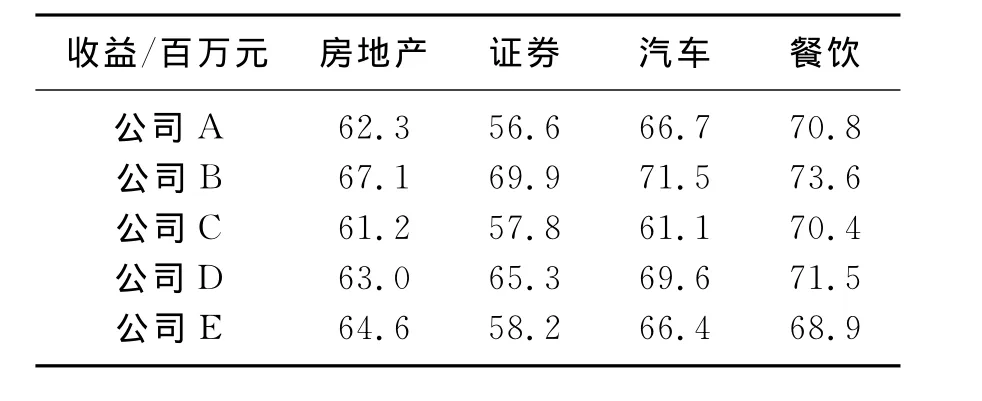
表1 投资项目表
运行实例:

5 结 语
本文对极大非均衡投资问题给出了反点算法,此方法通过增加反点使问题变得简单化、易于处理。此算法同时也应用于具体实例,实验结果表明了该方法的科学性和有效性。同时也为解决指派问题提供了新思路、新方法。
[1]钱颂迪.运筹学[M].北京:清华大学出版社,1990:123-204.
[2]PAUL C,JE B.A genetic algorithm for the generalized assignment problem[J].Comput Opera Res,1997,24(1):17-23.
[3]SHARKEY T C.Greedy approaches for a class of nonlinear Generalized Assignment Problems[J].Disc Appl Math,2010,158(1):559-572.
[4]白国仲,毛经中.C指派问题[J].系统工程理论与实践,2003,23(3):107-111.
[5]张新辉.任务数多于人数的指派问题[J].运筹与管理,1997,6(3):20-25.
[6]宋业新,陈绵云,张暑红.多目标指派问题及其在军械物资供应中的应用[J].系统工程理论与实践,2001,21(11):141-144.
[7]殷人昆,吴阳,张晶炜.蚁群算法解决指派问题的研究和应用[J].计算机工程与应用,2008,30(4):43-46.
[8]刘树立,于丽英.人数与任务数不相等的指派问题[J].运筹与管理,2005,14(2):64-66.
[9]吴艳群,董鹏.求解大规模不对称指派问题的通用模拟退火算法[J].兰州交通大学学报,2008,27(4):149-153.
[10]胡劲松.模糊指派问题求解方法研究[J].系统工程理论与实践,2001,4(9):94-99.
[11]秦学志,王雪华.一类最优指派问题的动态规划模型[J].数学的实践与认识,1996,26(3):212-216.
[12]熊燕华.对国内求解指派问题的匈牙利法改进的评述[J].中国制造信息化,2009,63(04):63-67.
[13]孙晓雅.一种新的离散粒子群算法在指派问题中的应用[J].计算机应用研究,2009,26(11):201-206.
[14]贺学海.单纯形法解决LP问题的研究[J].沈阳师范大学学报:自然科学版,2010,28(1):45-49.
[15]夏少刚,费威.基于最小调整法求解最短时限指派问题[J].数学的实践与认识,2009,39(17):140-149.
[16]李岩,郭强.非确定型指派问题的求解算法[J].计算机工程与应用,2009,45(15):61-65.
