基于RBF神经网络的电喷天然气发动机空燃比控制
2014-10-31任金霞何富江曹威锋
任金霞 何富江 曹威锋
(江西理工大学电气工程与自动化学院 江西赣州 341000)
引言
天然气作为发动机的理想燃料,在经济性和排放性方面都优于汽油,电喷天然气发动机的动力性与空燃比紧密相关。此外电喷天然气发动机的三元催化转化器的转化效率和空燃比密切联系,其经济性、排放性受空燃比的影响非常大。因此,对空燃比的精确控制[1]对发动机性能提高有着积极的影响。
目前空燃比的精确控制是国内外的研究热点,用于控制的方法也有很多,如基于模型的控制方法、自适应控制算法、模糊算法等。本文采用RBF神经网络和常规PID控制算法相结合的空燃比控制方法,针对天然气发动机的延迟,采用RBF神经网络对空燃比进行预测[2,3],而后将预测的空燃比信号传递给PID控制器控制燃气量,从而实现空燃比的实时闭环控制。并利用Matlab/Simulink软件建立RBF神经网络电喷天然气发动机的仿真模型[4],在工况突变的各个情况下进行仿真实验。
1 影响电喷天然气发动机产生延迟的因素
电喷天然气发动机空燃比控制就是控制缸内混合气浓度,目前的空燃比传感器只能安装在排气管内而不是直接监测混合气浓度,因此会造成空燃比控制系统的延迟。其延时包括混合气形成过程的传播延迟、混合气体点燃的着火延迟、燃烧完成后废气到氧传感器的传播延迟、传感器的响应延迟。
混合气体形成过程的传播延迟与发动机的转速、进气门及排气门的开度有关。
由于天然气分子结构和物理特性比较稳定,因此有着火慢的特点,我们记其着火延迟时间为。
燃烧完成后废气到氧传感器的传播延迟t3与排气管容积、排气管结构、氧传感器位置、排气温度、排气压力等有关。
空燃比传感器的响应延迟t4与发动机的工况参数、发动机的结构以及传感器特性有关。
2 前馈PID控制
发动机的空燃比受多种因素的影响,如节气门开度、转速、负载、燃料喷射精度、响应时间等,PID闭环控制能根据反馈实时调整喷气量,达到精确控制喷气量的目的。
图1为电控喷射天然气发动机PID控制框图,由图可知该系统分为前馈控制和PID闭环反馈两个部分。
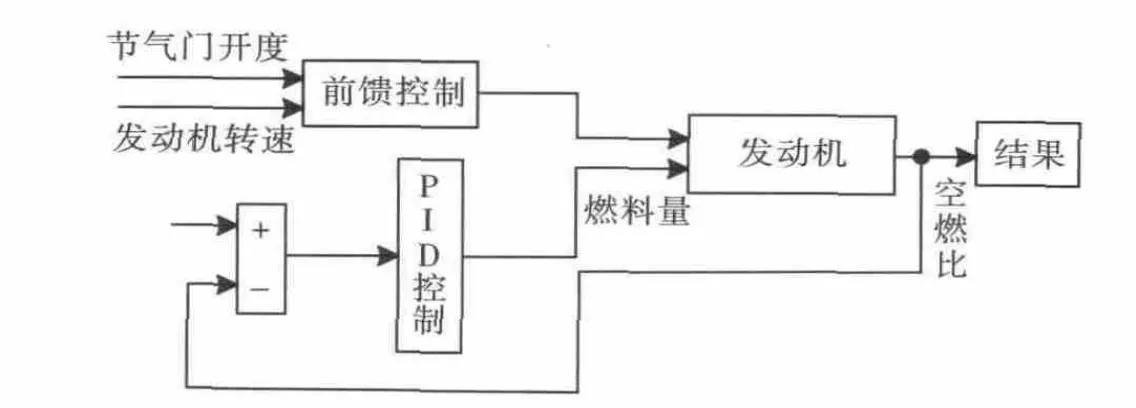
图1 前馈PID的空燃比控制模型
前馈部分根据当前的转速和节气门开度决定基本的燃料喷射量,闭环反馈部分在确定了PID参数后,通过反馈得到的空燃比不断与设定的理想空燃比16.7进行比较,偏差进入PID控制器,根据偏差调节喷气量,不断重复使电喷天然气发动机空燃比不断逼近理想空燃比。
3 无延迟的空燃比控制
由于电喷天然气发动机是一个有延时的系统,对空燃比精确控制造成困难,尤其在过渡工况下,转速及节气门开度剧烈变化,传输延迟甚至会造成控制失调。因此本文采用了RBF神经网络对空燃比进行无延迟预测。
3.1 无延迟控制模型
针对电喷天然气发动机空燃比传输延迟分析可知,采用RBF神经网络实现空燃比的预测,并经过延时后与发动机空燃比信号比较并调节神经网络。当误差被控制在所设定的范围之内时,神经网络的输出信号即为无传输延迟的空燃比信号。用这个信号作为PID控制器的反馈信号,由PID控制器控制燃料的喷射量,即可实现对空燃比的实时控制。无延迟的空燃比控制模型如下图所示。

图2 无延迟的空燃比控制模型
3.2 RBF神经网络模型
RBF神经网络是一种三层神经网络,具有学习速度快,非线性逼近能力强、避免局部最优等特点。
在训练之前,首先要确定RBF网络的结构,在本文中所采用的RBF网络采用三输入单输出结构,隐含层转换函数采用高斯函数,通过多次训练确定隐含层最佳神经元个数为9个。输入向量为
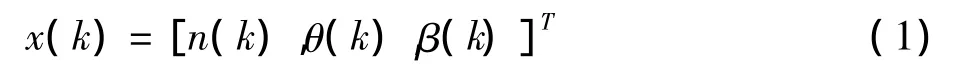
式中n(k)表示 时发动机转速;θ(k)表示k时节气门开度;β(k)表示k时空燃比。
RBF的输出y(k)为k时刻网络输出层神经元的期望输出,在本文中来自空燃比传感器的输出信号。由于预测的是无传输延迟的空燃比信号,x(k)、y(k)均为按时序输入输出数据。将常规PID控制模型的空燃比传感器输出的反馈信号改为由神经网络输出的信号即可调整为基于无传输延迟的空燃比控制模型,如图3所示,空燃比传感器的输出信号用于监督神经网络训练结果以达到在线预测无传输延迟的空燃比信号的目的。
RBF网络结构如图4所示。

图3 RBF神经网络模型子图
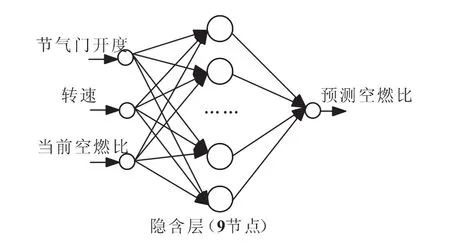
图4 RBF网络结构
4 实验仿真分析
在天然气发动机运行时经常出现的是瞬态工况,即发动机的转速和负荷不断地变化。瞬态运行工况,也是发动机空燃比控制的难点。本文在瞬态工况中采用上述空燃比闭环控制器,通过对空燃比进行精确控制,防止发动机在瞬态工况下,排放性能变差。
为了验证本文算法的效果,将两种算法在节气门突变的情况下进行对比。
如图5所示,第一种算法是在PID的基础上加上前馈控制,第二种是RBF神经网络控制策略。在稳态工况下两种控制策略都有小幅波动,但都在稳定范围内。当节气门由20%突变至48%时,第一种算法在3.25秒后重新趋于稳定,且最大过量空气系数达到了1.24;第二种算法达到稳态耗时约0.7秒,最大过量空气系数为1.12。由此可知本文使用的RBF神经网络算法比PID算法重新回到稳态的时间明显更少,且由于对空燃比预测时充分考虑了系统延时,空燃比控制误差也有效降低。
如图6所示,节气门开度突然从36%降低至28%时,发动机转速由原来的稳定在1900r/min在3s内降至1200r/min,并保持稳定在1200r/min左右。RBF神经网络控制的空燃比在节气门突变后的0.8s内有剧烈波动,之后也稳定在预设空燃比附近。

图5 两种控制策略效果对比图
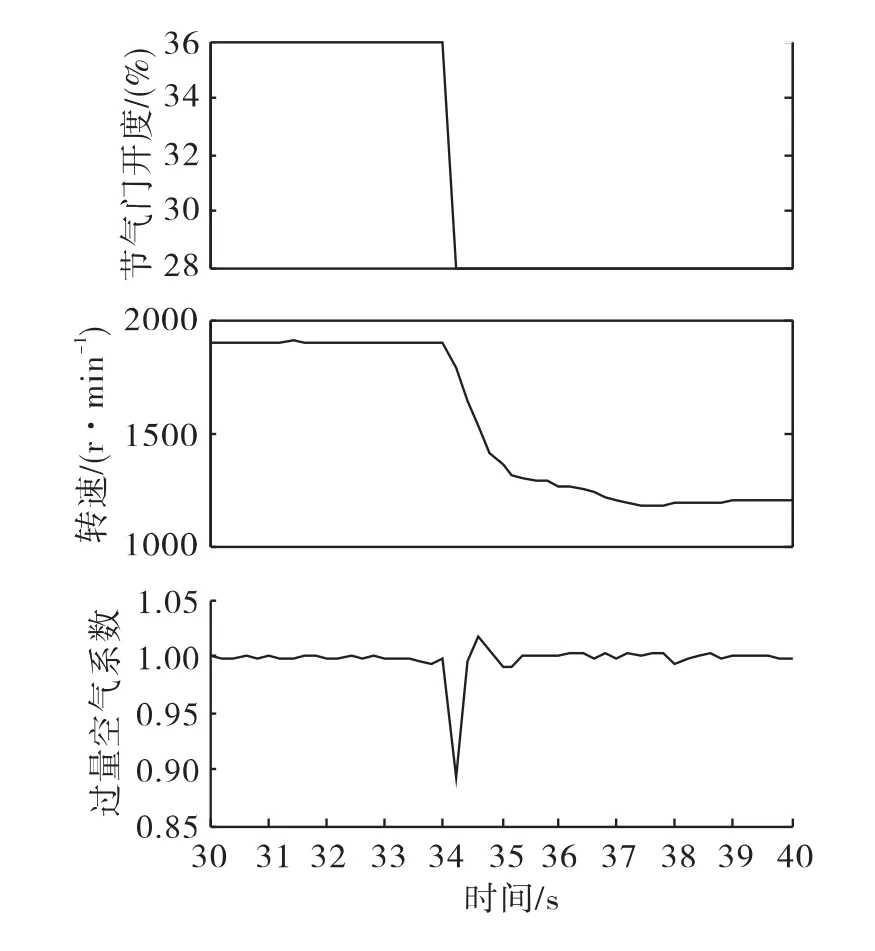
图6 节气门突降转速及过量空气系数变化
图7为节气门开度由28%升至36%时发动机转速变化和过量空气系数变化情况,此时过量空气系数目标值是1。由图可见,发动机转速在约2.8s后稳定在1900r/min左右,空燃比系数也有大的波动,在1s左右恢复稳态。
由以上的分析可知,RBF神经网络控制的空燃比在工况突变时能够即快速又准确地恢复到初始给定值。这说明在工况突变的过程中,前馈控制结合经过RBF神经网络预测的空燃比信号,通过PID闭环控制,可以使发动机的空燃比随着工况变化的波动尽可能的小,从而防止瞬态工况的排放性变差。
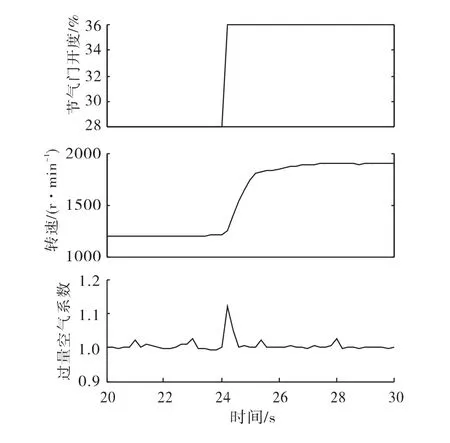
图7 节气门突升转速及过量空气系数变化
5 结论
本文分析了电喷天然气发动机产生延迟的因素,并建立RBF神经网络电喷天然气发动机的仿真模型,在工况突变的各个情况下进行仿真实验。实验结果表明,与普通PID算法相比,在瞬态工况下能有效缩短过渡时间,降低了空燃比超调量,提高了系统瞬态工况下的动态性能及空燃比控制精度。
1 孟嗣宗,郭少平,张文海.发动机精确空燃比控制方法的研究[J].内燃机工程,1999(2):70~75
2 Clarke D W.Application of generalized predictive control to industrial processes[J].IEEE Control System Magazine,1998,122:49~55
3 席裕庚.预测控制[M].北京:国防工业出版社,1993
4 郑海兵.广义预测控制改进算法的仿真研究[D].大连:大连理工大学,2008
5 Clarke D W,Mohtadi C,Tuffs P S.Generalized predictive control- part I..the basis algorithm[J].Automatica,1987,23(2):137~148
6 刘亚斌,刘雪田,肖文晖.基于改进Elman神经网络的燃气管网实时预测[J].系统工程学报,2003,18(5):475~478
