自适应高斯混合模型及说话人识别应用*

王韵琪，俞一彪

(苏州大学 电子信息学院，江苏 苏州 215006)

0 引言

说话人识别是利用说话人的语音特征鉴别或确认说话人的身份，广泛应用于需要身份安全认证的领域。其主要方法有支持向量机(SVM，Support Vector Machine)［1］和高斯混合模型(GMM，Gaussian Mixture Model)［2］等。由于高斯混合模型GMM对语音声学特征分布有较好的拟合特性，基于最大似然决策的GMM方法已经成为说话人识别系统的主流方法［3］。但是，传统GMM方法中每个说话人的模型结构完全相同，高斯分量混合数是固定一致的，这样会导致在每个说话人语音特征参数分布聚类特性不同时出现模型过拟合或者欠拟合的现象。实际应用中，每个说话人的发音特点不同，甚至有的带有天然的口音和发音异常，因此语音声学特征参数的统计分布不仅不同，而且其聚类特性也不相同。所以，采用固定的高斯分量混合数并不符合实际，同样的模型结构无法保证适合于每一个说话人，而模型拟合的精确性将会严重影响系统的识别性能。因此，应该根据说话人的具体语音特征分布来选择混合数并建立相应的模型，使每个模型更好地拟合每个说话人的具体特征分布。

本文提出一种新的自适应高斯混合模型AGMM统计分析方法应用于说话人识别。自适应高斯混合模型AGMM的结构根据说话人特征参数实际分布来确定，其高斯分量混合数在训练过程中动态确定而不是事先设定，从而能解决传统GMM方法的过拟合和欠拟合问题。本文建立了40个说话人的文本无关辨认系统，分别使用BFCC［4］参数和MFCC参数在不同的测试语音长度下对提出的新方法进行了实验，结果证明本文提出的AGMM能够有效提高识别性能。

1 系统结构

完整的说话人辨认系统结构如图1所示。

图1 说话人辨认系统结构框Fig.1 Block diagram of speaker identification

说话人语音模型采用本文提出的自适应高斯混合模型AGMM。由M个高斯概率密度函数加权求和得到的传统GMM如下表示:

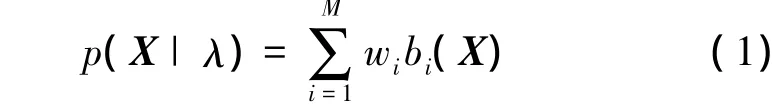
式中，X是一个D维随机向量;wi，i=1～M是混合权重，满足

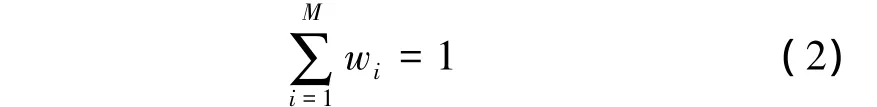
bi(X)，i=1～M是子分布，可表示为

式中，μi是均值向量，Σi是协方差矩阵。

本文提出的自适应高斯混合模型AGMM与传统GMM的区别主要在于混合数M的不同。传统GMM设置了固定的高斯分量数，而AGMM根据每个人的具体语音特征分布采用了可变的混合数，能够很好地解决模型拟合中出现的过拟合或者欠拟合问题，提高系统识别性能。模型的具体训练算法见第3节。

特征参数采用16阶BFCC。BFCC是依据新的双线性频率变换尺度(Bilinear Frequency Scale)提取出的［4］。该频率尺度与原始频率的对应关系表现为一条类似双线性变换曲线，在低频段和高频段上升较快，而中频段上升平缓。文献［4］计算得到其变换公式，如式(4)所示:

图2是在纯净语音环境下，特征参数BFCC与传统Mel尺度变换提取出的MFCC误识率比较图。由于主要观察分析特征参数的性能，说话人模型采用的是16个分量的传统GMM模型［5］。关于传统GMM的不同分量数条件下说话人识别性能的影响很多研究工作者在以往的实验中都进行过分析，得出的结论是16分量是一个合理的选择［5］。

图2 BFCC与MFCC误识率比较Fig.2 Error accuracies with BFCC and MFCC

从图2中可以明显看出，特征参数BFCC识别率相比MFCC提高幅度较大，而且参数BFCC在4 s时误识率已经降到了0，说明新的双线性频率变换尺度相对于传统的Mel频率尺度更适合应用于说话人识别系统。

2 自适应高斯混合模型

传统GMM方法中运用了固定不变的混合数，这并不符合说话人语音特性分布多样性的实际情况。实际应用中，某些说话人的语音特征分布中高斯子分量比较稀疏，而有些则比较丰富，因此，采用固定混合数结构缺乏合理性。虽然可以通过权重来调节高斯子分量的影响，但仍然会在模型训练中导致过拟合或者欠拟合的现象出现。因此，应该根据每个说话人具体的语音特征分布确立模型结构并建立相应模型，保证模型更加精确地拟合每一个说话人的具体特征分布。

2.1 模型训练算法

在AGMM的训练中，依据当前各高斯分量的权重、均值和方差进行综合分析，采取吸收合并与分裂机制动态地调整高斯混合数。若某一高斯分量的权重很小，且与其他分量有一定距离，则可以认为这个分量反映了稀少的孤立性信息，甚至是噪声信息，因而没有实际价值，可以消除这一分量，其包含的样本将由其他分量进行吸收;若两个高斯分量距离很近且权重不大，则认为这两个分量反映相同的特征分布，可以合并形成一个高斯分量;若高斯分量的权重很大且其至少某一维的方差也很大，则说明此分量包含了过多的分散性样本，会导致拟合不精确、出现欠拟合现象，可以采用分裂处理将其分裂为两个高斯分量。

具体训练步骤如下:

Step 1:设置AGMM初始混合数K，允许EM训练的次数 H，以及阈值 αt1，αt2，αt3，Dt，σt;

Step 2:利用K－means算法初始化高斯分量均值、方差与权重;

Step 3:运用EM算法训练模型，训练次数加1;若是最后一次训练，跳到Step 7，否则顺序执行;

Step 4:对于训练得出的模型，若某一分量(wi，μi，Σi)的权重小于阈值αt1，说明这个分量没有实际价值，需要消除，用其最近分量(wj，μj，Σj)对这个分量进行吸收，吸收按照以下处理:

这样，形成一个新的高斯分量为:(wk，μk，Σk)。混合数K=K－1，返回Step 3进行新一轮EM训练;

若满足吸收的分量不止一个，则按权重从小到大的顺序选择最小的分量进行处理。

Step 5:若某一分量(wi，μi，Σi)与最邻近分量(wj，μj，Σj)之间的距离小于阈值 Dt且权重小于αt2时，说明此分量与最近邻分量相距很近且包含的信息较少，将这两个分量合并，按照以下处理:

两个高斯分量之间的距离用如下公式计算:

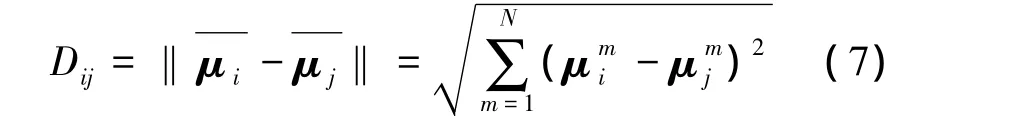
式中，N=1～24为特征矢量的维数。

通过以上处理形成一个新的高斯分布为(wk，μk，Σk)。混合数 K=K－1，返回 Step 3 进行新一轮EM训练;

若满足合并条件的分量不止一个，则按距离从小到大的顺序选择最小距离的分量进行合并。

Step 6:若某一分量(wi，μi，Σi)权重大于阈值αt3，且至少有一维的方差大于σt时，说明这个分量包含了太多的信息，可以将此分量分裂，处理如下:

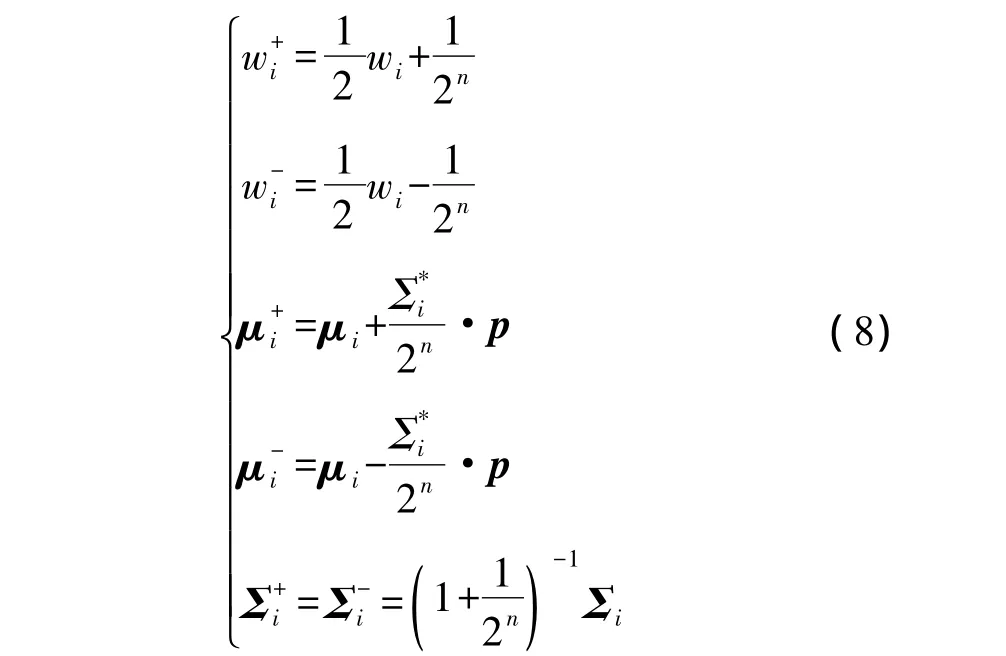
若满足分裂条件的分量不止一个，则按权重从大到小的顺序选择最大的分量进行分裂。

Step 7:训练终止，得自适应高斯混合模型AGMM。

算法的初始混合数K一般可取16，EM训练次数H取10，其他的权重、方差和距离阈值与实际采用的特征参数及其维数存在关联，需要通过预实验分析获取合适的值。

2.2 模型训练实例分析

图3、图4分别是AGMM训练迭代过程中合并和分裂处理前后高斯分布的变化图。由于空间局限性，图中只画出了第一维特征参数的分布情况。

图3 第32个说话人AGMM训练中的合并处理Fig.3 No.32speaker’s merge processing in AGMM training

由图3(a)和图3(b)可以看出AGMM进行了合并处理，把权重较小的第2个高斯分量和与之相近的第3个高斯分量合并成了新的第2个高斯分量。实验中发现，在测试语音长度为1s时，此人采用传统GMM的误识率为9.75%，而用AGMM的误识率为3.58%，说明了合并处理使得拟合性能更加优越并且提高了识别性能。

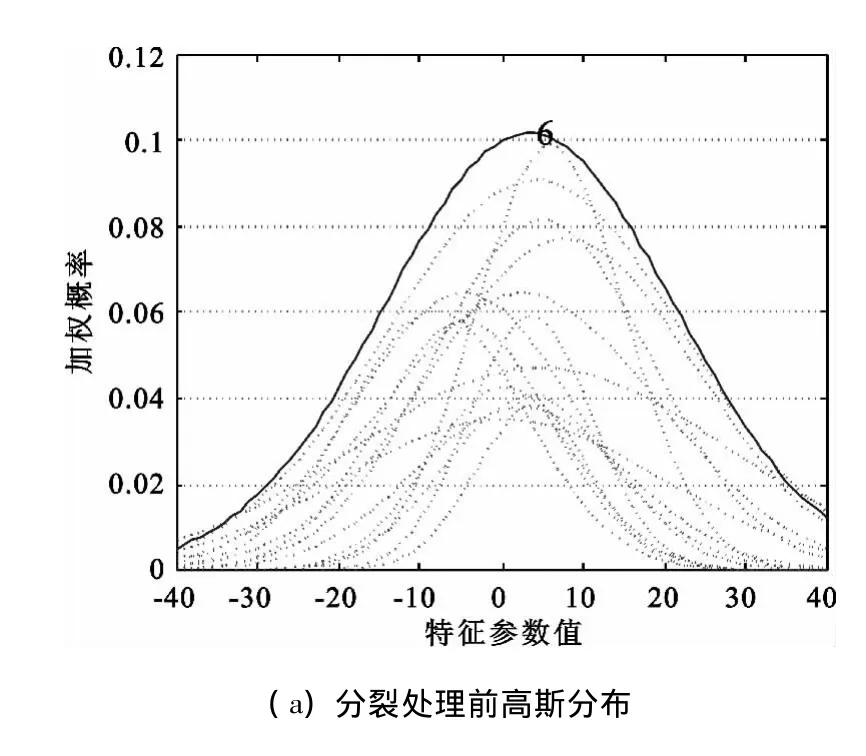
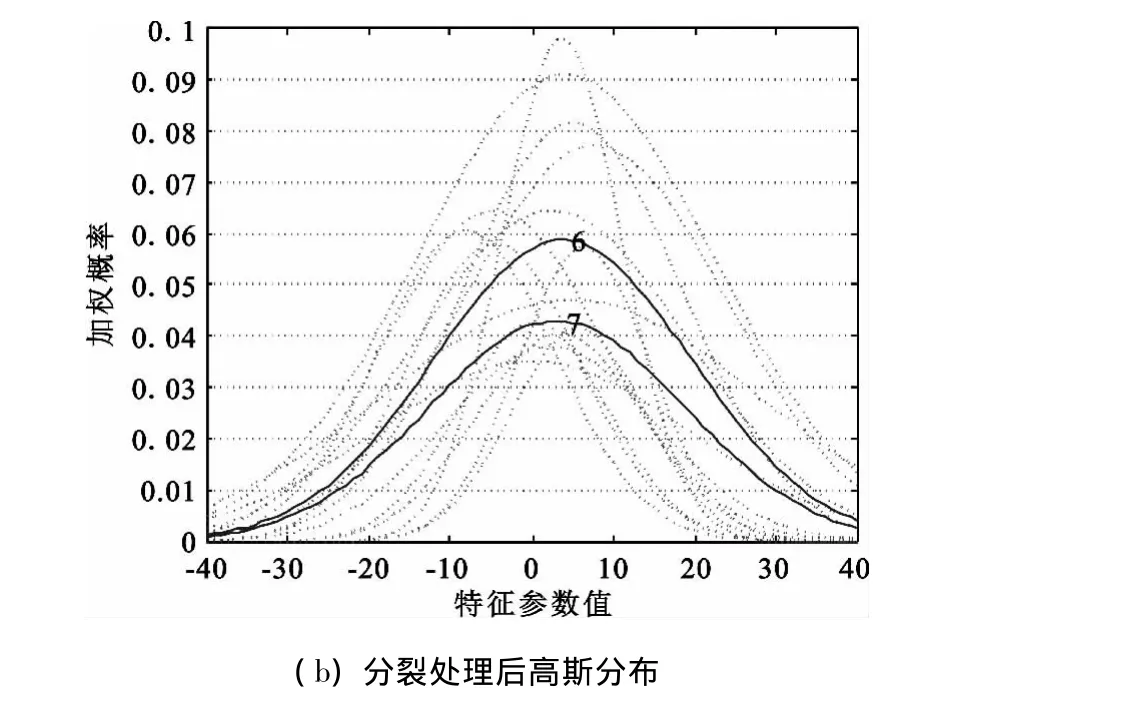
图4 第17个说话人AGMM训练中的分裂处理Fig.4 No.17 speaker’s split processing in AGMM training

由图4(a)和图4(b)对比可知第6个高斯分量由于权重和方差过大，包含的样本过多，分裂成第6和第7个高斯分量。实验中，在测试语音长度为1s时，采用传统GMM的误识率为1.5%，而用AGMM的误识率为0，说明分裂处理有利于提高模型拟合精度和识别性能。

图5给出了系统中40个说话人AGMM的高斯混合数分布图。

图5 高斯混合数分布Fig.5 Distribution map of Gaussian mixture number

由图5可知，并不是所有的说话人的AGMM都需要进行吸收合并和分裂。40个说话人模型中24个保持了16个高斯分量混合数不变，另外16个通过吸收合并与分裂改变了高斯分量混合数。总体上，AGMM可以有效地克服过拟合和欠拟合现象，提高系统识别性能。例如，第2个说话人在测试语音为1s时，采用GMM有4段语音误识成他人的语音，而AGMM只有1段语音误识成他人语音，而第16个说话人采用GMM时，1s测试语音中有1段语音误识成他人的语音，采用AGMM之后没有语音误识成他人语音。

3 识别实验与分析

3.1 实验环境与预处理

实验中语音数据取自SUDA2002－D2数据库。该数据库包含40个说话人的普通话语音，均在普通实验室环境下用普通声卡进行录制，采样率11025 Hz，量化精度为16位。40人中男生25人，女生15人，每个人录制了7段12s的语音，前4段用于训练，后3段用于识别。实验中，每个说话人采用本文提出的算法训练自适应高斯混合模型AGMM，其高斯分量的初始取值K为16，各个阈值的取值为:αt1=0.025，Dt=7.000，αt2=0.040，αt3=0.084，σt=10.000，H =10。

3.2 实验结果与分析

实验采用特征参数BFCC和MFCC，在不同测试语音长度下分析了AGMM方法的有效性，并与传统GMM方法进行比较。采用如下公式来计算AGMM相对于传统GMM的误识率下降程度:式中，mi代表AGMM误识率，ni代表传统GMM误识率，Ri代表相对提高程度，i=1～5代表测试语音长度。

3.2.1 MFCC参数下的比较分析

图6是AGMM和传统GMM分别在MFCC参数下，系统的误识率随不同长度测试语音的变化图。

图6 MFCC参数下误识率比较Fig.6 Error accuracies of the two models with MFCC

从图6中可以看出，AGMM的误识率在不同测试语音长度下都比传统GMM要低，这表明采用吸收合并与分裂的模型自适应处理方法是有效的。表1列出了各测试语音长度下误识率的具体值，可以看出相对GMM，本文提出的AGMM的误识率平均下降了41.41%，效果非常明显。

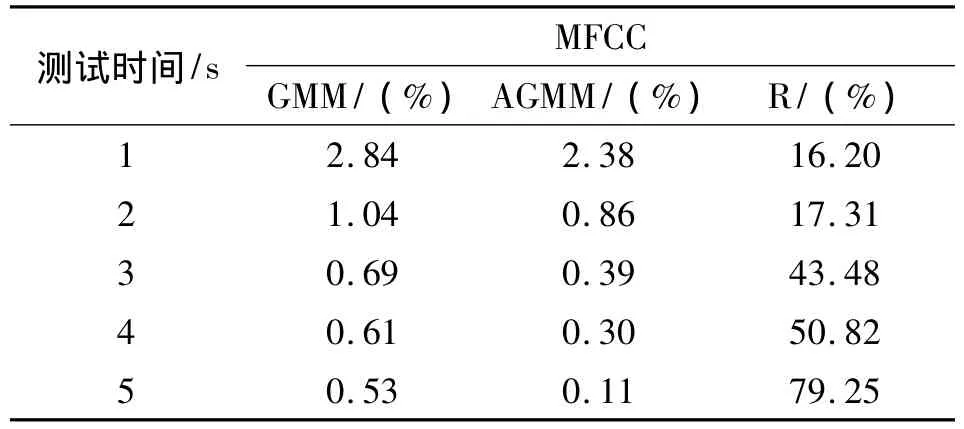
表1 MFCC参数下性能提高程度Table 1 Improve accuracy compared to two GMMs with MFCC

3.2.1 BFCC参数下的比较分析

图7是BFCC参数下，AGMM和传统GMM在不同的训练语音长度下系统的误识率变化图。

图7 BFCC参数下误识率比较Fig.7 Error accuracies of the two models with BFCC

从图7中可以看出，不同测试语音长度下AGMM的误识率同样比传统GMM要低。由于BFCC的性能比MFCC优越，采用GMM已经能够得到较好的识别性能，因此，当采用AGMM时其误识率下降不如在MFCC参数下明显。

表2给出了各个测试语音长度下两种模型的误识率具体值，相对GMM，本文提出的AGMM平均误识率下降了22.21%。

表2 BFCC参数下性能提高程度Table 2 Improve accuracy compared to two GMMs with BFCC

4 结语

本文提出了自适应高斯混合模型AGMM，优化了说话人语音特征参数统计分布的拟合性能。AGMM是在传统GMM基础上采用自适应策略调整模型混合分量数得到，因此两者性能的比较是在统一基准条件下进行。本文采用说话人识别中常规的16分量为基准进行分析比较。从实验结果来看，可以有效地克服传统GMM方法的过拟合和欠拟合问题，通过算法提供的吸收合并与分裂机制找到一个更加合理的模型阶数，提高系统的识别性能，其误识率明显低于传统GMM方法，说明本文提出的方法是有效的。当然，AGMM的训练相对传统GMM需要更多的时间，但平均来说并不大，而识别阶段没有任何影响。本文提出的自适应高斯混合模型AGMM对信号处理其他应用领域同样具有参考价值。今后，将进一步针对信道差补偿以及噪声环境下的鲁棒性识别问题进行研究。

［1］CUMANI S，LAFACE P.Analysis of Large－Scale SVM Training Algorithms for Language and Speaker Recognition［J］.IEEE Trans.on AUDIO，SPEECH，AND LANGUAGE PROCESSING，2012，20(05):1585－1596.

［2］SELVA N S，SELVA K R.Language and Text－independent Speaker Identification System Using GMM ［J］.WSEAS Trans.On Signal Processing，2013，9(04):185－194.

［3］赵振东，张静，李圆，等.基于GMM说话人分类的说话人识别方法研究［J］.通信技术，2009，42(10):192－193.ZHAO Zh.D.，Zhang J.，Li Y.，et al.Speaker Recognition Research Based on GMM Speaker Clustering Technology ［J］.Communications Technology，2009，42(10):192－193(in Chinese)

［4］俞一彪，袁冬梅，薛峰.一种适于说话人识别的非线性频率尺度变换［J］.声学学报，2008，33(05):450－455.YU Y.B.，YUAN D.M.，XUE F..A Nonlinear Frequency Scale Conversion of Speaker Recognition［J］.ACTA ACUSTICA，2008，33(5):450－455(in Chinese)

［5］REYNOLDS D A，ROSER C.Robust Text－independent Speaker Identification Using Gaussian Mixture Speaker Models［J］.IEEE Transactions on Speech and Audio Processing，1995，3(01):72－83.