三体船总振动简化预报研究
2014-10-30王显正刘见华
王显正,刘见华
(中国船舶及海洋工程设计研究院,上海 200011)
0 引 言
三体船型是近年来发展的一种新船型,其结构形式与常规船有很大差别,关于船型设计和波浪载荷的研究已有不少[1~3],但对总振动模态的相关研究极少。三体船呈现出有别于常规船型的复杂振动特性, 具有垂向振动、水平振动、横向弯曲振动以及纵、横向扭转振动等多种振动模态,有些振动模态和单体船、双体船类似[4,5],有些则是三体船独有的。三体船型的振动模态只有采用三维有限元计算法才能比较准确地计算。整船三维有限元模型采用板、梁单元来模拟整个船体结构,是最接近真实船体结构的一种模型,对各种振动模态的分析比较准确,但需要船体结构的详细设计信息,且工作量很大。在早期设计阶段,往往会进行多种结构设计方案的比较分析,不具备进行全船有限元振动预报的条件,但又需要快速的预报全船振动模态,以判断结构设计方案是否合理,因此在早期设计阶段有必要研究一种估算方法,在满足一定工程精度的前提下能够快速进行三体船总振动固有频率预报,以满足方案论证的需求。
针对某型三体船进行总振动分析,先采用三维有限元法进行预报,再采用迁移矩阵法进行简化预报,探讨了三体船模态计算时的片体刚度缩减[6]。通过对迁移矩阵法及三维有限元法计算结果的比较,对早期设计阶段提出了三体船总振动特性预报。
1 三维有限元法
1.1 模型建立
全船有限元计算模型采用MSC/PATRAN建立。有限元模型包括本体、片体、连接桥结构和第一层上层建筑的所有甲板、外板、平台、横舱壁、强框架等。船体结构有限元网格横向按纵骨间距划分,纵向按肋骨间距划分,舱壁按骨材间距划分。所有板构件均以SHELL单元模拟,且大部分为四边形单元,仅在一些过渡区域采用了部分三角形单元。其他构件直接采用beam单元模拟、考虑偏心影响,支柱采用beam单元模拟。有限元模型模拟全船的实际重量、重心和质量惯性矩,将模型分成若干部分,并通过调整各部分的材料密度模拟钢料和小设备的质量。全船的大设备、压载水等采用质量单元模拟,质量单元建在相应的结构上,并考虑偏心的影响。全船有限元模型总计有34242个节点,83276个单元(见图1)。
船舶整体振动时,船舷外有部分流体与船体湿表面耦合一起振动,因此需对船体水线以下湿表面单元添加附连水质量。在采用MSC /Nastran进行船体振动计算时,舷外附连水质量在Nastran程序中通过定义湿表面及吃水自动添加,其原理为按源汇分布计算流固耦合。
1.2 边界条件
对于分析计算结构物自由振动,MSC/Nastran程序具有悬浮体模型计算功能,可以不施加任何约束,模拟船舶在水中自由振动的状态,因此,在船体结构自由振动和模态分析计算中,不需要施加任何边界条件,即整个模型为自由体。

图1 全船有限元模型
1.3 自由振动计算及结果分析
通过全船有限元振动计算分析,可以得到全船船体各阶振动振型和频率。图2~8为各阶振动振型图,计算值见表1。由结果可见,三体船的前三阶垂向振动和一阶水平振动模态和单体船类似,纵向扭转振动比单体船明显,而片体和连接桥耦合的横向弯曲振动和横向扭转振动模态为三体船所独有,与双体船相比既有部分类似又有很大区别。后几种振动模态用船体梁法无法预报,只有采用三维有限元方法才能比较准确地计算并获得预报。

图2 一阶垂向弯曲振动

图3 二阶垂向弯曲振动

图4 三阶垂向弯曲振动

图5 一阶水平弯曲振动

图6 纵向扭转振动

图7 片体及连接桥结构横向弯曲振动

图8 片体及连接桥结构横向扭转振动

表1 总振动计算频率
2 迁移矩阵法
严格而言,三体船剖面与铁木辛柯梁有一定差异,但三体船主体较细长,如考虑将片体刚度合并到主体内则可将全船近似简化为一根细长梁,进而采用迁移矩阵法计算。因存在剪切迟滞效应,常规船在高阶振动计算时剖面惯性矩应乘以相应的减缩系数,但目前世界上的三体船实船较少,尚无法进行统计归纳,故采用类似方法对三体船剖面刚度的减缩进行探讨,主体的刚度按100%计入,片体刚度按100%、50%、0%三种情况计入。三体船布局特殊,主片体附连水相互间有影响,与主片体尺寸、间距有关,但三圆柱体附连水质量的研究结果[7,8]显示在一定条件下可以不考虑主片体之间的相互干扰,因此主体、片体附连水按刘易斯法100%计入(见表2)。
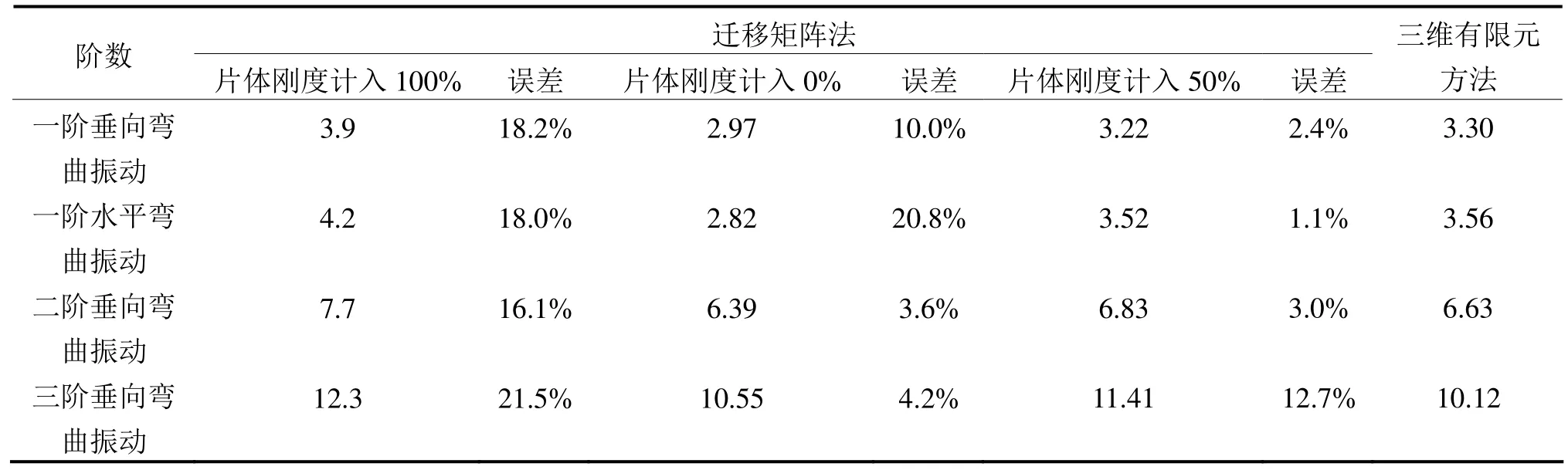
表2 总振动计算结果及比较 Hz
3 对比分析
将三体船[9]分别采用迁移矩阵法和三维有限元法得到的计算结果进行比较,可见片体刚度100%计入时各阶计算值都明显偏高;片体刚度计入 0%时计算值一阶偏低,高阶符合较好;片体刚度计入 50%时计算值一阶符合较好,高阶偏高。
4 结 语
1) 三体船呈现有别于常规船型的复杂的振动特性,有些与常规船[10]类似,有些则是三体船独有,这些不同于常规船型的振动特性只有采用整船三维有限元法才能计算得到。
2) 在设计的早期阶段,可将片体刚度合并至主体中,再采用迁移矩阵法进行预报,片体刚度在计算一阶模态时可按50%计入,高阶模态时可忽略不计,可快速进行三体船振动模态的预报,同时预报误差可控制在较小范围内,有利于设计的早期阶段进行结构设计方案论证分析。
[1] 谭 美,林 一,李 平. 基于AHP的三体巡视船概念设计研究[J]. 上海造船,2011(1):21-25.
[2] 朱东华,刘见华. 高速三体船结构设计问题[J]. 船舶,2010(1):30-33.
[3] 吴帆行,刘见华,黄守成. 三体船垂向波浪载荷预报[J]. 船舶,2008(6):13-18.
[4] 郑 豪,郭 列. 双体穿浪船船体振动特性分析[J]. 中国造船,2006,47(1):90-93.
[5] 李 强,王慧彩,等. 小水线面双体船船体总振动固有频率预报研究[J]. 船舶,2009(4):20-24.
[6] 金咸定,赵德有. 船体振动学[M]. 上海:上海交通大学出版社,2000.
[7] 董 威,吴卫国,徐双喜,等. 三圆柱体附连水质量的数值计算[J]. 中国舰船研究,2009 (4):34-36.
[8] 程 虎,吴卫国,李晓彬,等. 基于ANSYS的三圆柱附连水质量计算[J]. 交通科技,2011 (5):104-106.
[9] 张洪达. 712各位三体客货运输船总体设计[J]. 船舶与海洋工程,2013, (2): 23-27.
[10] 雷 坤. 39000dwt散货船总振动分析[J]. 船舶与海洋工程,2013, (4): 19-22.
