成都地区砂卵石场地锚拉桩支护结构嵌固段深度的探讨

王君红，付彬桢，高晨光，王 宁

(中国建筑西南勘察设计研究院有限公司，四川成都610052)

利用有限元软件plaxis通过对成都地区砂卵石场地某典型深基坑工程支护桩在不同嵌固段深度情况下桩的变形、弯矩、稳定性及塑性区分布并进行分析，对此类场地多支点锚拉桩支护结构嵌固段深度进行探讨。

1 工程概况

某工程位于成都市锦江区新光华街1号，西临人民南路，东临光华街，南临新光华街，北接皇城公寓，紧邻地铁一号线。拟建建筑物基础埋深约－20.00 m，周边环境对基坑变形极为敏感。基坑周边位置平面关系见图1。

图1 基坑周边位置关系平面图

基坑安全等级为一级，基坑－4.0 m以上采用坡度系数为0.2的放坡，－4.0 m以下支护型式为锚拉桩支护。桩径φ取值为1 000 mm，桩间距3.00 m，有效桩长20.00 m，嵌固深度4.0 m，冠梁为1 000 mm×800 mm，其水平侧向刚度系数为0。在－7 m、－12 m、－16 m 处设置3层预应力锚索(φ130，内灌浆，长度分别为16.0 m、13.0 m、12.0 m，锚固段分别为11.0 m、9.0 m、8.0 m)，锚索锚固于支护桩身上，不设腰梁。配筋计算与锚杆(索)计算均根据相应规范进行。稳定性验算仅进行了整体稳定性验算与抗倾覆稳定性验算，整体稳定性验算计算方法采用瑞典条分法。

2 地质情况

根据该工程勘察报告可知，场地内钻孔揭露地层为第四系全新统的人工填土(Qml4)、第四系全新统冲积层(Qa14)的粉质黏土、粉土、砂土和卵石土及白垩系灌口组泥岩(K2g)。土层结构由上而下划分为:

(1)杂填土:以建筑垃圾为主，夹较多混凝土块及卵石，层厚2.20～4.10 m。

(2)粉质黏土:灰黄色，可塑，稍湿，层厚0.40～1.30 m。

(3)粉土:黄灰色，中密，稍湿，层厚0.60～1.90 m。

(4)细砂:灰色、黄灰色，松散，层厚0.30～2.00 m。

(5)中砂:灰色、黄灰色，松散，该层呈透镜状分布于卵石层中。

(6)砾砂:杂色，湿～饱和，成份以细～中砂为主，该层呈透镜状分布于卵石层中。

(7)圆砾:细中砂充填，部分泥质充填。

(8)卵石:杂色，湿～饱和，细、中砂充填，部分泥质充填，局部夹中砂、粉土透镜体。卵石层顶面埋深3.10～4.70 m，划分为:圆砾、稍密、中密、密实卵石层。

(9)泥岩:紫红色、灰绿色泥岩，稍湿，夹泥质粉砂岩透镜体，该层顶面埋深 22.20～23.50m，顶面高程 477.31～478.06 m，依风化程度分为强风化带与中风化带。

3 模型的建立

3.1 网格生成

根据基坑的平面形状、开挖深度和地质条件等因素，X向范围77.0 m，Y向深度至深－35.0 m。模型土体选用15节点三角形单元模拟，支护桩采用梁单元模拟，锚索自由端采用点对点锚杆模拟，锚固段采用土工格栅模拟;工程桩与土体之间采用Goodman接触面单元模拟两者之间的相互作用。

3.2 本构模型及参数选择

选取基坑边中部一典型剖面，根据场地综合地质情况将土层划分为5层，分别为杂填土、中砂、卵石、强风化泥岩及中风化泥岩，岩土材料按Mohr－Coulomb材料考虑，岩土材料参数见表1;支护桩、锚索及土钉采用线弹性模型，计算参数见表2和表3。

表1 岩土材料参数

表2 支护桩计算参数

表3 锚索及土钉计算参数

3.3 荷载及边界条件

根据周边环境在距基坑边9.6 m、深度3 m处布置一局部均布荷载q=100 kN/m2。取几何模型的上边界为自由边界，在几何模型底部施加完全固定约束，在两侧竖直的边界施加滑动约束。建成后的PLAXIS网格模型见图2。

图2 PLAXIS网格模型

3.4 计算工况

水压、变形、地应力场等初始条件设置后，根据基坑开挖和支护的施工工序，计算共考虑了10个工况(预加力为实测锚索拉力)。

3.5 不同嵌固段深度计算结果分析

通过调整不同嵌固深度对桩身变形、桩身弯矩、整体稳定性以及塑性区分布的影响进行分析。选取的嵌固深度为0.2H、0.15H、0.1H、0.01H 及无嵌固段。

3.5.1 桩身变形

图3为不同嵌固深度情况下计算得到的桩身水平变形。

由计算结果可知:

(1)随嵌固深度的减小，桩身整体向坑内滑移趋势增大，桩身水平变形的形状由弧线型变为直线型，桩身顶端变形变化幅度较桩身中下部变形变化幅度小，表明随嵌固深度的减小，基坑的变形模式由规范的深层滑动模式向浅层倾覆模式转变;

图3 不同嵌固深度桩身水平变形

(2)桩身水平变形最大值随嵌固深度的减小而先减小后增大，当嵌固深度为0.05H和0.1H时，桩身水平位移基本未发生变化，最大变形位置始终处于桩顶;无嵌固段与0.2H比较，桩身最大变形仅增大了5.6 mm，表明对锚拉桩支护结构其稳定性是抗倾覆的控制作用更为明显。

3.5.2 桩身弯矩

图4为不同嵌固深度情况下计算得到的桩身弯矩。

图4 不同嵌固深度桩身弯矩

计算结果表明:桩身负弯矩最大值随嵌固深度增大而增大，且其变化幅度随深度增大也是越大，在有嵌固段时其位置始终处于14.0 m左右，无嵌固段时整个桩身仅两端有较小的负弯矩作用，与锚杆支护结构弯矩分布模式近似，表明规范受力和变形分析模型不能完全适用砂卵石场地锚拉桩支护结构的基坑工程设计。

3.5.3 整体稳定性

图5为不同嵌固深度情况下采用强度折减法计算得到的整体稳定性安全系数。

图5 不同嵌固深度整体稳定性安全系数

计算结果表明:不同嵌固深度对基坑整体稳定安全系数的影响较小，其值位于2.0～2.1之间，均大于规程要求的1.2，表明嵌固段对整体稳定性影响不明显，规程整体稳定性验算方法显然不适用于砂卵石场地基坑，即规范对锚拉桩满足稳定性要求的前提下仍须按0.2H长度设置桩的嵌固深度的要求不尽合理。

3.5.4 塑性区分布

图6～图10为不同嵌固深度塑性点分布图。

图6 嵌固深度0.2H塑性点分布

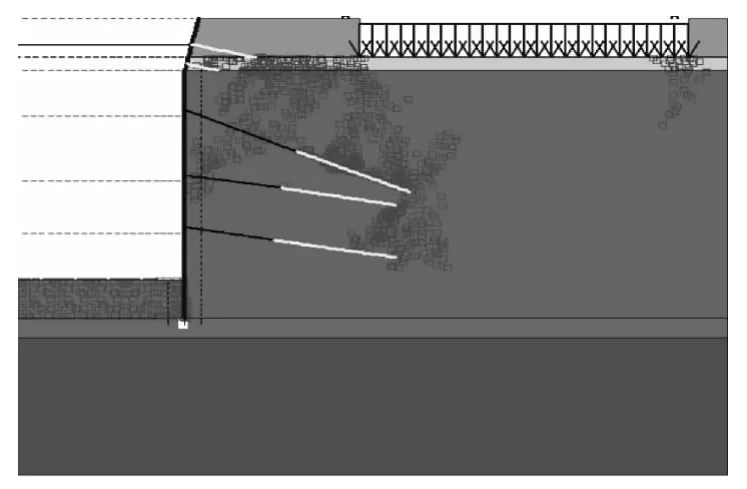
图7 嵌固深度0.15H塑性点分布

计算结果表明:

(1)按照规程要求嵌固段深度取0.2H时，桩后土体形成一条沿第二道锚索锚头位置至附加荷载角部未贯通塑性破坏区及附加荷载角部至第一道锚索锚固段末端的贯通的塑性破坏区，塑性破坏区主要分布在第二道锚索位置以上;

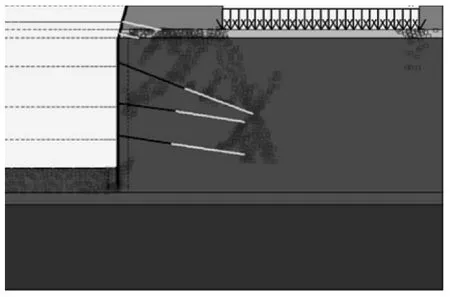
图8 嵌固深度0.1H塑性点分布

图9 嵌固深度0.05H塑性点分布

图10 无嵌固段时塑性点分布

(2)在嵌固段深度为0.15H时，第二道锚索锚头位置至附加荷载角部的塑性破坏区贯通，同时附加荷载角部至锚索锚固段末端的塑性破坏区沿原方向向下延伸至第三道锚索锚固段末端，第一道锚索上部土体塑性区扩大;

(3)当嵌固段深度减小为0.1H时，原第二道锚索锚头位置至附加荷载角部的塑性破坏区贯通方向逐步转变为自桩底朝向附加荷载角部，且在桩底附近形成沿次方向的一段较小塑性破坏区，沿附加荷载角部与锚索锚固段末端的塑性破坏区及上部塑性破坏区基本未发生变化;

(4)在嵌固段深度为0.05H时，由桩底至附加荷载角部方向的塑性破坏区沿此方向延伸但未贯通，沿附加荷载角部与锚索锚固段末端的塑性破坏区及上部塑性破坏区基本未发生变化;

(5)当无嵌固段时，自桩底至附加荷载角部方向形成一贯通塑性破坏区，此破坏区与水平面大致成58°角，而其余部分塑性破坏区并未发生太大变化。

4 结论

(1)通过对砂卵石场地不同嵌固深度的模拟，能够较为真实的了解不同嵌固深度下基坑稳定特征及支护结构变形和受力特性，为今后在此类场地进行支护结构合理设计提供依据。

(2)不同嵌固深度对基坑整体稳定安全系数和桩身水平最大变形的影响较小，嵌固段对整体稳定性影响不明显，桩身弯矩随嵌固深度增加而显著提高。对此类场地规程设计方法构造要求嵌固深度0.2H在一定程度上讲“有害无益”，因此，规程整体稳定性验算方法显然不适用于砂卵石场地基坑。

(3)在无嵌固段时，桩身变形及桩身内力与锚杆支护结构中的肋柱近似，且整体稳定性和变形均在在规程规定的控制范围内，故笔者认为砂卵石场地锚拉桩支护结构可按照锚杆支护结构计算模式考虑。

［1］时伟，刘继明，章伟.深基坑桩锚支护体系水平变形试验研究［J］.岩石力学与工程学报，2003，22(增1):2335－2338

［2］JGJ 120－2012建筑基坑支护技术规程［S］

［3］候永茂，王建华，陈锦剑.超大型深基坑开挖过程三维有限元分析［J］.岩土工程学报，2006，28(增):1374－1377

［4］付先进，林作忠.基于plaxis的超深基坑开挖弹塑性有限元数值计算与分析［J］.中国水运，2010，10(4):190－192