模型和监控指标在混凝土重力坝健康诊断和预警中的应用

徐 荣

(江苏河海科技工程集团有限公司，江苏 泰兴225400)

大坝健康诊断和预警系统的建立，起步于模型的建立和监控指标的拟定，模型和监控指标作为大坝安全监测分析的重要方式，已经在众多安全监测系统中得到应用，但目前它们大部分仅被作为资料分析和预测的工具，本文旨在利用这两种工具，建立混凝土重力坝的健康诊断和预警体系。

1 建立模型

常规统计模型作为最常用的确定性模型，已经广泛应用于水利系统，特别是大坝安全监测领域，而不确定模型作为确定性模型的补充，可以考虑各种不确定因素，某些情况下可以弥补确定性模型因原始数据缺陷而导致的无法建模的不足，进而避免误诊和提高预警精度。

1.1 统计模型

观测变形、扬压力和渗流量所得的物理量是监测水工建筑物运行工况的重要量，因此主要针对这几个量来进行分析。位移统计模型因子较少，不需要计算前期环境量均值，而扬压力和渗流量统计模型导入信息时，不仅要记入降水量因子，还需要计算前期水位和降水量的均值。

1.1.1 位移统计模型

按成因，位移可分为3个部分:水压分量(δH)、温度分量(δT)和时效分量(δθ)，即:

对于混凝土重力坝，坝体在水压作用下产生位移的水压分量与大坝上下游水深的1 ～3 次方有关，故水压分量δH因子取h、h2、h3;考虑到有些坝的坝内温度计和水温资料不足、气温资料一般比较详实的情况，由于坝体混凝土内任一点的温度可以用周期函数标示，同时温度位移与混凝土温度呈线性关系，因此温度分量δT一般取多组谐波因子组合;大坝产生时效变形的原因极为复杂，它综合反映坝体混凝土与基岩的徐变、蠕变以及岩体地质构造的压缩变形等，因此时效分量δθ因子取δ 和lnδ。位移统计模型公式如下:

实际情况中，温度分量谐波因子组数和时效分量因子数可以变化。

1.1.2 扬压力统计模型

扬压力采用如下统计模型:

式中:Y 代表某扬压力测孔的扬压力测值，YHu为上游水位分量，YHd为下游水位分量，Yp为降雨分量，YT为温度分量，Yθ为时效分量。

例如，选择监测日前期水位平均值(1、2、5、10 d)作为水位分量因子;降雨分量亦取前期平均值(1、2、5 d)作为降水量因子;温度分量选取2 组谐波因子;时效分量的组成比较复杂，与库前泥沙淤积、扬压力监测孔周围的岩性、裂隙和构造分布及产状有密切的联系，故时效分量因子取δ 和lnδ。扬压力统计模型公式如下:

实际情况中，水位前期平均值天数可以为1，2，5，…，m 天，同样，前期降水量也可取1，2，5，…，n天，温度和时效分量因子个数也可改变。

1.1.3 渗流量统计模型

混凝土重力坝渗流量统计模型为:

式中:Q 为渗流量测值，QH1为上游水深分量;QH2为下游水深分量;QT为温度分量;Qθ为时效分量。

例如，上游水位变化对坝基渗漏量有很重要的影响，且有一定的滞后作用，重力坝下游水位影响可忽略不计，水位分量因子取前期水位平均值(2、3、4、5、6 d);降雨分量、温度分量和时效分量参考扬压力统计模型。最终的渗流量统计模型公式为:

实际情况中，各分量因子的选择同扬压力模型，根据实际条件变化。

1.2 不确定模型

不确定模型是由不确定信息建立的模型。常规统计模型的建立，需要各因子有确定的样本序列，而不确定模型则可以在缺少某种因子的条件下依旧可以建模，只不过它的精度随着建模因子的多少而变化，样本序列提供的自变量越多，建模结果越精确。常规的坝体性态分析方法，往往是基于某些确定的假设和认识，并运用各种确定的理论和方法来建立模型，这必然会在一定程度上降低模型的精确度。因此，对含有不确定参数的不确定大坝系统，利用不确定模型进行分析，可以较好的反映大坝的工作状态［1］。

1.2.1 位移不确定模型

位移不确定模型的自变量可以取3个，分别为日期、水位、温度;因变量为位移量。位移不确定模型的计算流程为:

自变量因子分别为u(水位)、v(温度)、t(日期)，因变量为w(表面变形)，则他们分别构成分析样本数据信息对(u，w)，(v，w)和(t，w)。原型观测资料中u、v、t 的信息分别对论域集W (变形集)、U(水位集)、V(温度集)和T(日期集)中各个控制点有不同的贡献，将各控制点从所有监测信息样本中得到的信息分别累加起来，便可得到原始信息分配矩阵Qi(i = 1，2，3)。对原始信息分配矩阵Qi分别沿纵横两方向作正规化处理，然后再对正规化处理后所得的两个矩阵作对应元素的取小运算，最后便可得各自变量论域集分别与因变量论域集合集之间的关系矩阵Ri(i = 1，2，3)，再根据式7 ～式9［2］:

式中:i =1，2，…n，步距△= αi+1－ αi

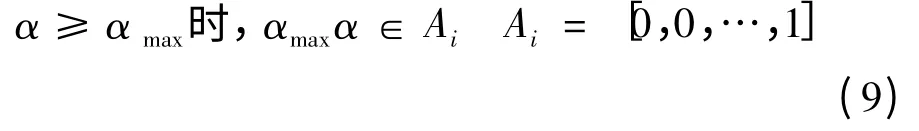
确定权重矩阵Au，Av和At，得到一级近似推理结果为:

那么待分析各自变量论域集分别与因变量论域集合集之间的综合近似推理结果为:

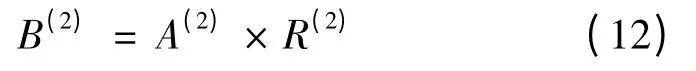
最终信息集中处理的结果为:

1.2.2 扬压力不确定模型

扬压力不确定模型的自变量可以取4个，分别为日期、水位、温度和降雨。

扬压力不确定模型的计算流程与位移不确定模型的区别在于因子个数不同，扬压力不确定模型的自变量因子有4个，分别为u(水位)、v(温度)、t(日期)、p(降雨)，因变量为w (扬压力)，它们分别构成4个样本数据信息对(u，w)，(v，w)，(t，w)，(p，w)。然后形成4个信息分配矩阵，进而可求得4个一级权重矩阵，再根据4个权重矩阵求得4个一级近似推理的结果，，将它们分别表示为行元素构成的综合关系矩阵R2，最后求得综合近似推理结果B2，最终经过信息集中处理，得到扬压力拟合值。

1.2.3 渗流量不确定模型

渗流量不确定模型的自变量也可取4个，分别为日期、水位、温度和降雨。与扬压力不确定模型的区别在于自变量相同，因变量不同。它们自变量同为日期、水位、温度和降雨，因变量前者为渗流量，后者为扬压力。它们的具体计算过程与扬压力不确定模型类似。

2 拟定监控指标

拟定安全监控指标的主要任务是根据大坝和地基抵御已经经历的荷载的能力，来估计和预测其抵御可能发生的未知荷载的能力，从而确定在该荷载组合下，大坝监控效应量的警戒值。现阶段监控指标包括变形、应力、扬压力、渗流量等。

2.1 置信区间法

置信区间法在业界被普遍采用，它的基本原理是统计理论中的小概率事件。如果取显著性水平为σ(一般为1% ～5%)，失效概率为px，则pα= α 为小概率事件，在统计学中认为是不可能事件;如果发生，则认为异常。它的基本思路是根据以往的监测资料，建立监测效应量与荷载之间的数学模型(如统计模型)。用这些模型计算各种荷载作用下监测效应量的拟合值与实测值E 之间的差值，这里我们可假设服从均值的正态分布，则有1 － α 的概率落在置信带(△= ± iδ)内，而且测值过程无明显趋势性变化，则认为大坝运行正常，反之则异常。

2.2 典型小概率法

该方法定性联系了强度和稳定的不利荷载组合所产生的效应量，并根据以往观测资料来估计监控指标，比置信区间估计法的精度提高了一步。在实测资料中，选择不利荷载组合时的监测效应量(Xmi)(例如大坝的水平位移)，则Xmi为随机变量，由观测资料系列可得到一个子样数为n 的样本空间:

其统计量可用下列两式估计其统计特征值:

然后，用统计检验方法(如A －D 法、K －S 法)，对其进行分布检验，确定其概率密度f(x)的分布函数F(x)(如正态分布、对数正态分布以及极值I 型分布等)。

令Xm为监测效应量的极值，若当X ＞Xm时，大坝将要出现异常或险情，其概率为:

求出Xm的分布后，估计Xm的主要问题是确定失事概率pα(以下简称α)，其值根据大坝的重要性而定，重要性高的工程，其值越小。在假设检验中该值被称为统计假设检验的显著性水平，其值越小则此假设检验的显著性水平越高。确定α 后，由Xm的分布函数直接求出。

3 诊断方法

3.1 模型诊断

3.1.1 统计模型诊断

根据建立的相应效应量模型并确定相应的系数和模型剩余标准差σ 之后，就可以求出时刻t 的计算值，如果选取显著性水平α = 5% ，则对应的效应量监控指标为，同理，如果选取显著性水平α = 1% 时，则对应的效应量监控指标变为。如果选取α =5% ，通过计算与该时刻实测值E(t)差的绝对值E(t)| ，并与相应模型的剩余标准差σ 的整倍数进行比较，根据概率统计理论，的概率为95.5%，的概率为99.7%，因此，可以认为在正常状态下不会发生|－E(t)＞3S| ，如果发生可以认为效应量状态出现了异常。由此，可以得到效应量的判定依据:①若|≤2S，则测值正常，大坝效应量处于正常状态;②若，则应跟踪监测2 ～3 次，如果效应量测值系列没有趋势性变化则效应量状态为正常;否则，效应量状态为异常，需进行成因分析;③若|，则测值异常，应该结合坝体自身情况和周围环境量变化情况进行综合分析，包括监测系统和大坝的工作状况。

3.1.2 不确定模型诊断

通过历史实测资料，可以建立不确定性信息模型，计算得到模型剩余标准差σ。实际诊断时，根据运行环境荷载，通过不确定性信息模型可以获得监测效应量的预测值，并计算监测效应量预测值与实测值的差的绝对值，通过绝对值与一定倍数的σ(如βσ)进行比较，诊断监测效应量的监控状态。根据不同级别，β 可以取1、2、3 等值，具体诊断方法与统计模型诊断方法相同。

3.2 监控指标诊断

根据大坝的重要性，确定失事概率Pα后，即可由概率分布函数F(Emi)直接求出监测效应量的安全监控指标。α 为与确定失事概率Pα相对应的显著性水平。然后将实际监测到的大坝监测效应量E 与安全监控指标Em进行对比:

1)若E ≤Em，则测值正常，大坝工作处于正常状态。

2)若E ≥Em，大坝工作状态为异常，需进一步分析，查找原因，及时采取措施。

4 预警方法

4.1 监控指标预警

根据监控指标诊断结果，判断位移、扬压力、渗流量和绕坝渗流是否超限(即超过拟定的监控指标值Em)，超限则报警。如果遇到效应量测值方向不同，例如大坝位移，则向下游位移测值、向上游位移测值应分别与相应的位移安全监控指标进行对比诊断，超限则报警。

4.2 设计限值预警

设计限值预警方案主要针对坝基扬压力测值的监控，它既可以采用置信区间法和小概率法作为扬压力是否超限的控制指标，还可根据设计扬压力折减系数或设计扬压力测孔水位作为诊断标准。同时水位工况、扬压力测孔位置应与设计水位工况、设计扬压力图形折减位置相对应，这样才有可比性，因此，实测扬压力折减系数计算时间应选用高水位时段，如接近正常蓄水位及以上水位时段。当实测扬压力折减系数α 不超过设计值或实测扬压力测孔水位不超过设计扬压力测孔水位时，则相应区域坝基防渗排水体系工作正常，否则异常，应进行报警，并加强监测和及时分析原因。

4.3 历史极值预警

通过对比混凝土重力坝各监测项目测点的历年特征值，判断实测值是否超过极值，超过说明本次测值超过往年正常水平，应进行报警。

需要指出的是，用来进行预警判别的特征值一般为最大值和最小值，因为平均值不能反映测值的上下浮动范围，故不作为评判标准。一般测值的最小值超过了历史最小极值则预警，同理超过历史最大极值也要预警，同诊断部分，历史极值因其可靠性不高，故作为一种辅助预警手段，用户可以在预警设置中，选择是否提供历史极值预警功能。

另外，专家经验预警也可以作为一种预警手段，原理就是建立专家数据库，按照监测项目和监测部位，将所有测点的测值上下限写入固定的数据库表，如果选择专家经验预警功能，则采集系统采集到的测点实测值可与数据库中相应测点专家经验数据表进行对比，超过则预警。

5 小 结

模型和监控指标作为最常用的大坝监测数据分析方法，已经被广泛应用，但目前的大部分大坝安全监测分析系统主要应用他们来进行单测点的数据拟合和预测，以及单测点的数据量程判断，并没有纳入到系统的大坝健康诊断和预警中去。但长远来看，水利工程将来主要的发展方向为安全监控和结构老化分析，对于重力坝监测，健康诊断和预警势必会成为重要组成部分，它们既可以提高工作效率，也可以为大坝安全提供保障。

［1］李占超．大坝安全监控指标理论及方法分析［J］． 水力发电，2010(05):64 －67.