2013年全国中学物理竞赛（预赛）第7题的多种解法

陈玉奇

（江苏省姜堰中等专业学校 江苏 泰州 225500）

题目：如图1，质量为m1的小滑块，沿一倾角为θ的光滑斜面滑下，斜面质量为m2，置于光滑的水平桌面上.设重力加速度为g，斜面在水平桌面上运动的加速度大小为______.

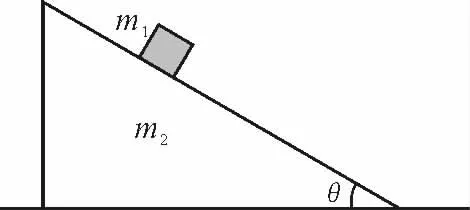
图1

这是一道经典的动力学问题，该类题型在近几年的高校自主招生和一些地区的物理竞赛中经常出现.由于本题涉及的已知条件较少，对学生来讲，如果不能找到合适有效的方法，要想快速而准确地求解具有一定的难度.其实本题的解法很多，既可直接应用牛顿第二定律列方程求解，也可以从非惯性系、数形结合、功能关系等方面进行突破，下面给出本题的几种分析方法.

解法一：用牛顿第二定律求解

由于要求加速度，很容易想到最直接的方法：牛顿第二定律，即从受力分析的角度出发进行求解.

方法1：m1和m2的受力情况如图2（a）所示，设m2相对于地面的加速度为a2，方向水平向左，m1相对于m2的加速度为a相，方向沿斜面向下，则m1相对于地面的加速度a1为a1＝a相＋a2，其矢量关系如图2（b）所示，a1在水平和竖直方向的分量为

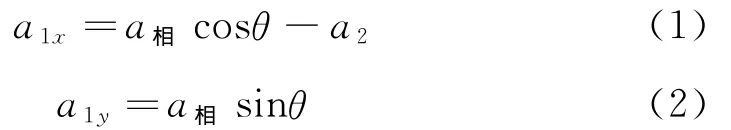
图2

根据牛顿第二定律，对m1和m2有

将式（1）和式（2）分别代入式（3）和式（4）中，可解得

由（6）、（7）两式可得

注意到N1＝N1′，将式（8）代入式（5）中，求出m2的加速度a2为

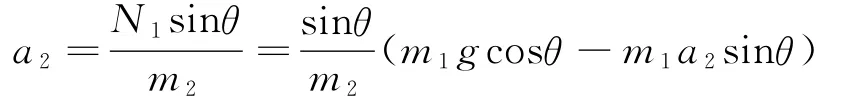
整理后可得

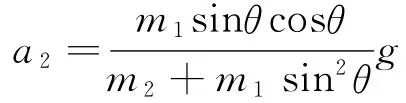
方法2：由方法1中的式（3）和式（4）消去N1，整理后可求得

对m1和m2整体应用系统的牛顿第二定律，因系统水平方向无外力作用，故系统水平方向上有

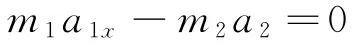
即

在水平方向上，由于m1和m2的加速度方向相反，则m1在水平方向上相对于m2的加速度大小为ax相＝a1x＋a2，而m2在竖直方向上无加速度，故m1在竖直方向上相对于m2的加速度为ay相＝a1y，由题中可知m1相对于m2的加速度方向沿斜面向下，故有

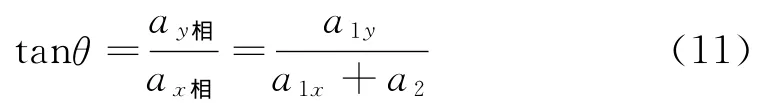
将式（9）和式（10）代入式（11）中，整理后可得

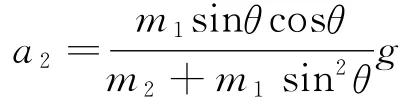
点评：牛顿第二定律应是解决动力学问题最基本的方法，其解题关键是正确作出物体的受力情况，在所研究的方向上建立牛顿第二定律方程.

如果对有相互作用的物体系应用牛顿第二定律，可以采取以下两种方法：第一是隔离法，正确作出被隔离物体的受力情况，理清单个物体间彼此力的关系、速度及加速度的联系，建立必要的辅助方程，才能正确求解.当然随着物体个数及受力分析的增加，其方程的个数以及求解过程的运算量也会随之加大，这就需要学生有较强的数学分析和运算能力.第二是整体法，即系统的牛顿第二定律，可以列成x方向和y方向的两个方程

在不涉及内力的计算时可使分析过程变得简便.但

是两种方法并不是彼此孤立，很多情况下联合使用，可以起到相互补充、相辅相成的作用.

解法二：用非惯性系求解

以斜面m2为参考系，由于斜面在水平方向有向左的加速度，所以该参考系为非惯性系.在非惯性系中，滑块m1的受力情况如图3所示，其中F是惯性力，方向与a2相反，大小为m1a2.

图3

对滑块m1，在垂直于斜面方向上有

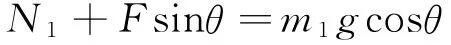
而对斜面m2，在其水平方向上仍有

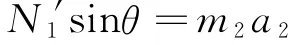
联立两式和N1＝N1′，解得斜面m2在水平方向运动的加速度为

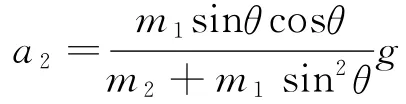
点评：我们平常研究问题所采用的参考系为惯性系，而相对于惯性系加速或转动的参考系，我们称为非惯性系.在非惯性系中，物体的运动不再遵从牛顿运动定律，如果通过转换参考系的方法来求解，解题过程会很复杂.但若引入惯性力的概念，就可以在非惯性系中应用牛顿运动定律的形式来解决相关的动力学问题.

需要指出，在相对于惯性系做加速直线运动的非惯性系中，惯性力为F＝－ma，a是非惯性系相对于惯性系的加速度，F是物体在非惯性系中受到的假想的力，实际上并不存在惯性力的施力物体.

如果非惯性系相对于惯性系转动，其惯性力大小为F＝mω2r，ω是非惯性系相对于惯性系的角速度，此惯性力称为惯性离心力.

引入非惯性系后，一般都能使分析和运算过程简化，是解决动力学问题的一个非常有效的方法.

解法三：用数形结合求解

方法1：设任一时刻t，m1和m2的位置关系如图4所示，AB即为m1在这段时间内的位移，与斜面间的夹角为α，其中Δx1和Δx2分别为m1和m2在这段时间内对应的水平位移大小.

在图4中，有DE＝BC，从而可得Δx2sinθ＝ABsinα，两边对时间求二阶导数，可知m1和m2实际加速度大小满足

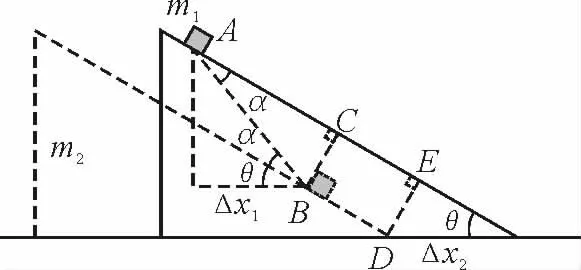
图4

作出m1的受力分析图，如图5，在力矢三角形中，由正弦定理，有

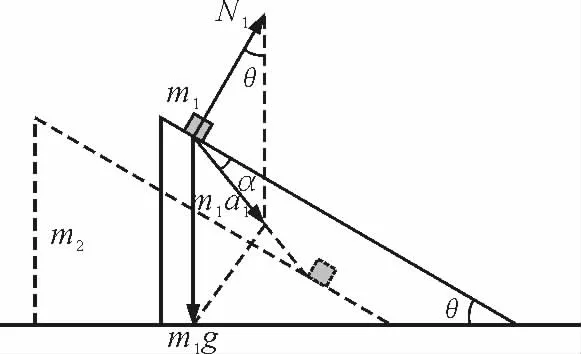
图5

从而

由于m1和m2在水平方向上无外力作用，水平方向动量守恒，有

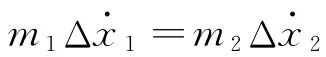
将此式对时间求一阶导数，有

即

由式（12）和式（13）有

由式（13）和式（14）有

即

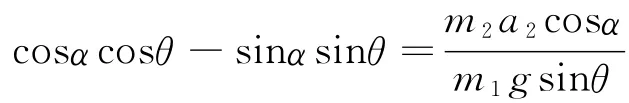
所以

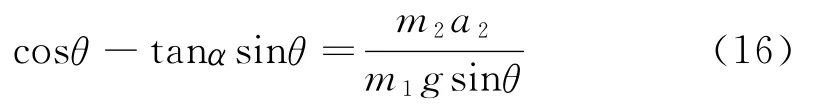
将式（15）代入式（16），整理后可得m2的加速度为

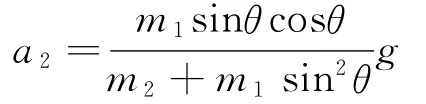
方法2：作出斜面静止和运动两种情况下的受力分析图，并将各个加速度之间的关系在图中一并画出，如图6所示.

图6

易知AB就是斜面运动时m1受到的合力，而无论斜面是否运动，斜面对m1的弹力均垂直于斜面，故斜面静止时，斜面对m1的弹力与重力m1g的合力就是AC的长度，且此合力大小为m1gsinθ，所以在图6所示的加速度矢量三角形ABD中，AC段对应的加速度大小应为gsinθ，由该加速度矢量三角形中的几何关系可得

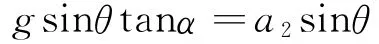
即

如果能求出tanα的值，代入上式即可求得a2.

因m1做匀加速直线运动，为方便计算tanα，可以假设m1从斜面的顶端滑至斜面底端，如图7，在此过程中，m1的水平位移大小为x1，斜面的位移大小为x2，根据水平方向动量守恒，有m1x1＝m2x2.

图7

由图7中几何关系可得

由以上两式求得

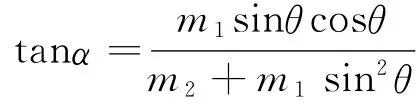
代入a2＝gtanα，从而求得斜面在水平方向上的加速度为

点评：使用本解法求解时，关键要理清物体间诸如受力情况、位移大小和方向之间的联系，正确找出几何图形间的等量关系，如加速度a1和a2既与位移对时间的二阶导数有关，又在物体的受力情况中有所体现，而以上这些物理量分别与位移图形、力矢三角形相对应，只要正确找出连接它们之间关系的桥梁，运用合适的数学方法，问题就可迎刃而解.

解法四：用连接体的关联速度和加速度求解

沿斜面方向和垂直于斜面方向上建立xOy坐标系，m1和m2的实际加速度a1和a2如图8所示.

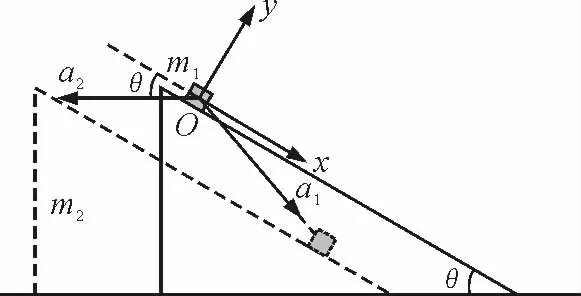
图8

因为m1和m2始终接触未发生分离，故二者在垂直于斜面方向上无相对运动，二者的实际加速度在垂直于斜面方向上的分量相同，即

且

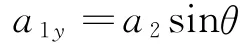
由前面对两物体的受力分析可知，对于m1，在垂直于斜面方向上有

对m2，在其实际加速度a2方向上有

联立各式，并注意到N1′＝N1，可以很方便地解出

点评：所谓关联速度和加速度，就是通过某种方式联系起来的速度、加速度，比如两个物体在张紧的轻绳两端运动，这时两个物体的速度、加速度就是通过不可伸长的轻绳发生联系，故有“沿着绳子方向上的速度、加速度一定相等”这个等量关系.

在本题中，m1和m2均不可发生形变，由刚体的力学性质及“始终接触未分离”这个约束可知，沿接触面的法线方向，接触双方必须具有相同的法向分速度和加速度，否则两物体将分离或发生形变.

所以，本解法的关键点就是m1和m2在垂直于斜面方向上的加速度大小相等，对二者列隔离方程时，务必在这个方向上进行突破.

解法五：利用导数求解

建立如图9所示的坐标轴Ox，向右为正方向，设在任一时刻t，m2在Ox轴中的坐标为x2，m1相对于m2的位移为s，则m1和m2在水平方向的速度及m1相对于m2斜面的速度分别为s·cosθ＋x·2，x·2和s·，方向如图9所示.（这里的速度均为矢量形式，当然也可以列标量式，取其大小代入计算，只需将x·2反向即可）

图9

m1和m2组成的系统在水平方向动量守恒，有

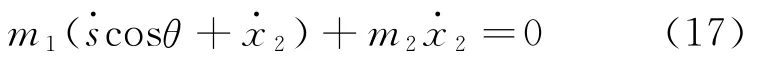
在m1由静止沿斜面下滑位移为s的过程中，根据动能定理，有

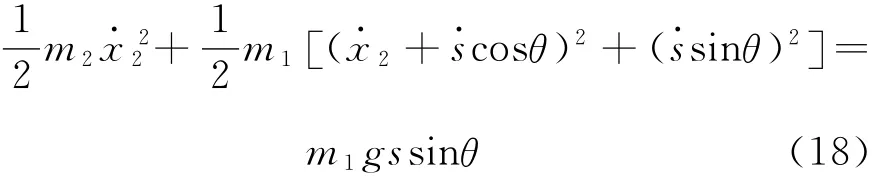
由式（17）可得

将式（19）代入式（18），整理后，有

上面等式两边对时间求导，得

所以

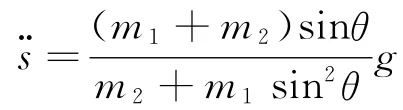
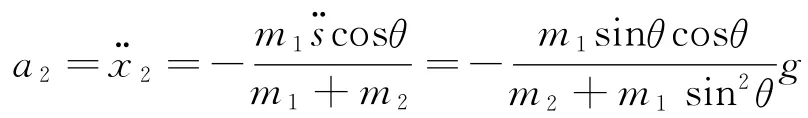
负号表示加速度方向向左.

点评：导数和微分知识已经作为高中数学教学内容的一部分，而高中物理教学大纲中也明确指出，“应用数学工具解决物理问题的能力”是物理教学的一项重要内容，也是物理竞赛和高考能力考查的重要组成部分，可以加强学科之间的相互渗透，更能培养学生科学的思维方法，提高学生分析问题和解决问题的能力.

用导数知识求解物理问题时，应理解某一物理量的导数与另一物理量的对应关系，包括大小和方向，如加速度是速度的变化率，也是位移对时间的二阶导数，即

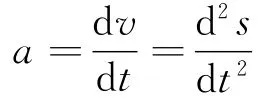
电流是通过导体横截面的电荷量对时间的一阶导数，即

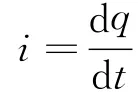
学生对于高考和竞赛真题具有强烈的研究兴趣，如果我们能对该题的几种解法进行详细的剖析，引导学生从多途径、多角度地去分析问题，不仅可以帮助学生总结解题规律，达到对知识的融会贯通，而且可以提高学生的逻辑思维和发散思维能力.