假如给平行板电容器两板充以不等的电荷量

张延赐 王金聚

（浙江省温州中学 浙江 温州 325000）

在学习了平行板电容器后，学生往往会提出这样的问题：如果给两个平行板充以不等的电荷量，两板之间还是匀强电场吗？

让我们归结于如下一道例题.

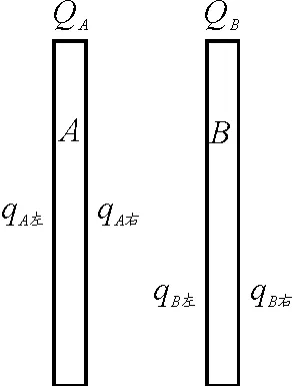
图1

【例1】两块形状、大小都相同的金属薄板A和B，如图1所示，两个板间距远小于板面的线度.现使两板分别充以电荷量QA，QB，当静电平衡后，4个板面上的电荷量qA左，qA右，qB左，qB右分别是多少？

解析：此题看似无从下手，实际上只要想想静电平衡时导体内部的场强处处为零这一结论，就不难找到解决问题的突破口.

两薄板共有4个大的平面，每个平面都可看作是一个无限大的均匀带电平面，它们在A，B内部都会产生各自的场强，但其合场强为零.如图2所示，我们在QA，QB的正负未知的情况下，不妨先把qA左，qA右，qB左，qB右都理解成正电荷，则对A板内部的任一点而言，qA左在该点产生的场强向右，而qA右，qB左，qB右在该点产生的场强则向左，由该点的合场强为零可得

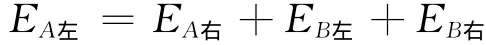
同理，对B板内部的任一点而言，同样有

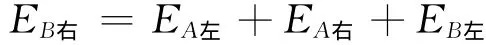
由于无限大均匀带电板在空间某处的场强与板上电荷的面密度成正比，所以有

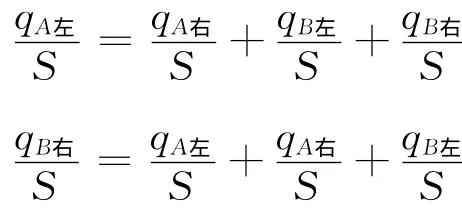
结合关系式

可以解得

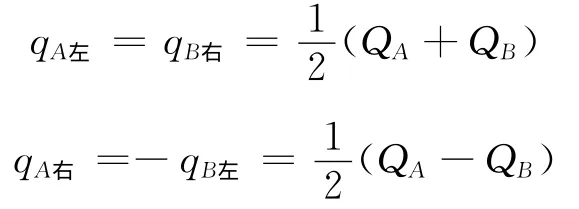
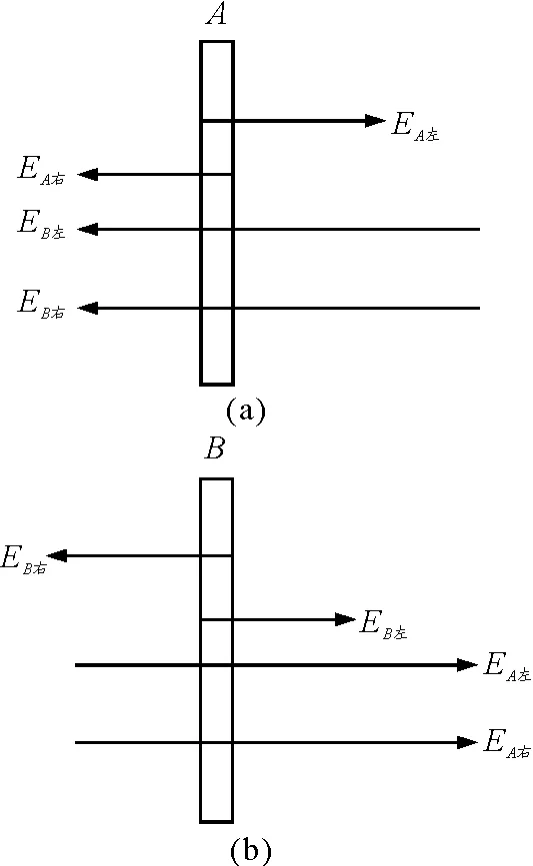
图2

从上述结果可以看出，不论QA，QB的正负如何，两板相距最远的两个平面所带的电荷量、电性都完全相同，而相距最近的两个平面所带的一定是等量异号电荷.也就是说，两板之间的电场仍然是匀强电场，公式Q＝CU，U＝Ed仍然适用.

【例2】平行板电容器的电容为0.2μF，给两板分别充以Q1＝＋6×10－6C，Q2＝－2×10－6C的电荷量，求两板之间的电势差.

解法1：由上述公式可知，最近的两个板面所带的电荷量为

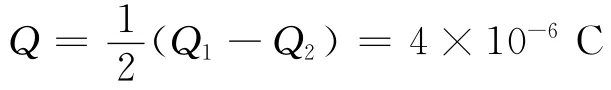
所以两板之间的电势差为

实际上，除了利用上述推出的现成结论求解外，还可以采用其他的求解方式.方法如下.

解法2：配平法.

设想我们对两板分别再充以两个完全相同的电荷量ΔQ，并且使得充电后两板变成等量异号的电荷＋Q，－Q，则充电后两个板之间的电势差可用公式U＝算出.考虑到两板所充的两个完全相同的电荷量ΔQ并不能产生多余的电势差，所以U就是两板间的最终电势差.即

联立解得

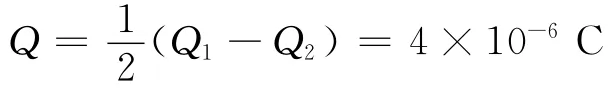
所以两板之间的电势差为

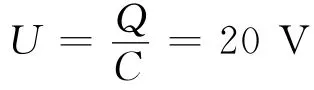
解法3：转移电荷量法.

假如电容器的两个极板分别带有电荷＋Q和－Q，设想我们把正极板的电荷量＋Q转移到负极板，则两极板的电势将变得相等.所以对于公式Q＝CU，我们也可以这样来理解：Q就是要使两个板的电势变为相同而需要从一板向另一板转移的电荷量.

设两个极板分别带有电荷Q1和Q2，要使两个极板的电势相同，就要使两板的带电荷量及电性都相同，这就需要从一板向另一板适量地转移一些电荷量，则需要转移的电荷量为

所以两板之间的电势差为

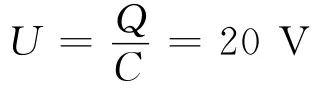
从上面的分析可以看出，虽然平行板电容器两个极板的带电荷量不等，但当达到静电平衡后，对于最近的两个带电平面而言，仍然带有等量异号电荷，它们之间的电场仍然是匀强电场，公式Q＝CU，U＝Ed仍然适用.