城市土地价格的空间插值估计方法

张 宇，刘 春

城市土地价格的空间插值估计方法

*张 宇，刘 春

（同济大学测绘与地理信息学院，上海 200092）

随着城市的快速发展，准确的衡量城市土地价格，以及土地价格分布，对于城市建设规划具有非常重要的作用。首先，获取土地价格的实际数据，并对数据的空间特征和统计学特征进行分析。然后，在空间统计分析的基础上，设计出对克里金插值的半变异函数进行拟合的实验方案，并从中选出误差最小的估计模型。最后，得到土地价格估计模型后，以某城市为例进行土地价格估计，并对估计结果进行误差分析。分析结果与预测结果基本一致，估计得到的土地价格分布也与实际情况相符，准确的估计结果在所有结果中占90%以上，得到较好的估计精度。

地统计分析；半变异函数；克里金插值；误差分析；土地价格估计

随着经济的快速发展，城市逐渐向经济全球化、交通网络化、调控宏观化方向发展。十二五期间，信息化都市的理念将成为城市发展的又一次飞跃。2011年开始，许多城市开展的大规模土地价格调查，目的是让国土部门通过土地价格的历史数据对城市土地等级重新进行评定。土地的等级划分对于土地的利用、规划和管理都具有重要的作用。因此，城市土地管理部门迫切需要一种能够正确反映土地价格分布规律的方法来帮助他们完成城市规划中的重要工作。

利用空间插值对土地价格进行估计是分析土地价格分布规律最常用也是最有效的方法，利用地统计学的方法对土地价格数据的空间分布特性进行分析是共同的方法。王霞等[1]利用剔除土地价格在空间中形成的二次函数的趋势，可以得到城市内部地价变化的区域规律和空间分布格局；曾怀恩等[2]利用遗传算法为基础对估计结果进行迭代计算，使估计误差逐渐减小，直到满足估计要求为止；此外，也可以通过研究空间数据之间的相关性，判断数据之间的关系，再根据数据间的关系推算出数据与空间的关系，从而得到数据的空间分布特征[3]；郑光辉等[4]利用克里金插值法对样点地价进行空间插值，根据空间插值的统计结果得到土地价格的频率直方图，再通过频率直方图，按一定的标准对土地价格进行级别划分，利用全市的土地级别划分结果，可以对土地开发和利用提供有效的帮助；然而不同的插值方法会得到不同的估计结果，通过对不同插值方法结果的对比，可以得到针对某一数据的最佳估值，这个最佳结果可以作为最终估计进行土地评估和规划[5]。

事实上，缺少对实际数据和估计结果的误差分析，并不能保证估计结果的准确性。而根据数据的分布特征和统计学特征对数据进行变换或处理，可以得到更精确的空间插值结果。本文通过分析数据的分布特征设计合理的模型估计方案，然后根据估计方案对模型的系数进行拟合，通过误差分析得到精度最高的估计模型，最后利用实际的数据对模型进行检验，可以得到更合适的估计结果。

2 城市土地价格的分析和估计

城市土地价格估计分析主要包括空间插值方法选择、数据分析、半变异函数估计、土地价格估计和结果分析等几个基本步骤。本文处理的主要流程如图1所示。

土地价格估计的主要方法是空间插值，空间插值方法与数据的空间特征有紧密的联系。因此，首先根据数据的特征选择合适的插值方法，再进行空间插值模型系数估计。分析数据特征有三方面内容：分布特征分析、趋势分析和相关性分析[3]。分析结果用于估计方法的确定，确定后可以进行模型估计，再利用模型估计出全市范围内的土地价格。最后利用实际数据对估计结果进行检验，通过误差分析确定出最佳估计模型。

图1 城市土地价格估计和分析流程

3 城市土地价格的空间插值模型

土地价格估计模型确定的基本流程中，最重要的是半变异函数的系数估计，而半变异函数与克里金插值模型参数的确定具有直接的关系。为此，需要确定插值模型的具体参数以确保土地价格的空间内插估计。

3.1 空间插值方法选择

土地价格估计使用的空间插值方法主要有克里金插值法、样条函数插值法和反距离权函数（IDW）插值法。克里金插值法以空间统计学作为基础，可以得到内插过程中的误差，而且对于密度较小、分布不均匀的数据，使用克里金插值法有一定的优势。样条函数法要求数据分布是比较平滑的表面，并且对密度较大的数据求等值线有较好的精度；IDW法适用于对数量较多、分布均匀的点进行插值[3]。由于城市结构的区域性，使得土地价格数据分布并不均匀，而且土地用途、开发程度各不相同，数据在某一区域比较密集而在另一区域则比较稀疏。这种密度不大、分布不均匀的数据，更符合克里金插值方法。

克里金插值方法以统计学理论为基础，利用半变异函数计算数据点之间的空间关系。半变异函数以区域化变量理论为基础，通过对变异函数的计算以及变异曲线的分析，判断数据的变异特征和变异类型[5]。同时，半变异函数还可以得到较准确的精度。

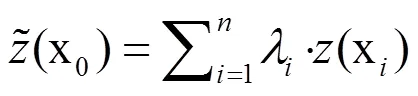
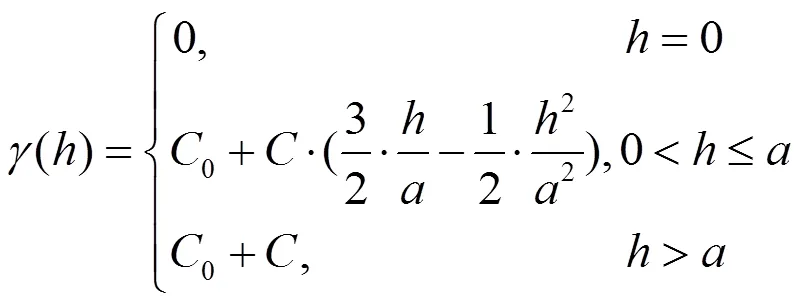
3.2 模型估计数据预分析

确定出空间插值方法及半变异函数模型后，需要对半变异函数的系数进行估计，而系数的确定与数据的分布特征和统计学特征有着密切的关系，因此，分布特征分析、趋势分析和相关性分析这些数据特征的分析方法便可以用于估计系数的确定。土地类型从用途分可将城市土地分为住宅用地、商业用地和工业用地以及综合用地四类，考虑到住宅用地与城市居民的关系最为密切，因此，本文选择了住宅用地的土地价格数据作为实验数据。

3.2.1 分布特性分析

数据的空间分布特性对空间插值方法的选择和估计模型的预测均有重要作用，从图2(a)可以看出住宅用土地价格分布特征是似于指数函数。对原始数据用对数法和Box-Cox法进行正态变换，以观察插值结果的精度变化。经过试验，系数为0.06的Box-Cox方法得到的变换效果更好。变换前后的分布情况如图2所示。变换后图像趋近于正太分布，有利于对数据结构进行进一步分析。Box-Cox变换如公式(4)

()为位置上的原始数值，为变换后的值。为系数。当等于1/2时，为平方根变换；当等于0时，为对数变换[7]。

(a)

(b)

3.2.2 趋势性分析

如果数据的分布在空间上与某种曲面相似，则可以利用数学公式对这样的分布进行表达。但是有时数据表面并不是数学公式拟合后的平滑表面，会有许多的起伏。想要研究这些起伏对数学模型的影响，就需要将数据中所包含的有规律的曲面(也称趋势面)去除，之后再对剔除趋势面的差值进行分析，便可以得到数据在空间分布中的微小变化规律[7]。本例中土地价格数据的空间分布特征是以市中心为最高点，向周围逐渐递减，在三维空间中形成一个具有最大值的二次曲面，因此可以用二次多项式来表示这种趋势。

3.2.3 自相关性分析

空间自相关理论认为：事物彼此之间距离越近则属性越相似[8]。因此，可以用半变异函数云图来分析数据点之间的关系，这种云图表达了半变异函数值与样点对之间距离的关系。半变异函数值表示样点对之间的差异大小，距离越近的点的土地价格应该越相近。因此，如果在小距离的范围内出现半变异函数值过大的情况，说明数据的分布不合理，或者数据受当地特殊条件影响有所变化，需要重新审核这些数据的准确性。

3.3 模型系数估计

确定了空间插值方法后，需要得到模型的最佳参数，克里金插值法的参数主要为半变异函数的系数，分别称为块金值、自相关阈值及基台值。估计半变异函数，首先要确定一个合适的步长大小。为了减少无关的数据在计算中可能的合并运算而将数据点对分成不同的距离级，该距离级的大小就是步长，这种方法称为步氏分组[4]。步长的确定与实际使用的数据相关，因此利用不同的数据进行价格估计前均需要确定步长大小。通过计算，实验数据最合适步长为900 m，步长组数为12。给出步长大小后，便可以利用实验数据估计出半变异函数。

通过对数据进行预分析，可以得出五种变换方案，这些方案用于对半变异函数的系数进行估计。第一种方法利用地统计分析模块的缺省值进行估计，也就是不采用数据转换和趋势剔除；第二种方法对数据进行转换，根据前文所得到的结果，使数据最接近正态分布的转换方法为Box-Cox，参数为0.06；第三种方法使用趋势剔除，根据前文得到的结果，采用二次多项式进行剔除；第四种方法则是将第二、三种方法联合起来，同时进行数据转换和趋势剔除；第五种方法是将Box-Cox的参数进行修正后再与第三种方法联合起来。对比分析这五种方案的估计误差，其中误差最小的结果便是最佳模型的估计方案。五种方案的误差结果如表1：

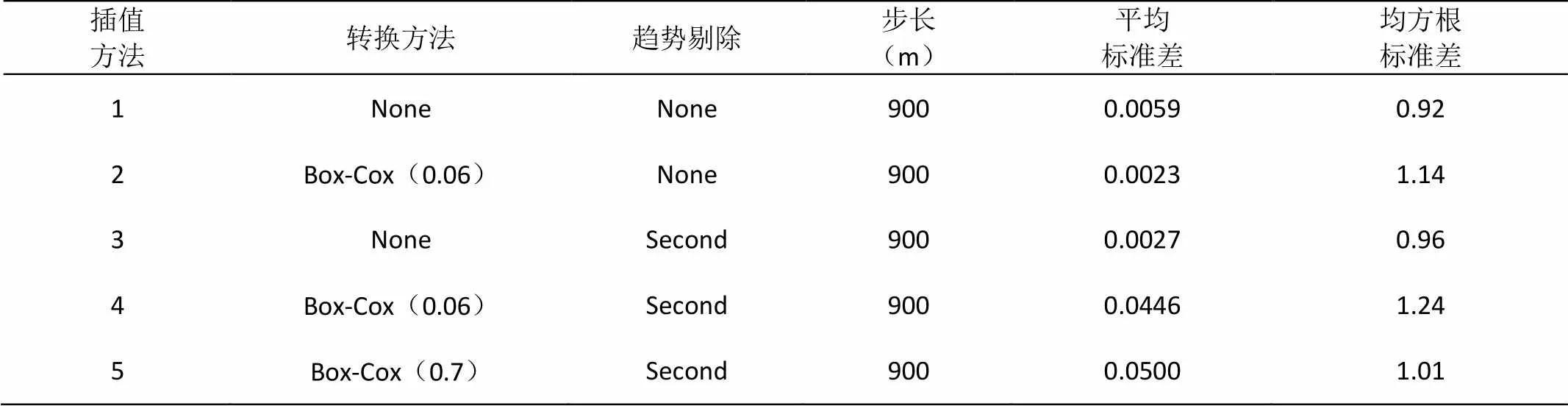
表1 半变异函数误差对比分析

对于一个预测模型的精确性，其平均标准差接近于0，均方根标准差接近于1，则预测结果的精确性越高。从表1中可以看到，Box-Cox转换方法对于平均标准差的精度有较好的提高，但均方根标准差则相差较大；二次多项式趋势剔除方法较好的提高了预测模型的精度；第四种方法产生了较大的误差结果分析原因是由于趋势剔除后数据的分布方式发生了一定的变化，导致原来的变换形式无法使数据达到较好的正态性，因此需要对Box-Cox变换方法进行修正。从表1中可以看出，第2种方法平均标准差最小，均方根标准差处于中等水平，考虑到平均标准差是衡量误差大小的直接数据，收到误差传播的影响较小，因此选择这种方法得到的结果作为半变异函数的最佳系数，选择的变换方法为Box-Cox，系数为0.06。

3.4 模型检验

根据上文的分析，最终采用第3种方法得到预测模型为最佳估计值。由这种方法得到的估计参数为：块金值23196，偏基台值为118690，阈值为4881.72，步长900，半变异函数模型为球状模型。最终得到半变异函数的估计模型为：

4 实例分析

4.1 数据分析

实例数据源自于某市国土局在2011年开展全市土地管理规划工作过程中采集的土地价格数据。数据的主要属性有土地价格、交易类型、交易时间、影响因素等。土地价格数据来源于国土部门，因此数据是真实可靠的。根据土地用途，土地数据主要分为住宅用地、商业用地、工业用地等。不同类型的土地在使用方式上有一定的区别，因此价格分布也会有所差别[9]。本文以住宅用地为例，利用估计模型对土地价格进行空间插值，再将结果与实际价格进行对比，通过误差分析，确定估计模型的准确性。住宅用地数据点的分布如图3。

图3 数据点的分布

4.2 土地价格模型内插

对住宅用地的土地价格进行数据变换和去趋势分析，可以得到数据的分布特征，并根据分布特征对数据进行变换；然后，利用变换后的数据计算出克里金插值的半变异函数的估计系数；接着，针对数据分布体现出的不同特征对数据做相应的变换，得到不同的半变异函数估计结果；最后，将每种估计结果相互对比，再利用误差检验的方法确定最有效的估计结果。然后利用克里金插值法进行空间插值，得到最佳模型的空间插值结果，如图4：

图4 估计模型空间插值图

从图中可以看出，土地价格估计结果以市中心——江东和海曙区为最高，从市中心往外，距离市中心越远价格相对越低。而镇海区中部的土地价格比东西部的地价要低，这是由于与这一区域多为山区、人烟稀少，土地价格较低。另外，北仑区西部形成一个次级中心，也与实际情况相符。综合来看，用估计模型得到的土地价格分布与实际土地价格分布基本相符。

4.3 结果验证和分析

利用空间插值可以得到对地价样点的估计价格。检验数据主要由政府相关部门以及土地信息公司提供，因此数据的准确性较高，实测数据主要以城区土地价格为主，在乡村地区的土地价格数据比较稀少，因此估计精度在主要市区较高，而在乡村或山区会有所下降。今年来，土地价格不断变化，这种变化影响了估计结果的精度。使用相对误差计算则可以减小估计误差。

根据上文的分析，本文采用相对误差的方法对土地估值的精度进行计算。计算方法为：

估计误差的统计结果如表2。计算出结果后，绘制出相对误差的平率直方图，结果显示服从正态分布N(0.7，2.252)，如图5。

表2 土地估计误差统计结果

图5 土地价格估计相对误差频率直方图

由于本例的土地估计范围涉及到全市范围的土地，并且只涉及到住宅用地的土地价格，因此估计的精度与理想值略有差距。经统计，在一倍中误差范围内的数据占全部数据的77.3%；两倍中误差范围内的数据占93.4%。设两倍中误差为极限误差，则估计结果满足要求，因此可以认为估计模型对土地价格估计的结果比较好，可以用于同一类型土地价格的估计。

5 结论

本文对土地价格数据的分布情况进行了分析，根据半变异函数的特征将数据的空间分布与统计学分布相结合，确立了模型估计的思路。同时利用误差分析的方法在几种模型估计方案中选择出估计误差最小的方案，从而得到了住宅用地土地价格的最佳估计模型。通过上文的分析，可以得到以下结论：

(1)城市土地价格数据密度比较小、空间分布不均匀，这些特征更适合使用克里金插值方法。

(2)本文采用了五种方法对半变异函数的系数进行估计，并通过误差检验得到五种方法估计结果的精度以及数据分布情况。最终得到经过Box-Cox变换处理后的估计结果最佳。

(3)估计结果与实测结果数据进行对比，设两倍中误差为极限误差，则93%的估计值满足要求，因此可以认为估计模型能有效的对土地价格进行估计，估计精度比较好。

[1] 王霞,朱道林.基于克里金插值方法和GIS技术的地价时空格局研究[J].重庆建筑大学学报,2007,29(1):101 -105 .

[2] 曾怀恩,黄声享.基于克里金方法的空间数据插值研究[J].测绘工程,2007,16(5):5-9.

[3] Johnston Kevin, VerHoef, Jay M, KrivoruchkoKonstantin. ArcGIS Geostatistical Analyst Tutorial [EB/OL].http:// webhelp.esri.com/arcgisdesktop/9.3/pdf/Geostatistical_Analyst_Tutorial.pdf.2011-12-15.

[4] 郑光辉,黄克龙,张志宏,等. 运用克里金空间插值技术进行土地级别划分[J].南京师大学报,2007,30(1)：112-116.

[5] 刘光孟,汪云甲,张海荣.空间分析中几种插值方法的比较研究[J].地理信息世界,2011,9(3):41-45.

[6] 胡小荣.变异函数球状模型的拟合研究[J].本溪冶金高等专科学校学报,2000,2(4):41-43.

[7] 曹庭校,秦俊华. 半变异函数分析法的初步实践 [EB/OL].http://www.lunwenwang.me/kuangshangongchengjishu/kuangshandizhixue/15916.html.2007-6-15/2011-12-15.

[8] 陈思源,曲福. ESDA支持下的城市地价分布信息提取[C].2005年中国土地学会学术年会, 2005:142-147.

[9] 龚黎君.地统计学在沅江市城镇地价研究中的应用[D].长沙:湖南师范大学,2006.

[10] 徐成东,孔云峰,仝文伟.线性加权回归模型的高原山地区域降水空间插值研究[J].地球信息科学,2008, 10(1):15-19.

SPATIAL INTERPOLATION ESTIMATING METHOD OF URBAN LAND PRICE

*ZHANG Yu, LIU Chun

(College of Surveying and Geo-Informatics, Tongji University, Shanghai 200092, China)

With the rapid development of cities, it is very important for urban planning and city development that obtains accurate price of urban land and describes the distribution of that accurately. In this paper, the real data of land price has been got, and the spatial character and statistical character of it has been analyzed with the method of geostatistical analysis. Base on the result of geostatistical analysis, semi-variogram function of Kriging Interpolation has been designed to make an experiment to estimate the land price, and then the best estimation model is selected for the smallest error. With the best model, the real land price of a city is estimated as a study case, and the error is analyzed. The results of price estimation are similar to the prediction results. And the distribution character of land price that is got with the function estimated before conforms to the actual too. The analysis results have a little deviation with measured data, and to meet requirements, the exact results account for more than 90 percent, reflecting the good estimation accuracy.

geostatistical analysis；kriging interpolation；semi-variogram, error analysis，land prices estimating

F293.2

A

10.3969/j.issn.1674-8085.2014.03.002

1674-8085(2014)03-0007-06

2013-12-09；

2014-01-11

国家自然科学基金项目（41371333）

*张 宇(1988-)，男，内蒙古呼和浩特人，硕士生，主要从事数据挖掘和空间统计分析研究(E-mail: happyyu1988@126.com);

刘 春(1973-)，男，江苏南通人，教授，博导，主要从事机载和地面激光扫描数据处理理论与方法、滑坡灾害强化监测与模型研究、智能交通与主动交通安全GIS系统、传感器网络集成与应用研究(E-mail: liuchun@tongji.edu.cn).