基于群体早熟程度和非线性周期振荡策略的改进粒子群算法

朱喜华，李颖晖，李宁，范炳奎

（1. 空军工程大学 航空航天工程学院，陕西 西安 710038；2. 中国人民解放军95291部队装备部，湖南 衡阳 421002）

1 引言

粒子群优化算法（PSO）是进化算法的一个重要分支，最早由美国学者 Kennedy和 Eberhart于1995年提出，是一种基于种群迭代搜索的自适应优化算法，它通过种群粒子中个体的交互作用来寻找复杂问题空间中的优化解。与遗传算法等其他进化算法相比，粒子群优化算法具有结构简单、参数少及收敛速度快、容易实现等优点，具有较低的空间复杂度和时间复杂度，并被证明能够以较小的计算代价获得良好的优化解[1]，因此得到了广泛的研究和应用。随着通信技术的发展，通信领域也出现了各种优化问题，如通信星座优化设计[2]、无线传感器网络的感知器分布优化[3]及生存周期优化[4]等，要解决这些问题就需要采用先进的优化算法。因此，研究粒子群算法及其改进策略，并将其应用于通信领域的优化计算具有十分重要的理论及工程实际意义。

基本PSO算法具有快速收敛的特性，但存在寻优效率较低、容易停滞于局部最优值以及早熟收敛等问题[5]。早熟收敛是由于粒子群体的多样性在迭代搜索过程中快速丢失造成的，对此，很多学者提出了改进措施，主要采用以下2种策略。1)对粒子的速度和位置采用不同的参数策略来更新，如采用线性变化的动态惯性权重。该策略的主要特点是忠实于 PSO的原始思想，速度和位置的更新由粒子自身经验和群体经验作指导[6]。2)引入变异算子[7]。变异操作能够提高粒子群算法的开拓能力，并有效克服早熟收敛，但是选择对收敛性能有显著提升的变异算子十分困难。此外，如何变异、何时变异、变异概率以及变异位置等问题在实际操作过程中都难以确定。

本文在参考粒子群算法各种改进策略的基础上，提出了一种新的基于群体早熟收敛程度和非线性周期振荡参数策略的自适应混沌粒子群优化算法。该算法利用混沌的遍历性特点初始化粒子的速度和位置，使搜索空间遍布整个优化变量的取值空间；根据粒子群的早熟收敛程度和粒子的适应度值对不同粒子的惯性权重采用不同的自适应更新策略；在算法的整个搜索迭代过程中，粒子的个体学习因子和社会学习因子都周期性地非线性变化，模拟鸟群在觅食过程中不断分散和重组的现象。基准测试函数的仿真实验表明，本文提出的算法能有效平衡粒子群的局部搜索能力和全局搜索能力，避免群体早熟收敛并提高最优解质量，且具有良好的稳定性。

2 粒子群算法的基本原理

PSO算法的思想来源于鸟类迁徙觅食的模型，其关键在于每个粒子在解空间内根据自己的记忆和从其他粒子获取的社会信息更新自己的位置，通过个体间的协作与竞争，实现复杂空间中最优解的搜索，其数学描述为：每个粒子是D维搜索空间中的一个点，设粒子规模为N，第i个粒子的位置矢量可以表示为xi=(xi1,xi2,…,xiD)，速度矢量为vi=(vi1,vi2,…,viD)；pi=(pi1,pi2,…,piD)为第 i个粒子搜索到的最优位置，称为个体极值，表示粒子的个体经验；pg=(pg1,pg2,…,pgD)为整个粒子群体搜索到的最优位置，称为全局极值，表示粒子的群体经验。

对于第k+1次迭代，每个粒子按照式(1)更新自己的速度和位置。

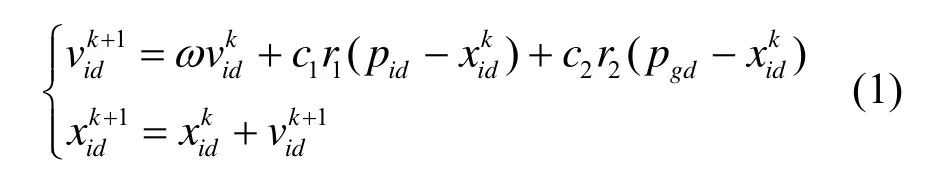
其中，i=1,2,…,N，N为粒子规模；d=1,2,…,D，D为解空间的维数，即自变量的个数；ω为惯性权重；c1为粒子的个体学习因子，c2为社会学习因子，分别用于调节粒子向个体极值和全局极值方向飞行的最大步长；r1、r2为[0,1]之间均匀分布的随机数。

3 粒子群算法的时变参数策略

惯性权重ω描述了粒子上一代速度对当前代速度的影响，控制其取值大小可调节PSO算法的全局与局部寻优能力。惯性权重值较大时，全局寻优能力强，局部寻优能力弱；反之，则局部寻优能力增强，而全局寻优能力减弱[8,9]。为此，学者对起初的固定权重策略提出了各种改进方案，典型的有线性递减策略、非线性递减策略和随机策略等。

线性递减策略的原理是：在不同的搜索阶段采用不同的惯性权重，在搜索初期采用较大的惯性权重有利于搜索整个空间，不易陷入局部最优值；在后期当算法收敛到较优解时，则倾向于进行局部挖掘，使粒子迅速收敛于全局最优值，其数学描述为[10]

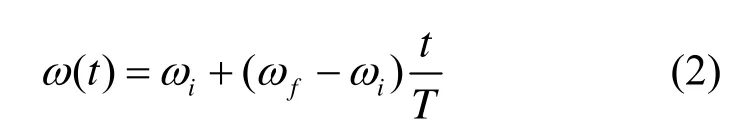
其中，iω、fω分别为惯性权重的初值和终值，t为当前迭代步数，T为最大迭代步数。

Eberhart和Shi经过研究发现线性递减策略对于动态系统的效果并不理想，进而提出了一种惯性权重随机变化的策略[10]

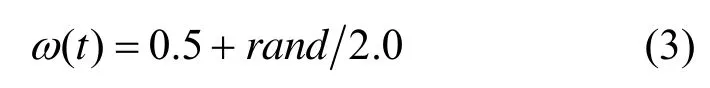
其中，rand为[0,1]之间均匀分布的随机数。

经验证，采用随机策略时早期阶段的收敛速度明显加快，但是，在多个测试函数中所表现出的收敛性能却并不理想。为此，有学者进一步提出了非线性递减策略，如式(4)所示[5]。

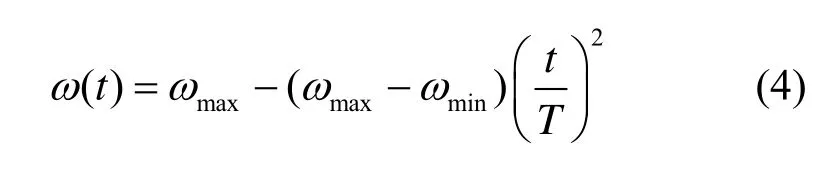
针对惯性权重进行改进研究的同时，学者Ratnaweera对学习因子进行了改进，指出了学习因子为常数的缺陷，并提出了类似于惯性权重线性变化的策略，如式(5)所示[10]。

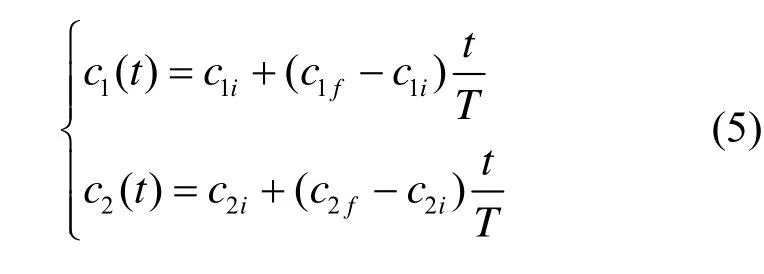
其中，c1i和 c1f是个体学习因子的初值和终值，c2i和c2f是社会学习因子的初值和终值。

4 基于群体早熟程度和非线性周期振荡策略的混沌改进方法

粒子群优化算法虽然具有算法结构简单、参数少及收敛速度快等优点，但容易陷入到局部极值点，导致得不到全局最优解，原因有两方面：一是待优化函数的性质，二是在运行过程中由于算法的参数设计、粒子规模选择不恰当等原因，导致在计算过程中粒子的多样性迅速消失，造成算法“早熟”。本文主要针对算法的参数设计进行改进，同时利用混沌特性初始化粒子群的参数，以尽可能提高算法的性能。

4.1 粒子参数的混沌初始化

混沌具有遍历性、随机性和规律性等特点，能在一定范围内按其自身规律不重复地遍历所有状态，使得混沌优化理论成为一个崭新的课题，得到了学者们的广泛重视和大量研究[11,12]。混沌优化是一种新颖的优化方法，它利用混沌系统特有的遍历性特点进行优化搜索，不要求目标函数具有连续和可微的性质，其基本思想是首先产生一组与优化变量相同数目的混沌变量，用类似载波的方式将混沌引入优化变量使其呈现混沌状态，同时把混沌运动的遍历范围放大到优化变量的取值范围，然后直接利用混沌变量进行搜索。

一般应用Logistic映射（逻辑映射）来产生混沌变量，其映射形式如下

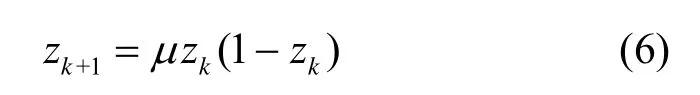
其中，μ∈[0,4]为控制变量，zk∈[0,1]，k=0,1,2,… 。当μ=4时，式(6)完全处于混沌状态，此时，轨道布满区间[0,1]，即混沌轨道在区间[0,1]内遍历。由任意初值z0∈[0,1]可迭代出一个确定的混沌时间序列z1,z2,z3,…。

4.2 基于群体早熟程度的自适应惯性权重调整

在PSO算法中，搜索陷入局部极值往往表现为微粒几乎停止不动。当群体的最优适应值长时间未发生变化（停滞）时，应根据群体早熟收敛程度自适应地调整惯性权重。如果对整个群体采用相同的自适应操作，则当群体已收敛到全局最优附近时，优秀粒子被破坏的概率会随着其惯性权重的增加而增加，从而使PSO算法的性能下降。为了充分发挥自适应操作的效能，本文提出了一种根据群体早熟程度和粒子自身适应度值自适应调整惯性权重的策略，针对不同的粒子分别采用不同的自适应操作，使得群体始终保持惯性权重的多样性。

其中，fg为全局最优粒子的适应度值，fap为适应度值优于当前所有粒子适应度平均值 fag的粒子的适应度平均值。Δ可用来评价粒子群的早熟收敛程度，Δ越小，粒子群越趋于早熟收敛。对于适应度值为fi的粒子，其自适应调整策略如下所示。

1)fi优于fap

此时粒子比较接近全局最优值，是群体中的较优粒子，其惯性权重应取较小值，避免“逃离”全局最优值，粒子的惯性权重按式(8)自适应调整。

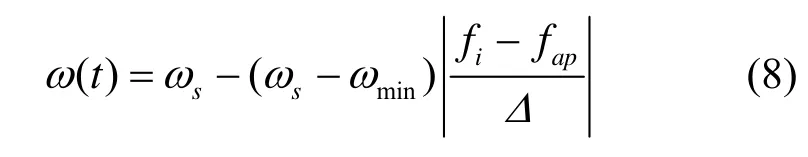
其中，ωmin为ω的最小值，sω为ω取值范围的中间值。粒子适应值越佳，其惯性权重相应越小，以加强局部寻优。

2)fi劣于fap但优于fag

此时粒子是群体中的一般粒子，具有较好的全局寻优能力和局部寻优能力，其惯性权重按式(9)所示的非线性递减策略自适应调整。

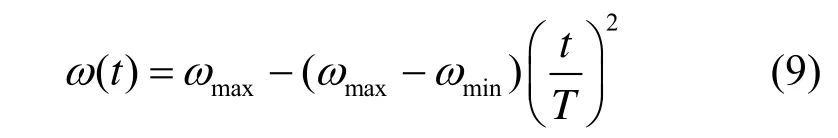
3)fi劣于fag

此时粒子是群体中较差的粒子，应赋予较大的惯性权重，其自适应调整策略为

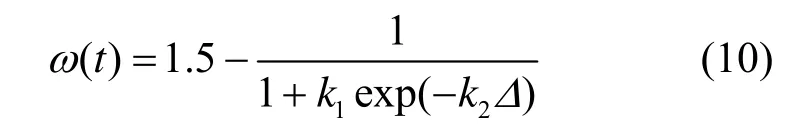
其中，参数k1＞1用于控制ω的上限，k1越大，ω的上限越大；k2＞0用于控制ω的调节能力。

4.3 非线性周期振荡参数策略

受社会群体中常发生的分散和重组交替现象（如鸟类觅食过程）的启发[10]，结合群体早熟收敛程度的概念，本文提出了一种采用非线性振荡参数策略的粒子群优化算法，使全局搜索和局部挖掘在优化过程中交替，以提高算法的全局寻优能力。

在搜索初期，采用较大的个体学习因子和较小的社会学习因子，有利于群体搜索整个空间；在搜索后期，较小的个体学习因子和较大的社会学习因子则有利于群体收敛于全局最优。因此，粒子的个体学习因子c1采用非线性递减策略，而社会学习因子c2采用非线性递增策略，其数学描述如式(11)所示。

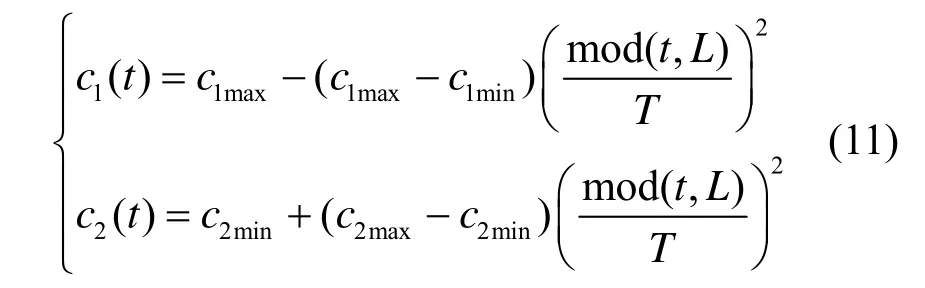
其中，c1max、c2max分别为粒子个体学习因子和社会学习因子的最大值；c1min、c2min分别为粒子个体学习因子和社会学习因子的最小值；L为振荡周期；mod(·)表示取模运算。学习因子c1、c2的变化趋势如图1所示。

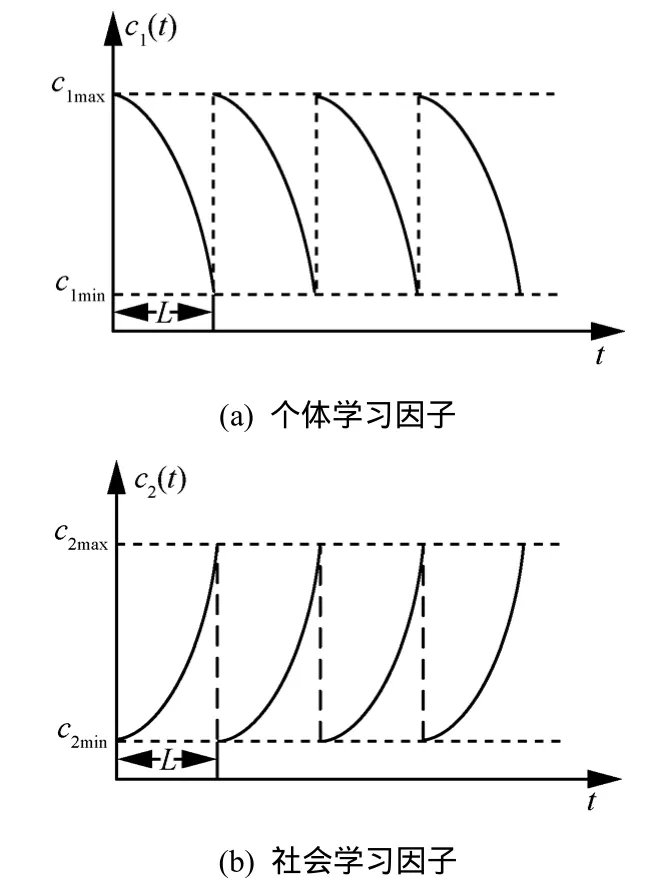
图1 粒子学习因子周期振荡策略

4.4 算法收敛性和复杂度分析

对于式(1)所示的基本粒子群算法，令φ1=c1r1，φ2=c2r2，则式(1)中的两式可合并为

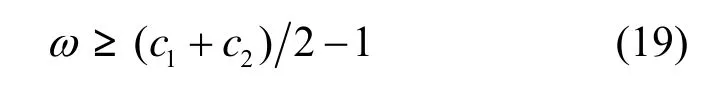
下面根据粒子群惯性权重的调整策略分3种情况对上述条件进行分析。

1)fi优于fap

综合式(8)、式(11)和式(19)，可得

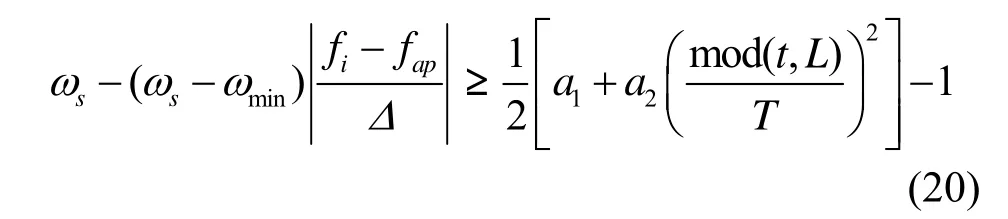
其中，a1=c1max+c2min，a2=c2max-c2min-c1max+c1min。不妨作最保守的估计，把不等式(20)的两边看作2个函数，要满足式(20)，只需满足式(20)左边函数的最小值不小于右边函数的最大值（以下简称“最小—最大”原理），经化简可得

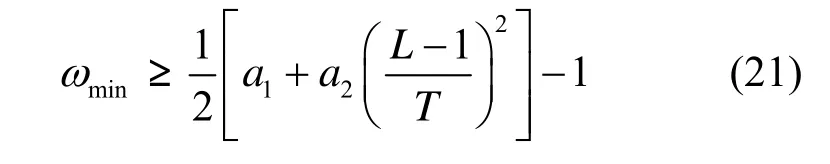
2)fi劣于fap但优于fag

综合式(9)、式(11)和式(19)，可得

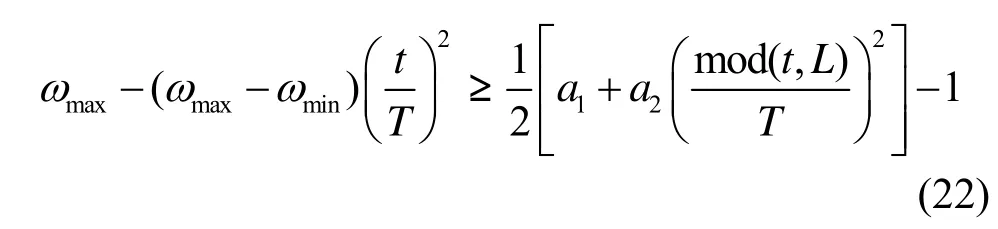
根据“最小—最大”原理，可将式(22)化简为

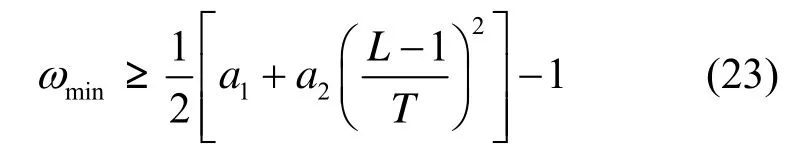
3)fi劣于fag

综合式(10)、式(11)和式(19)，可得

由k1＞1，k2＞0可知，不等式(24)左边函数的值域为(0.5,1.5)，因此，根据“最小—最大”原理，满足不等式(24)的条件为

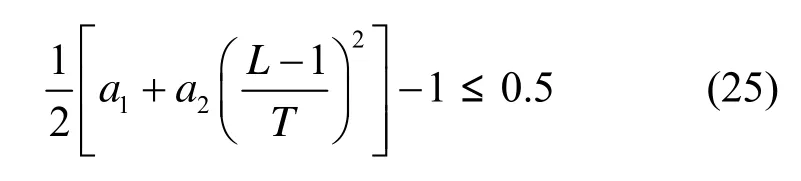
综上可得，算法收敛时参数需满足的条件为

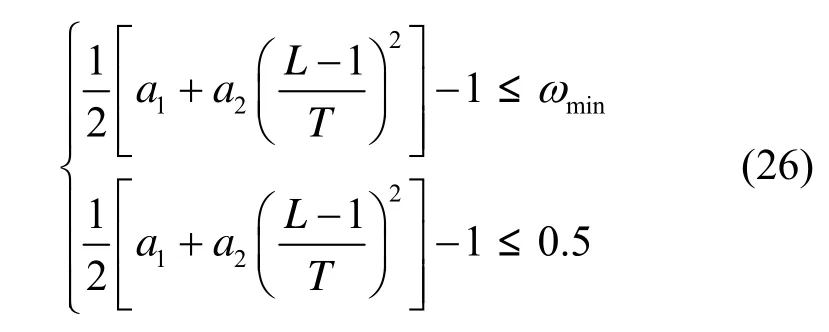
综上可知，只需选取合适的算法参数，使其满足式(26)，即可保证本文算法的收敛性。

下面分析算法的复杂度。设粒子群的规模为N，每一个粒子的维数为D，最大迭代步数为T，则混沌初始化粒子群速度和位置的计算复杂度为O(ND)。在每一次迭代运算中，找出适应度值小于所有粒子适应度均值的粒子的计算复杂度为O(N)，基于群体早熟程度的惯性权重自适应调整的计算复杂度为O(N)，采用非线性振荡策略调整粒子学习因子的计算复杂度为O(1)，更新粒子速度和位置的计算复杂度为O(ND)。因此，算法总的计算复杂度为O(ND)+O(T(N+N+1+ND))=O(TND)。

5 算法步骤及仿真验证

5.1 算法的实现步骤

根据上文中的算法原理及改进策略，本文提出的基于群体早熟收敛程度和周期振荡参数策略的混沌自适应粒子群算法的实现步骤如下。

Step1 确定粒子群规模N、最大迭代次数T和振荡周期L等参数，并根据4.1节中的方法对粒子的位置和速度进行混沌初始化。

Step2 初始化粒子群的局部最优值和全局最优值。

Step3 计算各粒子的适应度值，并根据各粒子的早熟收敛程度选择相应的策略调整其惯性权重。

Step4 采用周期振荡参数策略更新粒子的个体学习因子和社会学习因子。

Step5 更新粒子群的局部最优值和全局最优值。

Step6 若满足停止条件，停止搜索，并输出全局最优值及其适应度值；否则转向Step3。

5.2 仿真验证

为了对本文所提算法的性能进行分析和验证，选取4个典型Benchmark优化问题进行分析。根据文献[15]，粒子种群采用非对称初始化。此外，对粒子的位置和速度加以限制，防止粒子远离搜索空间。各优化函数的初始化范围和粒子取值区间如表1所示。

为了验证本文所提（简称PDNPO-PSO）算法的性能，将其与参数线性调整PSO（L-PSO，惯性权重、学习因子均线性变化）算法、参数非线性调整PSO（N-PSO，惯性权重、学习因子均非线性变化）算法、混沌粒子群（C-PSO）算法和基于群体早熟程度的自适应 PSO（PD-PSO，学习因子非线性变化）算法进行对比分析。考虑到算法每次运行的随机性，对于每个测试函数所采用的每种优化算法都重复测试 20次，取其均值作为最终的优化结果，参数的振荡周期取为L=300。对各基准测试函数的仿真结果如图2所示。

图2中的纵坐标为对最优粒子适应度值求以10为底的对数后的值。通过分析可知，对于4个基准测试函数，以上5种粒子群算法都能在有限的迭代步数内迅速向全局最优解靠拢。其中，参数线性变化策略（L-PSO）相比而言收敛速度最慢，在设置迭代步数范围内还没收敛到最优值，参数非线性变化策略（N-PSO）次之；混沌粒子群算法（C-PSO）的寻优速度和效果要优于参数线性变化和非线性变化策略的粒子群算法；基于粒子群体早熟程度的自适应 PSO（PD-PSO）算法全局寻优效果较好，能以较快的速度收敛到全局最优值，且寻优结果比较接近实际最优值；本文所提（PDNPO-PSO）算法则综合了其他各算法的优点，寻优效果最佳。

表1 基准测试函数及其参数设置

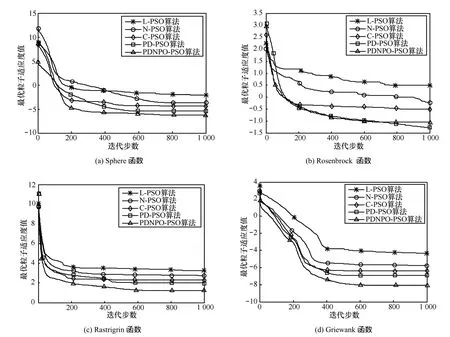
图2 基准测试函数收敛曲线

为了进一步比较以上各算法的性能，对于每一个基准测试函数，对每种算法搜索到的最优值求平均值，作为最终的全局最优值。此外，为了分析比较各算法的稳定性，分别对重复测试中每次得到的最优粒子位置的各维求标准差，然后对所有维数的标准差求和，以此作为该算法稳定性的指标，标准差越小，算法越稳定。各算法的稳定性能指标如表2所示。

由表2可知，相比其他几种PSO算法，本文提出的基于群体早熟程度和周期震荡参数策略的自适应混沌粒子群算法具有优越的全局寻优能力，对4个基准测试函数都能有效地找到最优值，且算法性能较稳定。

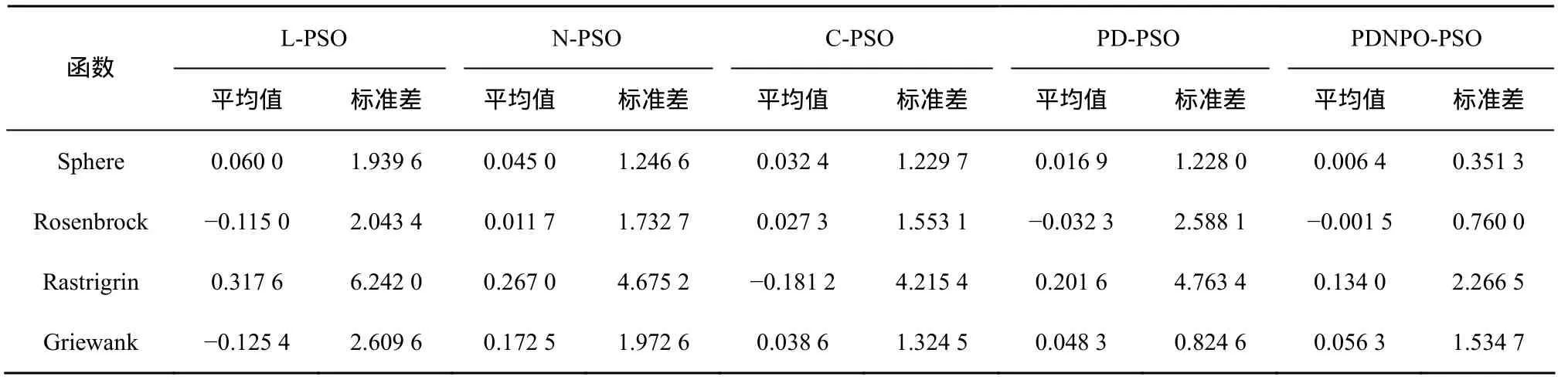
表2 各算法稳定性比较

6 结束语

本文在参考现有粒子群算法参数时变策略的基础上，结合混沌的遍历特性，提出了一种新的粒子群优化算法——基于群体早熟收敛程度和非线性周期振荡参数策略的自适应混沌粒子群优化算法。该算法首先利用混沌特性初始化粒子的速度和位置信息；惯性权重根据粒子种群的早熟收敛程度和不同适应度值的粒子自适应地采用不同的调整策略；对于学习因子的调整，则采用周期振荡策略，在每一振荡周期内学习因子非线性调整，模拟鸟类觅食过程中交替出现的分散和重组现象。经4个基准测试函数仿真验证表明，本文提出的算法不仅收敛速度快、搜索到的全局最优值质量高，而且算法具有良好的稳定性，在通信领域的优化问题中具有良好的应用前景。

[1]SIERRA M R,COELLO C A C. Multi-objective particle swarm optimizers: a survey of the state-of-the-art[J]. International Journal of Computational Intelligence Research,2006,2(3): 287-308.

[2]郦苏丹,朱江,李广侠. 采用遗传算法的低轨区域通信星座优化设计[J]. 通信学报,2005,26(8): 122-128.LI S D,ZHU J,LI G X. Optimization of LEO regional communication satellite constellation with GA algorithm[J]. Journal on Communications,2005,26(8): 122-128.

[3]闻英友,姜月秋,赵林亮等. 传感器网络中基于树的感知器分布优化[J]. 通信学报,2005,26(3): 1-6.WEN Y Y,JIANG Y Q,ZHAO L L,et al. Optimal sensor node distribution algorithm based on tree in sensor network[J]. Journal on Communications,2005,26(3): 1-6.

[4]朱剑,赵海,徐久强等. WSN中可靠通信保障下的生存周期优化问题研究[J]. 通信学报,2010,31(6): 67-73.ZHU J,ZHAO H,XU J Q,et al. Research of survival period optimization with ensuring reliable communication in WSN[J]. Journal on Communications,2010,31(6): 67-73.

[5]靳其兵,赵振兴,苏晓静. 基于粒子健康度的快速收敛粒子群优化算法[J]. 化工学报,2011,62(8): 2328-2333.JIN Q B,ZHAO Z X,SU X J. PSO algorithm with high speed convergence based on particle health[J]. CIESC Journal,2011,62(8): 2328-2333.

[6]SHI Y H,EBERHART R C. A modified particle swarm optimizer[A].Proc of IEEE International Conference on Evolutionary Computation[C].Anchorage,Alaska,USA,1998.69-73.

[7]STACEY A,JANCIC M,GRUNDY I. Particle swarm optimization with mutation[A]. The 2003 Congress on Evolutionary Computation[C].Camberra,Australia,2003.1425-1430.

[8]张利凤,胡小兵. 求解非线性约束问题的混合粒子群优化算法[J].计算机科学,2011,38(10A): 178-180.ZHANG L F,HU X B. Hybrid particle swarm algorithm of solving nonlinear constraint optimization problems[J]. Computer Science,2011,38(10A): 178-180.

[9]李军军,甘世红,许波桅. 基于伪幂函数的离散粒子群算法及其应用[J]. 控制理论与应用,2011,28(6): 834-838.LI J J,GAN S H,XU B W. Discrete particle swarm optimization algorithm based on pseudo power function and its applications[J]. Control Theory & Applications,2011,28(6): 834-838.

[10]张治俊,罗辞勇,张帆等. 采用振荡参数策略的粒子群优化算法[J].重庆大学学报,2011,34(6): 36-41.ZHANG Z J,LUO C Y,ZHANG F,et al. Particle swarm optimization with oscillating parameter strategy[J]. Journal of Chongqing University,2011,34(6): 36-41.

[11]王爽心,韩芳,朱衡君. 基于改进变尺度混沌优化方法的经济负荷分配[J]. 中国电机工程学报,2005,25(24): 90-95.WANG S X,HAN F,ZHU H J. Economic load dispatch based on improved mutative scale chaotic optimization[J]. Proceedings of the CSEE,2005,25(24): 90-95.

[12]王瑞琪,张承慧,李珂. 基于改进混沌优化的多目标遗传算法[J].控制与决策,2011,26(9): 1391-1397.WANG R Q,ZHANG C H,LI K. Multi-objective genetic algorithm based on improved chaotic optimization[J]. Control and Decision,2011,26(9): 1391-1397.

[13]吴浩扬,朱长纯,常炳国等. 基于种群过早收敛程度定量分析的改进自适应遗传算法[J].西安交通大学学报,1999,33(11): 27-30.WU H Y,ZHU C C,CHANG B G,et al. Improved adaptive genetic algorithm based on the quantificational analysis of swarm premature convergence degree[J]. Journal of Xi'an Jiaotong University,1999,33(11): 27-30.

[14]刘洪波,王秀坤,谭国真. 粒子群优化算法的收敛性分析及其混沌改进算法[J]. 控制与决策,2006,21(6): 636-640.LIU H B ,WANG X K,TAN G Z. Convergence analysis of particle swarm optimization and its improved algorithm based on chaos[J].Control and Decision,2006,21(6): 636-640.

[15]段其昌,黄大炜,雷蕾. 带扩展记忆的粒子群优化算法仿真分析[J]. 控制与决策,2011,26(7): 1087-1100.DUAN Q C,HUANG D W,LEI L. Simulation analysis of particle swarm optimization algorithm with extended memory[J]. Control and Decision,2011,26(7): 1087-1100.