基于非线性复扩散耦合冲激滤波器的图像放大算法研究.

席志红，海涛,2

(1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001；2.南阳师范学院 物理与电子工程学院，河南 南阳 473000)

1 引言

图像放大是一种提高图像分辨率的处理方法，又称单幅图像超分辨率重建，具有较高的实用价值。传统线性图像放大方法如：最近邻域方法、双线性插值方法、双三次插值方法具有运算速度快的优点，缺点是图像高频即边缘部分重建效果较差[1]。非线性放大方法能够较好地重建图像边缘部分，如基于边缘插值的图像放大方法[2]。最近，正则化方法广泛用于图像非线性放大，如采用变换域正则化方法实现图像放大[3]，采用偏微分方程直接在时域实现图像放大[4,5]，前者的处理图像不考虑抗混叠滤波器，后者的处理图像考虑抗混叠滤波器。考察待处理低分辨率图像获取模型中是否有抗混叠滤波器，对应的放大算法也可分为2种情况，其中，对光电转换设备获取图像作为低分辨率图像进行放大，必须考虑抗混叠滤波器，如照相机的点扩散函数(PSF，point spread function)相当于抗混叠滤波器，本文放大算法的处理图像考虑抗混叠滤波器。

Guichard F提出连续图像退化模型[1,5]：v=h*u(i′,j′)。其中，u 是原始图像，v是得到的低分辨率图像，h为低通抗混叠滤波器，(i′,j′)为低分辨率图像的量化操作。用一个离散的高分辨率图像 u(i,j)作为连续图像u的近似，h(i,j)作为h的离散化处理，上述模型变为如下离散模型。

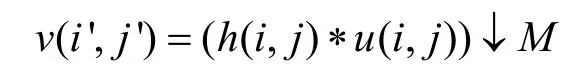
其中，↓为下采样。该模型没有考虑噪声，加上噪声的低分辨率图像模型为

用字典排序方法将 v(i′,j′)、u(i,j)、n(i′,j′)分别排列成列向量，用v、u、n表示，同样方法H表示包含下采样操作M的h(i,j)，可分别得到2种模型的矩阵表示方法：v=Hu，v=Hu +n。

近年来，采用偏微分方程方法进行图像放大取得了较好的放大效果[4]，这些算法针对无噪模型设计，没有考虑式(1)加噪声的退化图像模型。复扩散模型具有易于得到扩散图像的二阶导数的特点，利用图像的二阶导数耦合冲激滤波器，具有增强边缘的同时保持图像中斜坡结构的优点[6,7]。本文改进了复扩散模型在扩散初期边缘和细节为线性扩散的缺点，并用于图像放大。本文算法根据像素的局部方差自适应决定扩散参数，消除平滑部分噪声，保持边缘，同时使用自适应冲激滤波器增强边缘。

2 复扩散耦合冲激滤波器

Gilboa G和 Sochen N提出复扩散[6]

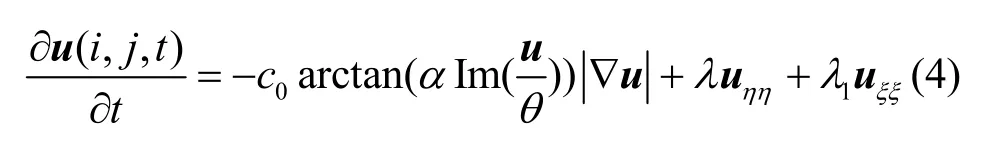
其中，arctan()为反正切函数，Im()为取虚部运算，c0、α 为正实数，θ的取值保证实部为正，λ=|λ|ejθ,−π/2＜θ＜π/2，λ1为正数。式(4)中，在梯度方向以|λ|线性正向扩散，虽然可以保持斜坡结构，边缘仍被模糊。为此Ludusan C提出混合冲激滤波器[9]，本文提出了另一种方案解决此问题，并用于图像放大。

3 基于复扩散耦合冲激滤波器的图像放大

基于偏微分方程的图像放大算法[4～6]先对退化图像进行线性插值放大作为初始图像，进行非线性扩散的同时采用不同方法实现约束模型。非线性处理的任务是增强被模糊的初始图像边缘，光滑由于初始图像放大而造成边缘的锯齿效应，实现约束模型的作用是限制得到的图像逼近真值图像。本文对无噪声图像放大和有噪声图像放大问题进行讨论，采用复扩散耦合冲激滤波器的偏微分方程方法增强边缘和双正交映射实现约束模型。

3.1 改进复扩散模型的无噪放大算法

放大图像无噪声或者噪声较小时，改进的复扩散放大算法如式(5)所示。

σw2(i,j)是以(i,j)邻域的局部方差，w为窗口大小。k针对图像特征自适应改变：细节边缘部分局部方差较大，k为较小值；平滑部分局部方差较小，k为较大值。G是H关于下采样M的双正交滤波器矩阵表示，即G满足HG=I。式(5)右边的前三项为正则项，对图像边缘和细节进行非线性增强，最后一项为保真项，对放大图像进行双正交映射操作，确保放大图像满足无噪图像退化模型。式(5)中第一项为局部曲线梯度方向的扩散，d1(Im(u))为改进的扩散系数，由式(3)可知，d1(Im(u))消除了扩散时间对式(2)中d(Im(u))的影响，使式(5)在局部曲线梯度方向一直保持非线性扩散。式(5)第二项为沿局部曲线切线方向的扩散，扩散系数λ1为常数，用来平滑边缘放大产生的锯齿效应。式(5)第三项为基于复扩散的冲激滤波器对边缘进行锐化，相对于式(4)的复扩散冲激滤波器，使用代替消除了扩散时间对冲激滤波器的影响。最后一项为采用双正交滤波器G的保真项，分步实现正则项和保真项，可保证得到的图像完全满足约束模型[10]。

3.2 自适应非线性复扩有噪放大算法

对于加噪声的图像模型如式(1)，偏微分方程放大算法[4～6]很少考虑噪声，利用复扩散在扩散开始时线性扩散具有较强的去除噪声特点，放大的同时提高对噪声的顽健性，放大算法如式(6)所示。

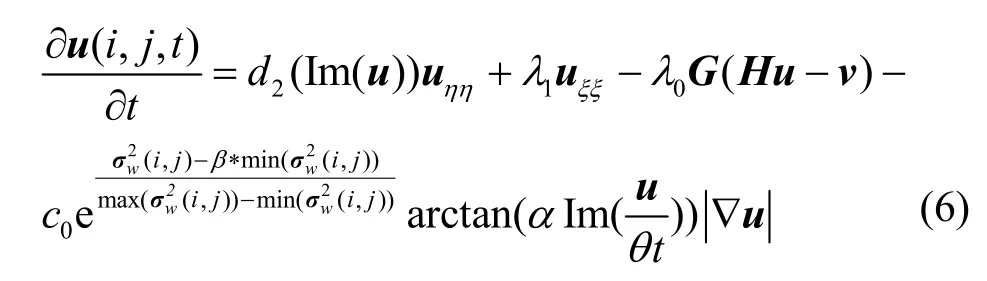
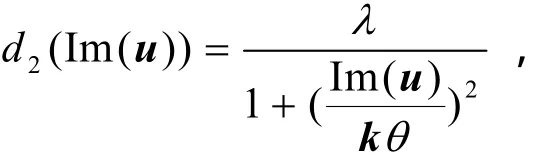
式(6)第三项为改进的冲激滤波器，其强度受局部方差约束而自适应改变，即使在扩散初始阶段，边缘和细节部分也能够自适应地增强。Dong Y Q采用置信区间方法给出噪声的最大局部方差估计Bw,m=τσ2(w为局部方差的窗口，m为w内像素总数，σ2为退化图像真实噪声方差)，τ值与m和图像像素总数有关[11]。退化图像像素局部方差大于Bw,m时，该像素以概率P是细节或边缘部分，给出了P=0.8558时τ的具体数值曲线，m=7×7时，τ ≈ 2.25。由于本文中σ2每次扩散后发生变化，用最小局部方差近似σ2，实际上σ2要略小于min(σw2(i,j))，因此τ值是本文β取值的上限，在认为最小局部方差所在窗口内只有噪声的情况下，可以得到β的取值下限为1，因此1≤β≤2.25。β越大则判定细节和边缘的准确性越高，同时漏判的细节和边缘也越多，β越小准确性越低，同时漏判也越少，噪声误判为细节增多，本文β取值为1.5。需要指出，式(6)中第一项在扩散初始时刻为线性扩散，在一定程度上弥补β取值较小带来的缺陷。式(6)中第四项为保真项，作用为实现约束模型，λ0取决于噪声方差，其他扩散系数也受方差影响。

4 自适应复扩散耦合自适应冲激滤波器图像放大算法实现

总结对无噪图像和有噪图像放大算法的具体实现。

对无噪声图像放大，本文对正则项和双正交映射操作分步执行，其中，由H得到关于采样矩阵双正交的滤波器G，满足HG=I。迭代实现以u0为初始图像，即 u0=(((v)↑M)﹡G)，迭代实现如式(7)所示。

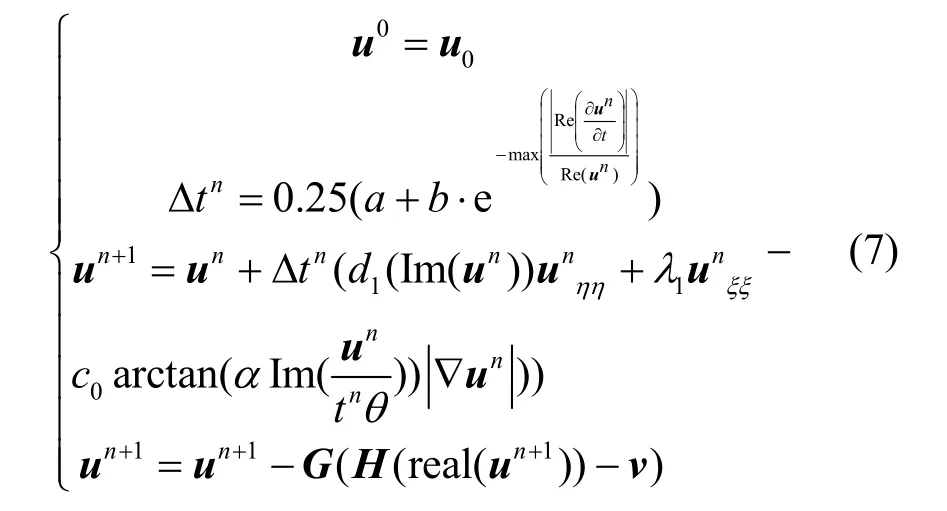
其中，最后的式子为双正交映射实现，结合初始图像和每次迭代的双正交映射操作，可以保证得到的图像即扩散结果的实部满足约束条件，即 v(i′,j′)=(h(i,j)﹡u(i,j))↓M，矩阵表示：v=Hu。用数学归纳法证明如下。

n=0时，u0=u0=Gv，

由HG=I，Hu0=H(Gv)=HGv=v

假设Hun=v成立，证明n=n＋1也成立。

应用双正交条件HG=I，

H(real(un+1))=H{real[un+1−HG(H(real(un+1))−v)]}=H(real(un+1))−HG(H(real(un+1)))+HGv=v

证毕。

式(7)中的d1(Im(u))如式(5)所示，4倍放大时参数取值为c0=0.5，α=1，θ≤π/10，对于无噪图像(σ≤1)，d1(Im(un))中|λ|=λ1∈[0.02,0.05]可以取得较好的效果。

有噪声图像放大算法迭代实现如式(8)所示，同样以 u0为初始图像，即 u0=(((v)↑M)·G)。

4倍放大时对应参数设定为c0=0.5，α=1，θ≤π/10，λ0、λ1和 d2(Im(un))中的 λ受退化图像噪声方差 σ2约束(σ≥1)：|λ|=λ1∈[0.02σ,0.05σ]，噪声越大，正则项扩散系数越大，λ0∝1/σ2。由图 1可以看出，局部方差窗口越大，包含噪声的平滑部分局部方差越小，同时边缘部分变粗，因此需要选择合适的窗口值，本文选择窗口大小为7×7。2种算法中 a+b≤1,本文取 a=0.25,b=0.75，采用诺曼边界条件，Δt是时间步长，n是迭代次数。Araújo A证明了复扩散稳定性条件[12]，Bernardes R证明了采用变步长复扩散满足式(8)中Δt的稳定性[13]。

图1 不同窗口尺寸局部方差

5 实验结果及分析

为了与其他方法比较，设计以下实验方案：选择高分辨率无噪图像作为参考图像，图2所示为本文仿真的参考图像（方框部分显示放大效果），对参考图像进行抗混叠低通滤波和下采样操作，对得到的低分辨率图像进行放大和加噪声后放大。抗混叠滤波器h设定为一个σ0=0.5的3×3高斯低通模板(实际的h由图像获取硬件特性决定)[14]。

h由一维滤波器h1=(0.1063,0.7874,0.1063)的张量积得到，h1关于2倍下采样双正交滤波器为[10]g1=(−0.0339,0.2511,0.5656,0.2511,−0.0339)，张量积可得二维滤波器g，矩阵表示为G。对得到的低分辨率图像进行放大处理，仿真中本文算法参数为：c0=0.5，α=1，θ=π/10，|λ|=λ1=0.035，4 倍放大扩散时间为2.5 s，为了保证参数的一致性，16倍放大采用两次4倍放大级联实现，每次参数不变。最近，基于模型的图像放大算法效果较好的有Aly等提出的基于改进的总变差(TV,total variation)算法[15](简称AD算法)、Roussos等提出的算法简称RM算法[4]、Getreuer P提出的放大算法[16](简称PG算法)和Xi等提出的放大算法[10](简称XH算法)。仿真实验中为了保证比较的公平性，AD算法、XH算法直接采用退化滤波器h，PG算法中参数PSF取[0.135,0]，是h的一维滤波器h1对h1(2)归一化的结果，因此也是同一退化滤波器，RM算法的特点是要求放大算法中的h方差要小于真实退化滤波器的方差，因此取σ=0.45，略小于本文退化滤波器h方差0.5。AD的其他参数λ=0.05，error=0.01Δt=0.1，XH算法采用文献[10]中的参数数值。

图2 参考图像

图3是部分Lena图像局部图像的4倍放大。观察图像帽檐和帽子与脸部相接的 3条边缘，AD算法图中3条边缘被模糊，边缘的横向过渡带相对于参考图像被拉长，RM算法边缘本身虽然有较好的效果，但在强边缘的邻域却出现过增强的阴影形状，PG算法边缘存在稍微的模糊效果，XH算法对边缘模糊有一定的改善，明显看出本文算法能够较好地逼近原始图像的对应边缘，边缘定位最好。

图4为部分Peppers图像的局部图像16倍放大，观察边缘部分，AD算法得到的图像边缘模糊更明显，RM算法得到的图像强边缘阴影形状更明显。PG算法结果中强边缘附近出现杂乱的虚假纹理，这主要因为PG算法采用小波滤波器组实现约束条件，当对边缘的高频部分进行较多补偿时（16倍放大），小波滤波器组对高频部分的相位错位造成的。本文算法的16倍放大结果的边缘效果也是最好的，图3中在其他细节部分如眼睫毛的放大效果，本文算法也是最好的，进一步验证了本文算法具有较好的性能。

图3 4倍部分Lena图像的局部图像放大

图5是在不加噪声和加σ=10的零均值高斯噪声情况下，使用图2作为参考图像得到的不同算法的峰值信噪比(PSNR,peak signal to noise ratio)和平均结构相似性测度(MSSIM,mean structural similarity measure)[17]。

PSNR在平方意义上反映放大图像和参考图像的误差，其定义为式(9)所示，MSSIM 侧重于反映参考图像和放大图像在边缘细节的误差。图5(a)和图5(c)在无噪声情况下，本文算法具有最高的PSNR，本文算法中包含较多细节图像的 MSSIM 稍小于RM算法，主要由于RM算法放大的初始图像是频域零插值方法得到，能够保留退化图像的全部细节部分，但强边缘存在由于吉普斯效应增强后造成的波纹阴影；而平滑图像如部分Peppers的MSSIM本文算法则最高。

图4 部分Peppers图像16倍放大比较

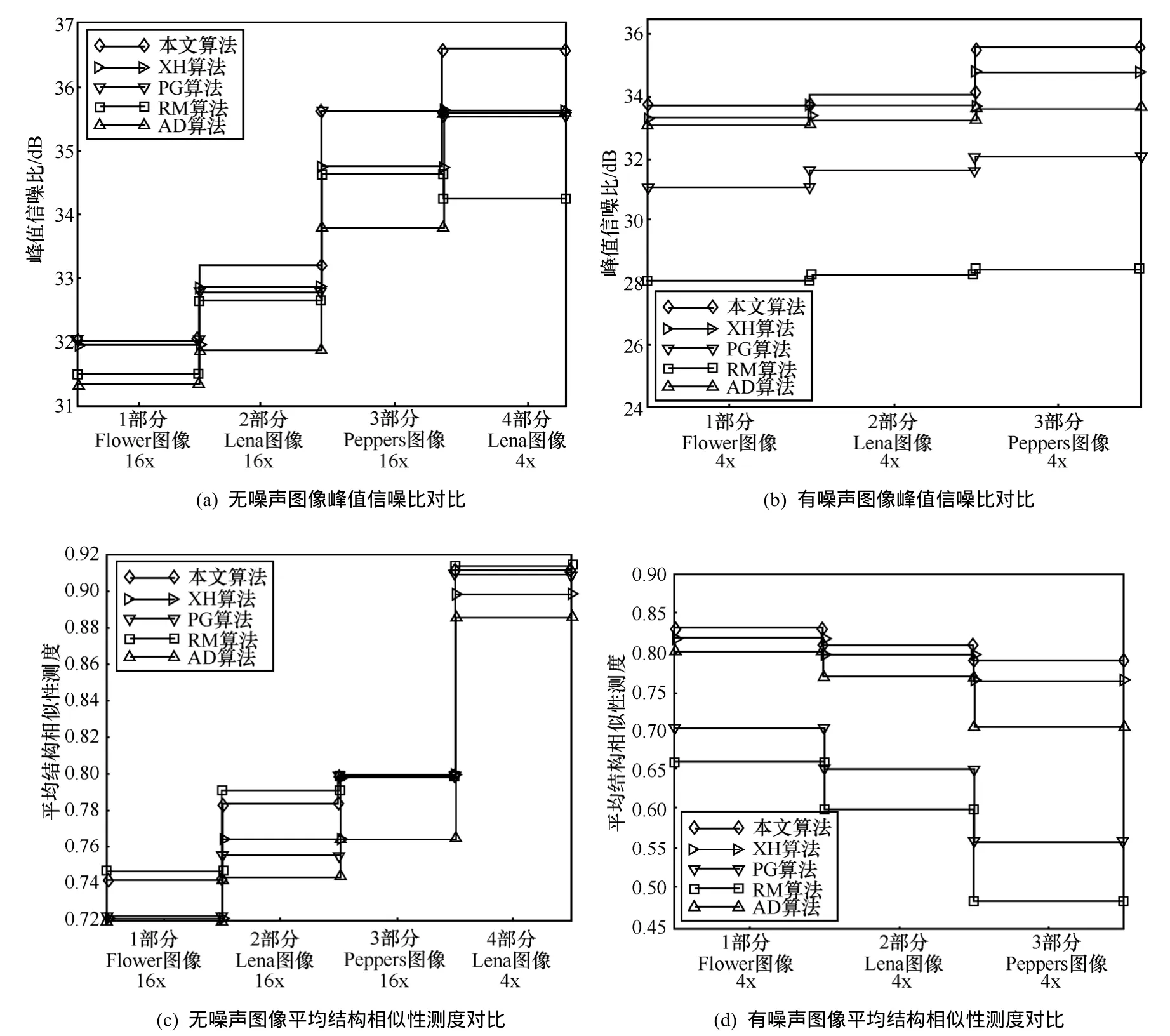
图5 算法峰值信噪比和平均结构相似性测度比较

图6为退化下采样后的图像加σ=10的零均值高斯噪声后，进行4倍放大的结果。PG算法和RM算法在平滑的窗框上出现错误的纹理，对噪声图像放大的视觉效果都比较差，PG算法边缘较RM算法受噪声影响小一些。AD算法结果显示有一定的去除噪声能力，但边缘也被模糊。XH算法和本文算法的结果最接近，但还是弱于本文算法去除噪声能力，并且其边缘效果也不如本文算法。图5(b)和图 5(d)为峰值信噪比和平均结构相似性测度的比较，可见本文算法无论在视觉效果还是峰值信噪比和平均结构相似性测度比较上本文算法都是最好，反映了本文算法在加噪声情况下具有较好的性能。

图6 局部Flower噪声(σ=10)图像放大

分析XH算法原理是低梯度部分正向扩散，中高梯度部分逆扩散，因此随着噪声强度的增强，其去噪性能必定减弱，因此，σ=15的高斯噪声图像进行仿真比较如图7所示，可以看出XH方法抗噪能力明显下降，而本文算法可以较好地去除噪声，同时保持较强边缘，图7(b)验证了复扩散可以较好地保持斜坡结构并去除噪声。

图7 σ=15的噪声图像放大

6 结束语

本文提出了基于非线性复扩散耦合复冲激滤波器的图像放大算法，无噪声放大算法和有噪声放大算法都具有较好的效果，由于采用复扩散冲击滤波器，对边缘的增强效果较好，解决了边缘错位问题。无噪声图像放大算法中，本文采用梯度方向改进的非线性复扩散，在整个扩散过程中均为非线性扩散，同时受局部方差约束，能够较好地保持边缘和小边缘，冲激滤波器的幅度与二阶导数Δu有关，有效地锐化了边缘。算法引入了双正交映射，使得放大图像的视觉效果更好，并且相对于其他算法有较高的峰值信噪比。有噪声图像放大算法以局部方差对扩散系数和冲激强度进行自适应约束，在消除噪声的同时增强边缘；扩散初始阶段的近似线性扩散能够去除噪声但同时平滑了微小边缘，局部方差的自适应约束处理方法能够在一定程度上弥补这一不足。需要指出的是，本文算法采用自适应步长扩散，为保证方法的稳定性，本文采用的扩散步长Δt相对于临界步长有较大的富裕量。确定一个合适的扩散时间是放大算法在实际应用中的一个重要问题，对于4倍图像放大的扩散时间，本文设定参数取2～3 s是合适的，对于任意倍数放大扩散时间的闭式确定是本文算法的一个难题，是今后工作改进的方向。

[1]MALGOUYRES F,GUICHARD F. Edge direction preserving image zooming: a mathematical and numerical analysis[J]. Journal of Numerical Analysis,2001,39(1):1-37.

[2]LI X,ORCHARD M T. New edge-directed interpolation[J]. IEEE Transactions on Image Processing,2001,10(10):1521-1527.

[3]MALLAT S,YU G S. Super-resolution with sparse mixing estimators[J]. IEEE Transactions on Image Processing,2010,19(11):2889-2900.

[4]ROUSSOS A,MARAGOS P. Reversible interpolation of vectorial images by an anisotropic diffusion-projection PDE[J]. International Journal of Computer Vision,2009,84(2):130-145.

[5]BELAHMIDI A,GUICHARD F. A partial differential equation approach to image zoom[A]. Proceedings of International Conference on Image Processing[C]. Washing DC,USA,2004.649-652.

[6]GILBOA G,SOCHEN N,ZEEVI Y Y. Image enhancement and denoising by complex diffusion processes[J]. IEEE Transactions Pattern Analysis and Machine Intelligence,2004,26(8):1020-1036.

[7]GILBOA G,SOCHEN N,ZEEVI Y Y. Zeevi,regularized shock filters and complex diffusion[A]. European Conference on Computer Vision 2002,Lecture Notes in Computer Science[C]. Springer Berlin Heidelberg,2002. 399-413.

[8]OSHER S,RUDIN L. Feature-oriented image enhancement using shock filters[J]. SIAM Journal on Numerical Analysis,1990,27:919-940.

[9]LUDUŞAN C,LAVIALLE O,TEREBEŞ R. Image enhancement using hybrid shock filters[A]. 2010 IEEE International Conference on Automation Quality and Testing Robotics (AQTR)[C]. 2010.1-6.

[10]席志红，海涛，肖易寒.多尺度模型结合改进前向后向扩散的图像放大[J]. 计算机辅助设计与图形学学报，2012,24(9):1197-1203.XI Z H,HAI T,XIAO Y H. Image enlargement based on multi-scale model coupling of the improved forward-and-backward diffusion[J].Journal of Computer-Aided Design and Computer Graphics,2012,24(9):1197-1203.

[11]DONG Y Q,HINTERMÜLLER M,MONSERRAT RINCON-CAMA -CHO M. Automated regularization parameter selection in multi-scale total variation models for image restoration[J]. Journal of Mathematical Imaging and Vision,2011,40(1):82-104.

[12]ARAÚJO A,BARBEIRO S,SERRANHO P. Stability of finite difference schemes for complex diffusion processes[J]. SIAM Journal on Numerical Analysis,2012,50(3):1284-1296.

[13]BERNARDES R,MADURO C,SERRANHO P. Improved adaptive complex diffusion despeckling filter[J]. Optics Express,2010,18(23):24048-24059.

[14]ALY H A,DUBOIS E. Specification of the observation model for regularized image up-sampling[J]. IEEE Trans on Image Process,2005,14(5):567-576.

[15]ALY H A,DUBOIS E. Image up-sampling using total-variation regularization with a new observation model[J]. IEEE Transactions on Image Processing,2005,14(10):1647-1659.

[16]GETREUER P ,STENCILS C. Total variation along curves for adaptive image interpolation[J]. SIAM J on Imaging Sciences,2011,4(3):954-979.

[17]WANG Z,BOVIK A C,SHEIKH H R. Image quality assessment:from error visibility to structural similarity[J]. IEEE Trans on Image Processing,2004,13(4):600-612.