基于McmC的新安江模型参数不确定性分析及应用

2014-10-26毕诗咏

陕西水利 2014年1期

毕诗咏马静

（吉林省水文水资源局延边分局吉林延吉 133001）

1 研究背景

水文预报精度在很大程度上取决于流域水文模型参数的优选和检验，现有的水文预报的模型都是概念性水文模型，水文模型的参数大多具有明确的物理意义，从理论上应该是可以通过实测来确定的。但是由于缺乏实测值，现有的模型主要是对实际水文物理过程的概化，很多待定的模型参数并不是反映单一过程或者单一影响因素的结果，因此不大可能通过实测来进行确定，只能依靠系统分析方法，采用最优化技术进行求解[1]。人们常采用的试算法以及客观优选法主要依赖于人的经验，因此，所选的参数常因人而异，且费时费力。在求解结构复杂且参数比较多的模型时，采用传统的最优化方法会出现局部最优的问题，难以确保得到的参数全局最优，而且求解步骤比较繁琐。因此，流域水文模型的参数优选工作一直都是一个大家关注的重点以及难点问题[2]。本文将结合Mcm C方法对新安江模型参数不确定性进行分析。

2 McmC方法

MCMC（Markov Chain Monte Carlo）方法源自于物理学研究，MCMC 方法是根据Bayesian推断为中心的后验分布来模拟随机样本的一种动态的蒙特卡洛方法[3]。

MCMC 方法的核心思想是构造一个概率转移矩阵，建立一个以分布π（x）为平稳分布的Markov 链来得到π（x）的样本，产生若干条独立并行的Markov 链来探索模型参数空间，通过不断更新样本信息而使Markov 链收敛于高概率密度区，也就是Bayesian 方法中的最大后验估计[4]。Mcm C方法中的Metropolis-Hastings取样方法能够更有效的探索未知参数空间，因此本文采用Mcm C方法推求新安江模型参数的后验分布及其预测区间。

2.1 常用的MCMC采样方法

MCMC 方法基于Bayesian 理论，通过建立以π（x）为平衡分布的马尔可夫链，并对其分布进行采样，通过不断的更新样本信息使得马尔可夫链能够充分的搜索模型的参数空间，最终收敛到高概率密度区域。因此，MCMC 方法是对理想的Bayesian 推断过程的一种近似[5]。常用的MCMC 采样方法有：Gibbs 采样方法和Metropolis-Hastings 方法。

2.2 McmC方法的实施步骤

实施步骤概括为如下三步：

Step1：在状态空间D上建立一个以 π（x）为平稳分布，转移核为(p·，·)的Markov链；

Step2：由D中某一点X（0）出发，用Step1中的Markov链产生点序列X（1），L，X（n）；

Step3：对某个m和足够大的n，用式（1）估计任一函数f(x)：

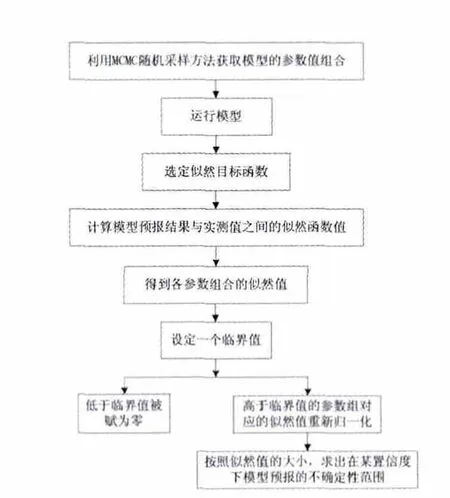
图1 McmC的水文模型参数不确定性分析流程

表1 参数的取值范围

表2 参数后验分布

3 实例分析

将Mcm C方法应用到新安江模型，采用东洋河流域1963年～1988年10场历史洪水进行研究，应用Mcm C方法对由模型参数引起的模型输出不确定性进行估计。

本例中Mcm C方法采用的参数为：新安江模型参数个数n=15；种群规模pops=400；线程数p=8；初始进化代数n=10；最大循环次数L=50000。

3.1 确定参数的初始范围和先验分布函数

一般情况下，参数的先验分布形式不容易确定，因此常常采用均匀采样或者对数采样等方式进行代替，本文采用均匀分布。

3.2 基于MCMC的不确定性分析

通过对敏感性分析选定的新安江模型的SM、KG、KSS、KKSS、GS、WDM这六个参数进行分析，由Mcm C方法获取30000个参数组，设置目标函数值的阈值为0.7，选择高于阀值的所有参数组，并设置为有效参数组，然后对有效参数组分别进行计算，得到计算流量值，按照似然值的大小进行排序，并设定置信水平为90%（置信度上限95%，下限为5%）的模型计算不确定性区间。

表2中的最小值以及最大值与表1中的参数搜索范围基本一致，说明采用Mcm C方法进行不确定性研究，参数空间得到了有效的搜索。

图2给出由MCMC方法得到的东洋河流域新安江模型的参数SM、KG、KSS、KKSS、CS、WDM的边缘分布，每个刻度对应的纵坐标值表示该参数值落在该刻度值和前一刻度值之间的概率。

图2给出了由MCMC方法抽样得到的东洋河流域新安江模型的六个参数的边缘分布，每刻度对应的纵坐标值表示该参数值落在该刻度与前一刻度值之间的概率。由图2可以看出，SM、KG、KSS、KKSS、CS、WDM这六个参数都有明显的分布规律。第二章中的优选值SM=17.517、KG=0.2817、KSS=0.4134、KKSS=0.6157、CS=0.2001、WDM=78.5762大致落在图2中各对应参数概率最大的区域，由此可以看出Mcm C方法得到的结果和D E算法是一致的。MCMC方法不仅可以给出模型各参数的后验分布，而且可以识别参数空间内概率最大的区域。

图2 新安江模型各参数边缘后验分布直方图

采用Mcm C方法达到收敛以后抽取的新安江模型的SM、KG、KSS、KKSS、CS、WDM六个参数的2000个参数组样本对东洋河流域的19820801号、19830907号、19880814号历史洪水分别进行模拟，可生成三场洪水的2000个模拟流量数据，再根据求得的模拟数据求出流量分布函数，并且求出该分布的5%和95%分位数作为其水文预报的90%不确定性置信区间。图3到图5给出了东洋河流域新安江模型模拟三场洪水的90%置信度的不确定性区间。

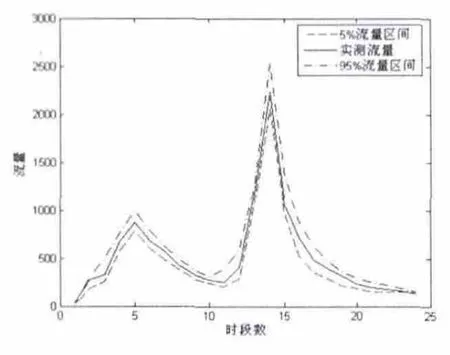
图3 东洋河流域19820801场次洪水的不确定性范围

图4 东洋河流域19830907场次洪水的不确定性范围

图5 东洋河流域19880814场次洪水的不确定性范围

图3给出了198208号洪水实测流量过程、水文预报90%不确定性区间。图4给出了198309号洪水实测流量过程、水文预报90%不确定性区间。图5给出了198808号洪水实测流量过程、水文预报90%不确定性区间。由图3、图4和图5可以看出，不确定性范围在不同时间段是不同的，随流量而变，在高流量区较大，在低流量区较小。模拟得到的流量过程线的上、下边界并不能完全包含实测流量过程线，总有一些实测流量落在90%的置信区间之外，并不能完全模拟流域的流量过程。但不确定性范围基本包含了实测流量过程的多数，说明新安江模型在东洋河流域的应用是可行的，模型结构本身误差所产生的不确定性影响在可接受范围内。