中国股市流动性深度日内模式——基于马尔科夫调制泊松过程模型

王春峰 ， 熊春连，2， 房振明， 黄晓彬

(1. 天津大学管理与经济学部， 天津 300072； 2. 天津城建大学理学院， 天津 300384; 3. 渤海证券股份有限公司， 天津 300381)

中国股市流动性深度日内模式
——基于马尔科夫调制泊松过程模型

王春峰1， 熊春连1，2， 房振明3， 黄晓彬1

(1. 天津大学管理与经济学部， 天津 300072； 2. 天津城建大学理学院， 天津 300384; 3. 渤海证券股份有限公司， 天津 300381)

针对已有流动性深度日内模式的研究数据受异常事件污染的局限，基于马尔科夫调制泊松过程，构建了交易量分离模型，该模型可分离交易量中的异常交易量。进一步以交易量为流动性深度的代理指标，研究了中国股市的流动性深度日内模式。研究发现：异常交易量确实对我国股市的深度日内模式有影响；由于对信息的敏感程度不同，不同规模股票的深度日内模式不同，对信息敏感的中、小市值股票具有W型模式，而对信息相对不敏感的大市值股票呈U型模式；由于不同市场走势下，投资者对市场信息的敏感程度不同，我国股市深度日内模式受市场走势的影响，牛市时，深度日内模式呈U型，而熊市时，深度日内模式呈W型。

流动性； 深度； 日内模式； 马尔科夫调制泊松过程

证券市场流动性是证券市场的生命力所在。对证券市场流动性模式的研究一方面能够揭示信息传导和价格发现过程的本质，寻找市场运行的规律，另一方面能为投资和监管提供重要的依据和参考。因此，对证券市场流动性模式的研究始终是证券市场微观结构研究领域的重要问题之一。

在微观结构的研究中，流动性通常包括四个维度：宽度、深度、弹性和及时性。流动性模式的研究主要集中于宽度和深度两个维度。有关流动性深度模式研究主要集中于三个方面：第一，针对交易量和换手率等交易指标的日内和周内模式分析[1-2]；第二，利用高频报价交易数据，构建复杂的高频报价交易指标，分析不同交易机制下不同证券市场的流动性深度模式[3-6]；第三，从信息的角度出发，将信息与流动性变化模式相结合，探讨流动性变化的本质原因[7-8]。

可见，已有研究沿着构建各种不同的流动性深度代理指标，考察不同交易机制下不同证券市场的流动性深度模式及产生原因的方向发展。但存在几点不足：首先，已有的研究都是基于一些受异常事件(如金融危机爆发、突发性的宏观事件及突发性的公司事件等)污染的观测数据，而这些异常事件很可能会造成研究结果偏误。这就不难解释为什么不同市场甚至相同市场，研究者得出的流动性深度模式不同；其次，已有文献未区分不同规模股票的流动性深度模式，证券市场的实践表明，不同规模股票的交易活跃程度具有很大不同，把不同规模股票的流动性深度模式混合起来研究可能很难得出真实的结论；最后，已有的研究局限于整个样本期，未区分牛市和熊市时的流动性深度模式。不同市场态势下投资者的行为不同，如风险厌恶程度、投资者情绪等不同，而市场流动性深度水平极大地受投资者的这些行为影响。

基于马尔科夫调制泊松过程，本文构建一个交易量分离模型，该模型可以将交易量中的异常交易量分离出来，从而得到不受异常事件污染的交易量数据，这克服了以往研究都以受异常事件污染的交易数据为研究对象的局限。进一步，基于构建的交易量分离模型实证研究我国股市的流动性深度模式。首先，研究我国股市的流动性深度模式是否受异常交易量数据影响；其次，研究我国股市牛市和熊市时的流动性深度日内模式是否相同；最后，研究不同规模股票的流动性深度日内模式是否相同。本文的研究不仅扩展了数据分离方法在交易量的研究领域的应用，而且丰富了我国股市流动性模式的研究，所建构的交易量分离模型为开展交易量的相关研究奠定了基础。

一、交易量分离模型的构建与参数估计

马尔科夫调制泊松过程(Markov modulated Poisson process，MMPP)是一个泊松过程，其瞬时泊松到达率是一个平稳的随机过程，且受到另一个泊松过程的调制，这另一个泊松过程的发生与否取决于一个不可观测的隐马尔科夫过程所处的状态。由MMPP产生的数据是观测数据，而由隐马尔科夫链产生的数据则是隐数据。马尔科夫调制泊松过程和隐马尔科夫链近年来在资产定价、价格行为及期权定价等金融领域逐步得到应用。Easley和O’hara(2011)[9]在研究中提出了交易量服从泊松分布的假设，这为将马尔科夫调制泊松过程进一步应用到分离证券市场交易量中的异常交易量奠定了基础。本文将交易量看作一个隐马尔科夫调制泊松过程产生的观测数据，将异常事件的发生看作是隐一个马尔科夫链，这个隐马尔科夫链产生的数据即是异常交易量数据。具体地，我们采用Scott[10]的马尔科夫调制非齐次泊松过程模型建模交易量，进而分离交易量中的异常交易量。具体建模步骤如下。

将时间t的股票交易量N(t)看作异常交易量(异常事件引起的交易量)N1(t)和剔除异常交易量后的交易量N0(t)的叠加。即N(t)=N0(t)+N1(t),其中N(t)、N0(t)及N1(t)均大于等于0的整数。

1. 剔除异常交易量后的交易量N0(t)的建模

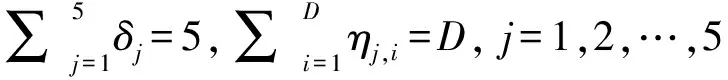
根据贝叶斯统计推断的原理，本文选择共轭先验分布作为变量λ0、δ、η的先验分布，从而保证后验分布具有与先验分布相同的分布形式，进而为后面的统计推断带来方便。即假设

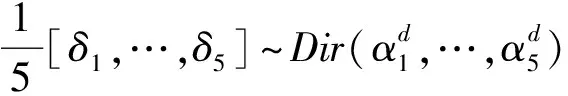
2. 异常交易量N1(t)的建模

异常事件引发异常交易量，但不可通过交易数据观测到。本文把异常事件z(t)看作是一个具有2个状态的一阶隐马尔科夫过程，即

其中Dir(·)为Dirichlet分布。当z(t)≠0时，假设N1(t)服从到达率为γ(t)的非齐次泊松过程。即

其中P(·)为泊松分布。

因γ(t)为泊松分布的参数，而泊松分布的共轭先验分布是伽马(Gamma)分布，故假定γ(t)～Γ(γ,aγ,bγ)。N1(t)的泊松分布中，N和γ均未知，但可通过下面式(1)的积分化简得到N1(t)的边际分布。

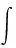
(1)

其中NBin(·)为负二项分布。因此当z(t)≠0时，可以通过随机模拟的方法生成服从负二项分布的异常交易量N1(t)。

3. 模型参数的估计

本文采用马尔科夫链蒙特卡罗模拟方法完成模型参数的估计及相关变量的数值模拟。其过程分为四步。

第一步，给定N0(t)，估计λt的三个参数λ0、δ、η，从而获得λt的估计， 首次计算时以观测序列N(t)代替N0(t)；第二步，给定N(t)、λt、Mz估计状态z(t)，首次计算时状态转移概率矩阵Mz取先验值；第三步，根据步骤二得出的z(t)，计算z(t)各个值之间的转移频率，从而获得Mz各个元素的值，进而更新Mz；第四步，给定N(t)、λt、z(t)，采用MCMC的方法估计N0(t)、N1(t)。然后不断循环上述四个步骤，直到各参变量取值满足收敛标准时停止。最后通过如下两个手段评价模型估计的效果：第一，估计参数的稳定性；第二，构建包含所有参数的似然函数，根据似然值评价。由于篇幅所限，以上具体的估计过程参考Scott[10]等、Ihler[11]等的研究。

二、数据描述与实证方法

1. 样本选择与数据

本文整个样本区间为：2007.7.16—2008.1.18，共135天；牛市期为2007.7.16—2007.10.12；熊市期为2007.10.22—2008.1.18。牛市和熊市各占65天。选取中证800指数中的284只股票作为样本股票，其中84只股票选自中证100指数，100只股票选自中证200指数，另外100只股票选自中证500指数，它们分别代表大、中、小规模的股票，全部样本则代表整个中国股市。中证100中只选取了84只股票是因为在样本期，只有这些股票一直保留在中证100中，其他选取的股票在样本期则一直保留在相应的指数中。

学术界对流动性深度衡量目前尚缺乏统一标准，基于交易量的流动性衡量方法是较常使用的一种方法，本文以交易量为流动性深度衡量指标。采用国泰安高频分笔交易量数据。以5分钟为时间窗口加总交易量，从而把每日交易时段9：30—11：30和13：00—15：00的交易量数据分为48个时间段数据，这样在整个样本期，每只股票样本得到一个5分钟加总的交易量序列，序列长度为130×48=6 420，整个样本的数据总数为284×130×48=1 772 160。

2. 实证方法

本文基于构建的交易量分离模型将交易量中的异常交易量分离出来，并在此基础上研究我国股市的流动性深度日内模式。

第一步，基于构建的交易量分离模型将284只样本股票的5分钟交易量序列N(t)分离为N0(t)和N1(t)，其中N1(t)是异常交易量，而N0(t)是剔除异常交易量后的交易量。

第二步，在全样本期间，将上述全部样本股票的N(t)和N0(t)依次按股票及交易日和交易时段取平均，得到全样本期间全部股票N(t)和N0(t)的日内模式，即得到我国股市剔除异常交易量前后的深度日内模式。画出它们的日内模式图，并观察它们的图形是否有差异，最后统计上检验剔除异常交易量前后的深度日内模式是否显著。如果研究结果发现N(t)和N0(t)的日内模式有显著差异，则说明我国股市的流动性深度日内模式受异常交易量的影响，因此研究我国股市的流动性深度日内模式应剔除交易量中的异常交易量。下面第三步和第四步的研究都是在得出我国股市的流动性深度日内模式受异常交易量影响的基础上展开的。

第三步，在全样本期间，将大、中和小规模样本股票的N0(t)分别按第二步的方法取平均，得到全样本期间的大、中和小规模股票的N0(t)的日内模式，即得到我国股市不同规模股票的流动性深度日内模式。画出它们的日内模式图，并观察它们的图形是否有差异，最后统计上检验不同规模股票的流动性深度日内模式是否显著。

第四步，在牛市和熊市时，分别将全部样本股票的N0(t)按第二步的方法取平均，得到牛市和熊市时N0(t)的日内模式，即得到我国股市牛市和熊市时的流动性深度日内模式。画出它们的日内模式图，并观察它们的图形是否有差异，最后统计上检验牛市和熊市时的流动性深度日内模式是否显著。

为了检验上述各种研究情形下的流动性深度日内模式的显著性，建立如下回归模型：

(2)

式中：ln(Vt)为对上述各种情形下的5分钟交易量序列取对数；TD为交易时段t的虚拟变量。

为了避免多重共线性，回归方程中去除第9个交易时段虚拟变量T9，因本文日内交易时段共分为48个，因此，该回归方程中共47个虚拟变量。各虚拟变量的取值如下：若Vt是日内第1个时段对应的5分钟交易量，则此时T1取1，否则取0，以此类推；βD为虚拟变量TD前的系数；εt为误差项；c为常数项。本文采用最小二乘法进行回归参数估计,并采用LM检验误差项的自相关性，若存在自相关则采用广义差分的方法克服自相关，即用AR(P)模型修正回归方程残差序列的自相关。此外，还采用怀特检验是否存在异方差，若存在异方差则采用加权最小二乘法进行回归参数的估计。若误差项既存在自相关又存在异方差时则采用加权最小二乘法AR(P)组合程序来校正异方差和自相关。下文仅仅报告回归系数和一些关键统计量的结果。

三、实证结果与分析

1. 整个样本期剔除异常交易量前后的深度日内模式

图1是整个样本期剔除异常交易量前后的深度日内模式图，从该图可知，整个样本期的N(t)、N0(t)的日内模式均呈现W型，早晨和中午开盘及下午收盘时的深度相对较大，似乎整个样本期全样本的深度模式受异常事件的影响并不大。但N(t)、N0(t)的这种W型日内模式在统计上是否均显著，剔除异常交易量前后的深度日内模式是否有显著差异呢？为此，我们根据式(2)对整个样本期的N(t)、N0(t)进行回归。对N(t)回归时，回归方程中的Vt取整个样本期284只样本股票的5分钟交易量序列N(t)的平均值序列；对N0(t)回归时，回归方程中的Vt取整个样本期284只样本股票的剔除异常交易量后的5分钟交易量序列N0(t)的平均值序列。

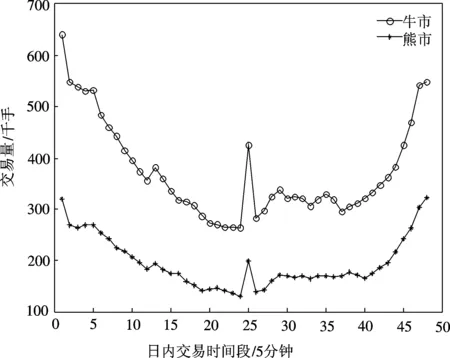
图1 N0(t)和N(t)的日内模式

表1是整个样本期剔除异常交易量前后整个股市的深度日内模式的回归结果。从表1可以发现，未剔除异常交易量的回归系数除变量T25、T43、T44及T45前的不显著外，其他在1%显著性水平下均显著，而显著的日内虚拟变量前的系数表明，日内早晨开盘和下午收盘时段前的系数较大，开盘后，随着交易进行，日内时段的系数逐渐变小，到中午收盘附近达到最小，下午开盘后，日内时段的系数又逐渐变大，因此，未剔除异常交易量的深度模式整体大致呈 U型；剔除异常交易量的回归系数除变量T44和T45前的不显著外，T25前的系数在5%显著性水平下显著，其他系数在1%显著性水平下均显著，而显著的日内虚拟变量前的系数表明，日内早晨开盘和下午收盘时段前的系数较大，开盘后，随着交易进行，日内时段的系数逐渐变小，到中午收盘附近达到最小，下午开盘后5分钟的系数突然变大，然后有一小段时间的系数变小，最后日内时段的系数又逐渐变大，因此，剔除异常交易量的深度模式整体大致呈W型。可见，剔除异常交易量前后的深度日内模式存在差异，这表明研究我国股市的流动性深度日内模式确受异常事件的影响。因此，有关流动性深度日内模式的研究有必要剔除交易量中的异常交易量。基于此，后面我们分别研究剔除异常交易量后不同规模股票和不同市场态势下的深度日内模式。

2 .整个样本期剔除异常交易量后不同规模股票的深度日内模式

前文表明，我国股市的流动性深度日内模式研究确有必要剔除交易量中的异常交易量，这里对剔除异常交易量后不同规模股票的深度日内模式进行研究。

图2是剔除异常交易量后的大、中和小规模股票在整个样本期的深度日内模式。从该图可知，剔除异常交易量后的大规模股票的深度显著大于中、小规模股票的深度，且大规模股票的深度日内模式似乎也不同于中、小规模股票的深度模式，大规模股票呈现更陡峭的W型模式，而中、小股票则呈现更扁平的W型模式。

为了从统计上检验剔除异常交易量后的大、中和小市值股票的深度日内模式是否存在差异，我们根据式(2)对整个样本期不同规模股票的N0(t)进行回归。对大市值股票的N0(t)回归时，回归方程中的Vt由所有剔除异常交易量后的大市值股票的5分钟交易量序列N0(t)取平均得到；对中、小市值股票的N0(t)回归时，回归方程中的Vt的取法与此类似。

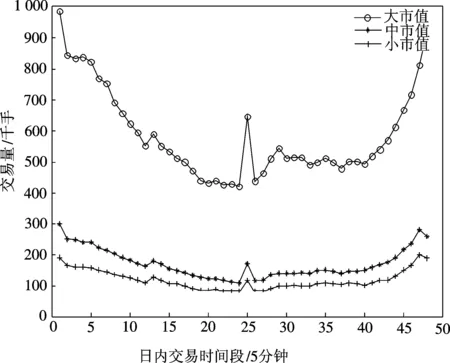
图2 整个样本期不同规模股票的N0(t)的日内模式

表2是剔除异常交易量后不同规模股票的深度日内模式的回归结果，该结果表明：大规模股票回归系数除变量T25、T44及T45前的不显著外，其他在1%显著性水平下均显著，与表1的分析类似，根据显著的日内虚拟变量前的系数，可以得出剔除异常交易量后大规模股票的深度日内模式大致呈U型；而中、小规模股票的所有回归系数在1%显著性水平下均显著，同样根据显著的日内虚拟变量前的系数，可以得出剔除异常交易量的深度日内模式两者均大致呈W型模式。

中、小规模股票剔除异常交易量的深度日内模式整体呈W型模式，可用Brock和Kleidon(1992)[12]的周期性需求增加理论解释。首先，由于存在周期性的晚间休市期，知情投资者和不知情投资者为了避免这段时间所带来的风险，在下午收盘时调整其投资组合，导致交易需求增大，深度也明显增大；而在早晨开盘时，一方面，不知情交易者周期性的资产组合调整，导致交易需求增加，另一方面，由于隔夜信息的存在，知情投资者基于信息的交易需求增加，从而深度明显增大。另外，对于短暂的中午休市期，由于这段时间给投资者带来的风险相对较小，因此，中午收盘时投资者的资产组合调整未见明显增加，从而深度未见明显增加；而中午开盘时，由于中午休市所积累的信息，导致知情投资者基于信息的交易需求增加，深度增加，但这较早晨的深度的增加要小。而大市值股票产生U型深度日内模式的原因可能是，相对于中小市值股票而言，大市值股票对信息的反应不够敏感，从而在中午开盘时的基于信息的交易需求增加不显著。

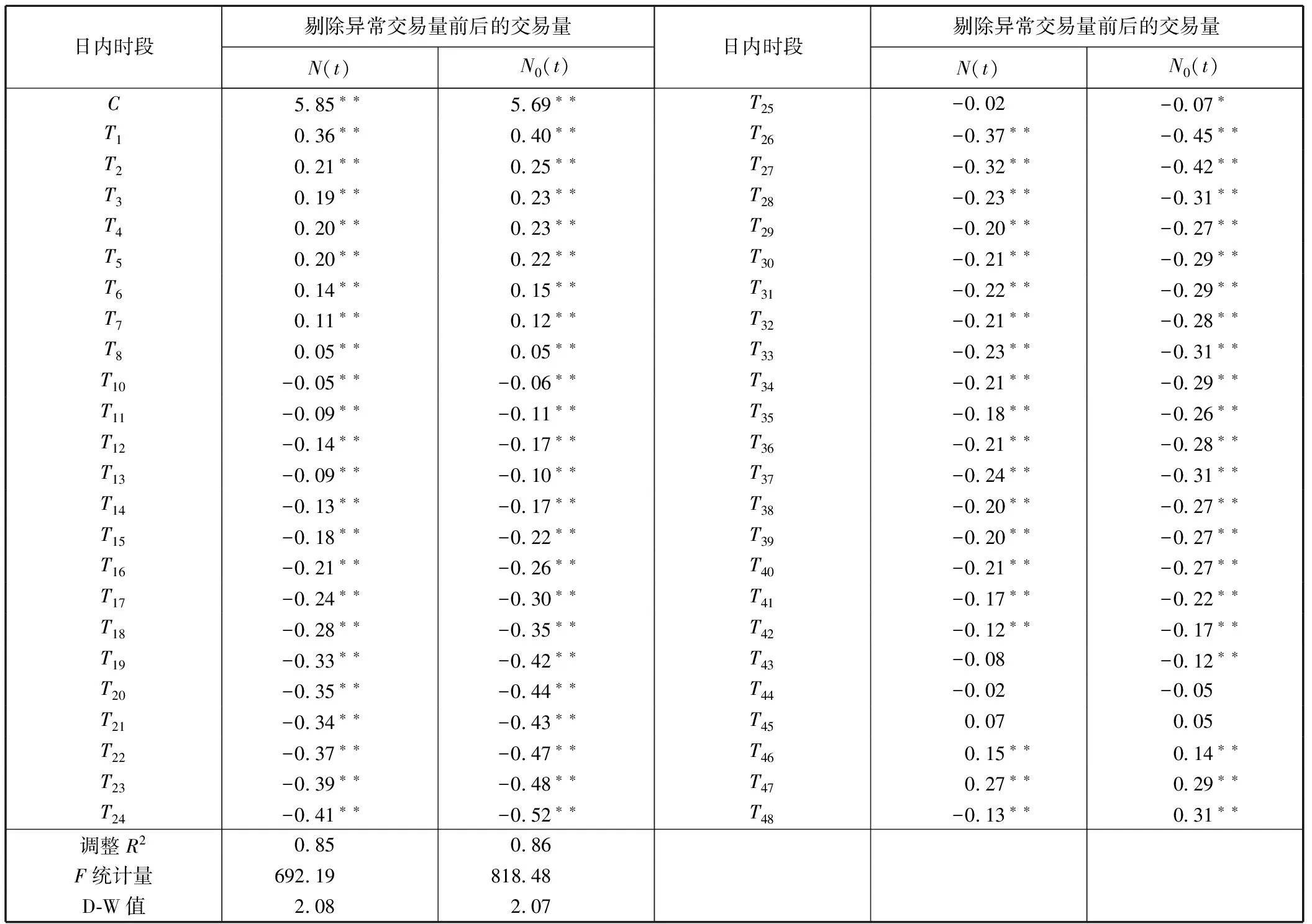
表1 剔除异常交易量前后的日内深度回归

注：**、*分别表示在1%和5%的水平下显著

3. 剔除异常交易量后不同市场态势下的深度日内模式

同样，由于前文表明，我国的流动性深度日内模式研究确有必要剔除交易量中的异常交易量，这里对剔除异常交易量后不同市场态势下的深度日内模式展开研究。

图3是剔除异常交易量后全部样本股票在牛市和熊市时的深度日内模式。从该图可知，牛市期的股票深度明显大于熊市期的股票深度，但牛市和熊市期的股票深度日内模式形状相似，均表现为早晨和中午开盘及下午收盘附近深度相对较大，且均呈现W型，所不同的是熊市时中午开盘深度增加幅度较牛市时更大。

为了从统计上检验剔除异常交易量后牛市和熊市时的我国股市深度日内模式是否存在显著差异，根据式(2)对整个样本股票在牛市和熊市时的N0(t)分别进行回归。对牛市的N0(t)回归时，回归方程中的Vt是对牛市时全样本股票剔除异常交易量后的5分钟交易量序列N0(t)取平均得到的平均值序列；而对熊市的N0(t)回归时，Vt的取法与此类似。

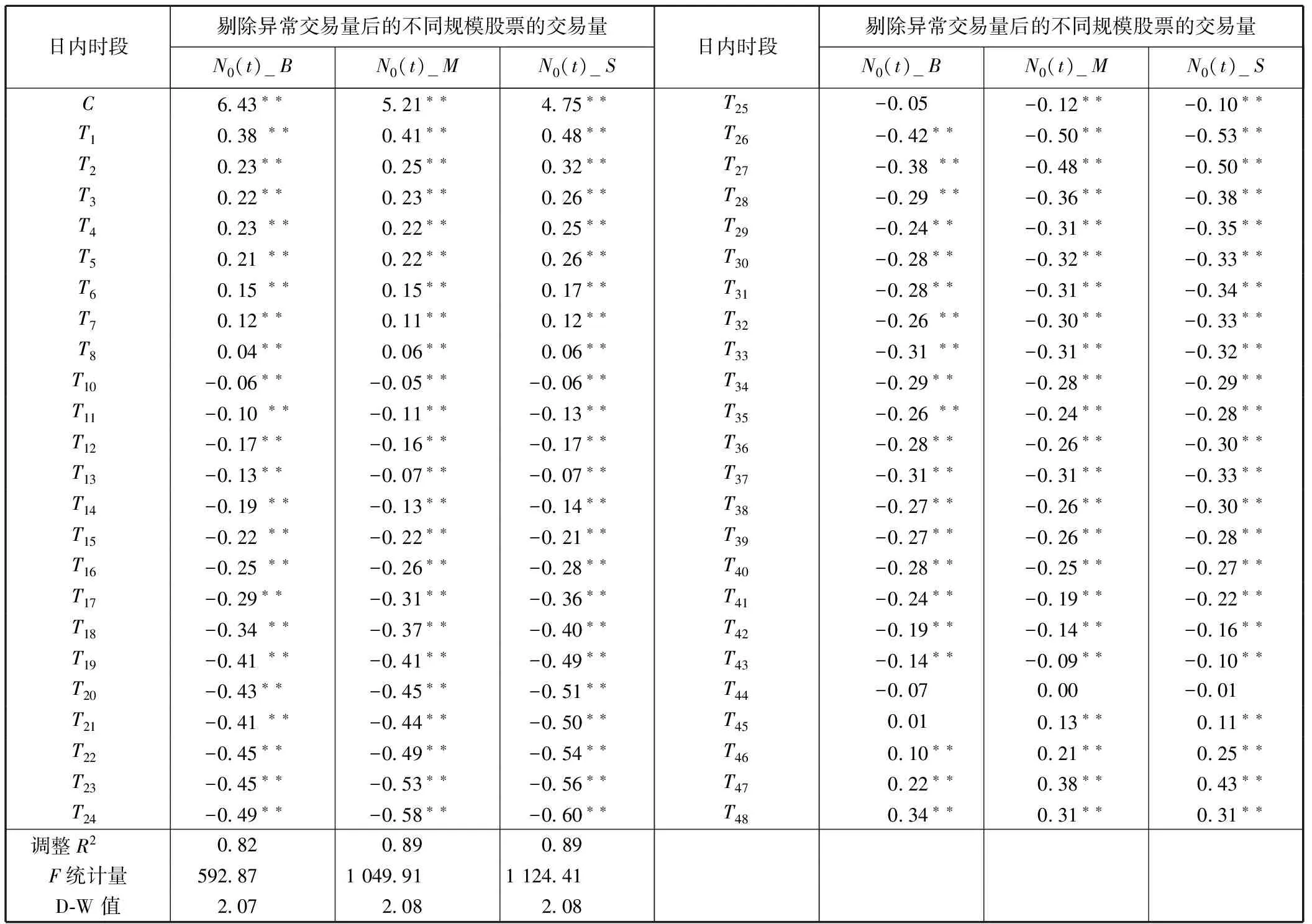
表2 剔除异常交易量后不同规模股票的日内深度回归

注：“**”、“*”分别表示在1%和5%的水平下显著；N0(t)_B、N0(t)_M、N0(t)_S分别代表大、中、小规模股票的N0(t)。

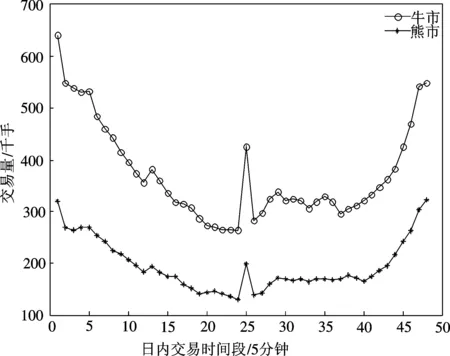
图3 牛市和熊市时N0(t)的日内模

表3是剔除异常交易量后牛市和熊市时的深度日内模式回归结果，该结果表明：牛市时，回归系数除变量T8、T25、T44及T45前的不显著外，其他在1%显著性水平下均显著，与表1的分析类似，根据显著的日内虚拟变量前的系数，可以得出剔除异常交易量后的牛市深度日内模式大致呈 U型；而熊市时，回归系数除变量T8、T44及T45前的不显著外，其余回归系数在1%显著性水平下均显著，同样根据显著的日内虚拟变量前的系数，可以得出剔除异常交易量后的熊市深度日内模式大致呈W型。这说明我国股市剔除异常交易量后不同市场态势下的深度日内模式存在显著差异，熊市时中午开盘深度增加幅度较牛市时增加幅度更显著。产生这一差异的原因可能是：熊市市场震荡剧烈，风险厌恶的投资者对市场信息更加敏感，从而在中午开盘时基于信息的交易需求增加显著。而牛市市场相对稳定，风险厌恶的投资者对市场信息相对不敏感，从而在中午开盘时基于信息的交易需求增加则相对不显著。

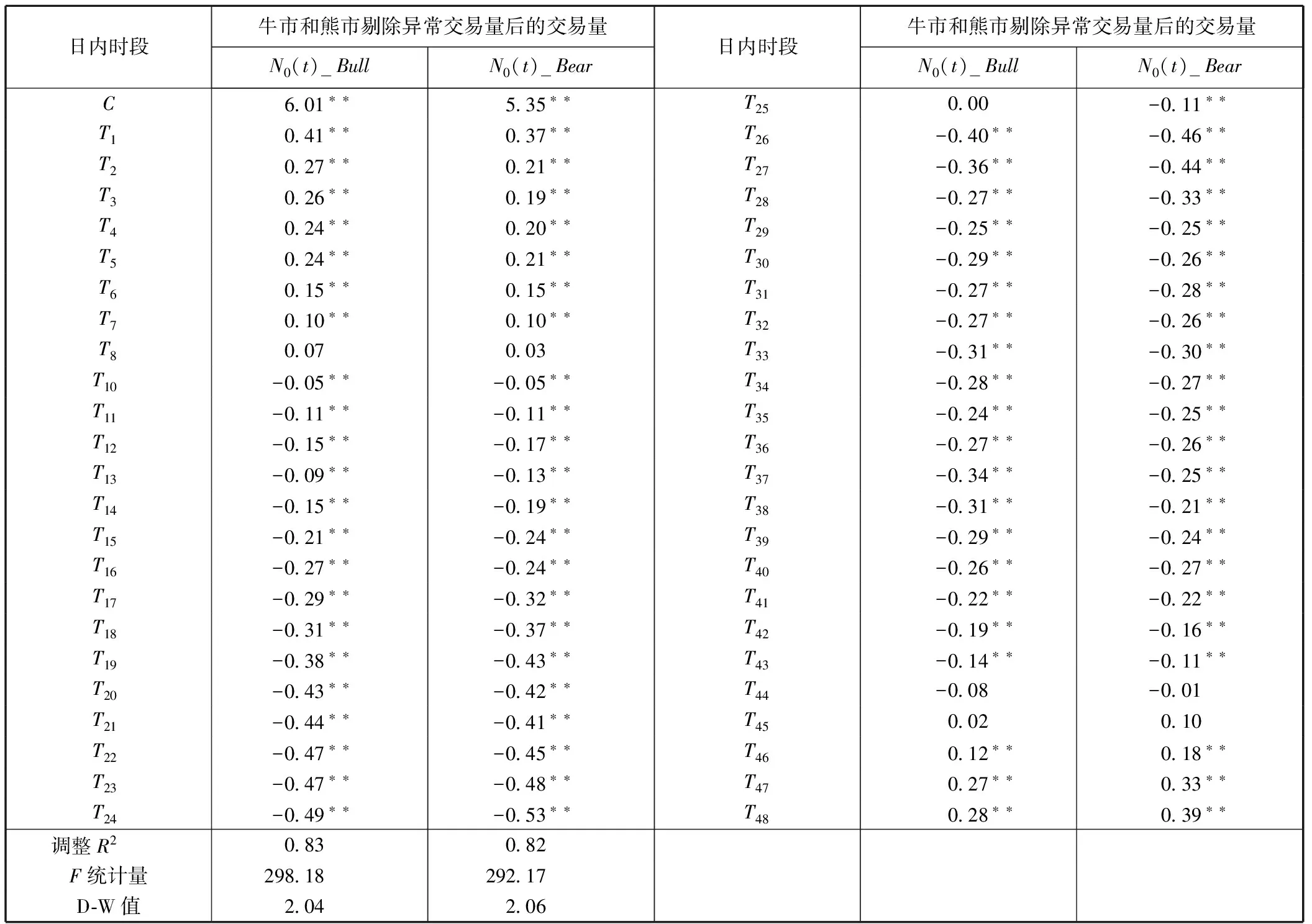
表3 剔除异常交易量后牛市和熊市时的日内深度回归

注：“**”、“*”分别表示在1%和5%的水平下显著；N0(t)_Bull、N0(t)_Bear分别代表牛市时和熊市时的N0(t)。

4. 稳健性检验

为了进一步检验结果的稳健性，本文将规模变量作为虚拟变量加入到式(2)中，以进一步检验规模变量是否对深度有显著影响。用S1、S2和S3分别表示大、中和小规模股票的虚拟变量。为了避免多重共线性，仅把变量S1和S3放入回归方程。同样，本文还将市场态势作为虚拟变量加入到式(2)中，以进一步检验市场态势是否对深度有显著影响。用M1和M2分别代表牛市和熊市虚拟变量。为了避免多重共线性，仅把变量M2放入回归方程。表4是 分别加入规模变量和市场态势变量到式(2)中的回归结果。该结果表明：S1和S3的系数是显著的，这说明规模对深度有显著影响，这进一步验证了不同规模股票的深度模式不同；M2的系数显著，这说明市场态势对深度有显著影响，这进一步验证了牛市和熊市时的深度模式不同。

四、结 语

基于马尔科夫调制泊松过程模型，构建了交易量分离模型，该模型可分离出交易量中的异常交易量。进一步研究了中国股市的流动性深度日内模式，得出以下结论：1) 异常交易量确实对我国股市的深度日内模式有影响；2) 由于对信息的敏感程度不同，不同规模股票的深度日内模式不同，对信息敏感的中、小市值股票具有W型模式，而对信息相对不敏感的大市值股票呈U型模式；3) 由于不同市场走势下，投资者对市场信息的敏感程度不同，我国股市深度日内模式受市场走势的影响：牛市时，深度日内模式呈U型；而熊市时,深度日内模式呈W型。

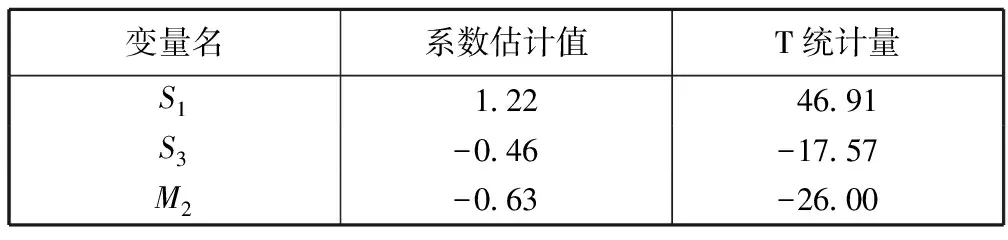
表4 稳健性检验回归

为了进一步研究我国股市的流动性深度日内模式，基于本文构建的交易量分离模型，研究牛市和熊市时不同规模股票的流动性深度日内模式是本文后续研究的一部分。

[1]Jain P, Joh G. The dependence between hourly prices and trading volume[J].JournalofFinancialandQuantitativeAnalysis， 1988, 23(3): 269-28.

[2]Foster F D, Viswanathan S. Variations in trading volume, return volatility, and trading costs： Evidence on recent price formation models[J].TheJournalofFinance，1993, 48(1): 187-211.

[3]Lee C M, Mucklow B, Ready M J. Spreads, depths, and the impact of earnings information: An intraday analysis[J].ReviewofFinancialStudies， 1993, 6(2): 345-374.

[4]Ahn H, Cheung Y. The intraday patterns of the spread and depth in a market without market makers: The stock exchange of Hong Kong[J].Pacific-BasinFinanceJournal， 1999, 7(5): 539-556.

[5]Frino A, Lepone A,Wearin G. Intraday behavior of market depth in a competitive dealer market: A note[J].JournalofFuturesMarkets， 2008, 28(3): 294-307.

[6]李子奈，杨之曙. 上海股市日内流动性:深度变化实证研究[J]. 金融研究,2003(6):25-37.

[7]Brockman P, Chung D Y. An analysis of depth behavior in an electronic, order-drivenenvironment[J].JournalofBankingandFinance， 1999, 23(12): 1861-1886.

[8]沈豪杰，黄 峰.流动性与风险管理：一个基于二元t分布GARCH估计方法的L-VAR模型[J].天津大学学报：社会科学版,2010，12(3)：197-202.

[9]Easley D, López De Prado M, O’Hara M. The microstructure of the ‘flash crash’: Flow toxicity, liquidity crashes and the probability of informed trading[J].TheJournalofPortfolioManagement, 2011, 37(2): 118-128.

[10]Scott S L, Smyth P. The Markov modulated Poisson process and Markov Poisson cascade with applications to web traffic data[J].BayesianStatistics, 2003, 7: 671-680.

[11]Ihler A, Hutchins J, Smyth P. Learning to detect events with Markov-modulated poissonprocesses[J].TransactionsonKnowledgeDiscoveryfromData, 2007, 1(3): 13-20.

[12]Brock W A, Kleidon A W. Periodic market closure and trading volume: A model of intraday bids and asks[J].JournalofEconomicDynamicsandControl,1992, 16(3): 451-489.

TheIntradayPatternsoftheLiquidityDepthinChineseStockMarkets—Based on Markov Modulated Poisson Process

Wang Chunfeng1, Xiong Chunlian1,2, Fang Zhenming3, Huang Xiaobin1

(1. Faculty of Management and Economics, Tianjin University, Tianjin 300072， China;2. Department of Basic Science, Tianjin Chengjian University , Tianjin 300384, China；3. Bohai Securities Co..Ltd, Tianjin 300381, China)

The data of the studies about the patterns of the liquidity depth in the stock markets is limited by abnormal events. To overcome this shortcoming, this paper suggests a disjunctive model about trading volume based on Markov modulated Poisson process, which separates the abnormal trading volume from the trading volume. Furthermore, it defined the trading volume to be the proxy variable of the liquidity depth and then empirically tested the intraday patterns of the liquidity depth in Chinese stock markets .The empirical results showed： the intraday patterns of the liquidity depth in Chinese stock markets are really affected by the abnormal trading volume. Due to the sensitivity of different information, different sizes of stock differs from each other in the depths of intraday patterns. Middle and small-sized stocks, sensitive to the information, show a shape of W, while large-sized stocks, unsensitive to the information, show a shape of U. Because the traders react differently when the information arrives in bull and bear markets. The intraday patterns of the liquidity depth are affected by the market trend in China: in bull market, it shows a shape of U. However in bear market, it shows a shape of W.

liquidity; market depth; intraday pattern; Markov modulated Poisson process

2013-03-01.

教育部长江学者和创新团队发展计划资助项目(IRT1028)；国家自然科学基金面上资助项目(71271146).

王春峰(1966— )，男，博士，教授.

熊春连, xiongchunlian@163.com.

F830

A

1008-4339(2014)02-097-08