用条件方程式直接探测多维粗差的方法研究

刘 利，葛永慧

（1.太原市城乡规划局 城乡建设档案馆，太原 030002；2.太原理工大学 矿业工程学院，太原 030024）

粗差是超出观测值一定限度的误差，根据偶然误差的规律性，粗差基本都大于观测值的三倍中误差。粗差出现是小概率事件，有时确实也存在，但在观测值中是极少数的，所以在进行平差计算前，应该进行粗差探测[1]。国内外测量研究人员进行了大量的理论研究，并通过大量实际案例论证，从理论和具体方法上都取得了很多可行的研究成果。通过查阅文献，这些理论和方法的基本思路一般为两种情况：一是采用待估参数计算，将粗差作为待估参数直接计算，用拟稳平差的原理解算秩亏问题，然后进行探测粗差；二是将随机选定含粗差概率小的、有验证条件的观测值当成平差计算的起算数据，运用随机选取的数据进行最小二乘法解算出待估参数，含粗差的概率较大的观测值，也就是非准观测值的残差作为粗差[2]。用第一种思路解决粗差探测问题时，又分为两种方式，第一是将极少数疑是观测值（含粗差）和一般观测值（不含粗差）看成具有相同方差、不同期望的一个基本子样，即把粗差看作是函数模型的一小部分，用这一方式最早提出一个粗差探测技术的是荷兰的巴尔达教授（Baarda）[3]；第二是将极少数的疑是观测值（含粗差）和一般观测值（不含粗差）看作具有相同方差、不同期望的一个基本子样，即把粗差当成是随机模型中的一小部分[4]。研究分析现有粗差探测的方法后不难发现，这些粗差探测的方法一要采用最小二乘法平差原理，进行经典平差解算；二要采用全面搜索、迭代重新平差计算，很多次重复计算后，才能找到粗差。这些方法搜索、迭代的次数比较多，相对运行的时间也比较长。最小二乘法原理存在均摊性的算法缺陷，直接对含有粗差的观测值进行最小二乘法计算，就会对所有观测值造成影响，达不到粗差探测的效果。为了避免最小二乘法原理的先天缺陷，笔者提出了一种新思路：将条件方程作为观测值中粗差探测的起点，把条件方程式闭合差（W）作为是否存在粗差的信号，不再做最小二乘法平差。本方法从思路、实现过程都相对简单，操作性比较强。

1 条件平差理论下的闭合差协因数阵

按照条件平差原理的数学模型，必要观测个数为t，观测值个数为n，多余观测个数为r＝n-t，列出r个条件方程式，条件平差的数学模型为：

运用最小二乘法原理VΤPV＝min，解算得观测值的改正数向量V。

由W＝-AL-A0计算出QWW协因数阵是：

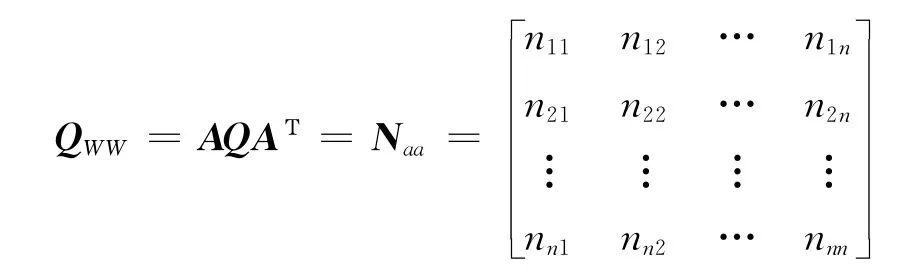
式中：QWW为闭合差W 的协因数阵；Naa为方程系数阵；Q为观测值的协因数；V为改正数向量；P为权阵；W 为闭合差向量；L为观测值向量；A0为条件式的常数列向量。

根据偶然误差理论，闭合差W可取偶然误差的极限误差，即2、3倍中误差。假设W＝2倍的中误差时，其W限差列向量为：

m0表示验后单位权中误差。

在相同观测条件下，在不考虑粗差、系统误差的情况下，W限差列向量根据偶然误差理论应服从N（0，m02Qww），即正态分布，即对i都满足

得：W可作为检验数学模型（1）成立与否的一个可靠统计值[5]。

2 条件方程式探测多维粗差法

2.1 基本原理

式中：L1，L2为观测值表示观测真值；Δ1，Δ2表示真误差。根据已知数据条件列出解算条件方程为：

式中：WⅡ为含有粗差闭合差向量，

根据平差模型，得出WⅡ中含有粗差的结论。即能够推断出，与涉及该闭合差的某些观测值中含有粗差。而且，粗差也体现在所有含有该观测值的条件方程的闭合差上。条件方程式探测多维粗差法就是根据这一总结提出来的。

2.2 实现过程

1）根据（1）式建立基础条件方程式，保存其系数阵A1。

2）根据基础条件方程式，建立完全条件方程式，保存其系数阵A2。建立完全条件方程式的基本要求为，保证观测值组成的路线在图形上是有组合意义的，即保证其路线的闭合性。

3）根据上一步的结果，搜寻闭合差

方程式，保存其系数阵A3。j为组成条件方程式的观测值个数。

4）对A3进行列变换，计算出Z的秩。含有粗差的观测值数为b＝r-Z.根据A3的秩Z≥1，推断出b≤r-1，得最多探测出r-1个粗差项。

5）计算A4，为A3的任意一组最大行线性无关组。

6）根据含有粗差的观测值在A4中的所有列向量为零，确定含有粗差观测值。

3 算例

1）有一水准网（如图1所示），高差观测值个数为n＝6，必要观测值个数为t＝3，多余观测值个数为r＝3.分别随机模拟两组含有粗差的数据见表1所示。

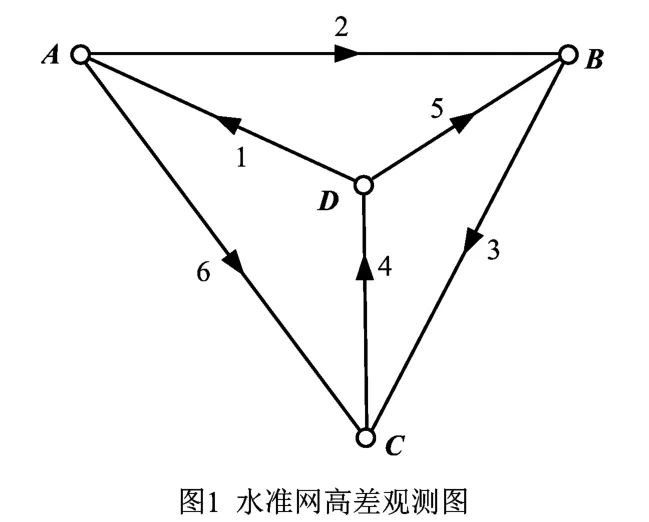
表1 模拟观测值的基本数据

采用本文方法步骤，首先由计算机自动生成观测值的偶然误差，再由

模拟出高差观测值。对含有一个粗差，且该粗差放在第一条变化的观测值上的情况进行分析，说明其解算过程。

根据上述方法，首先，计算出A1和A2，再根据

计算出A3，求A3的秩Z＝2。解算粗差个数b＝r-Z＝1。最后得出计算探测结果为第一条边含有粗差。本次算例的结果完全验证了笔者提出方法的可靠性。

将模拟粗差放在第一、第三边的观测值上，根据该方法的判断标准，检验其模拟结果也完全正确。

综上所述，笔者所验证的粗差探测方法，其原理容易理解、计算高效、实现过程简单，计算次数少、探测粗差效率高，避免了平差计算，也不需要进行反复多次迭代、搜索计算，一次计算就能够确定出观测数据中的所有粗差项。

按上述模拟数据方法，仅含一个粗差在各边上的情况，每种情况做了1000次模拟计算，其计算结果如表2所示；含两个粗差在各边上的情况，每种情况做了1000次模拟计算，其计算结果如表3（先验中误差为±3mm）。

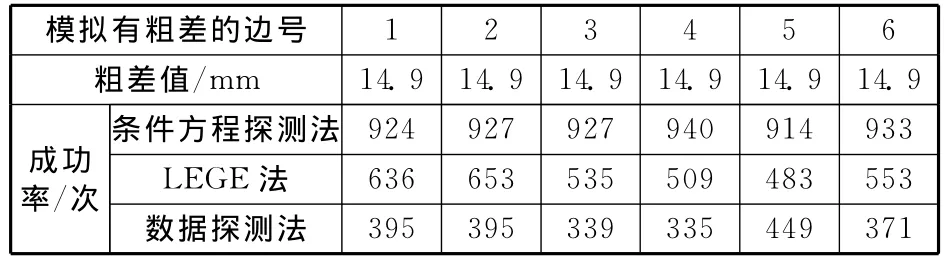
表2 仅含有一个粗差在各边上的1000次模拟计算结果

表3 含有两个粗差在各边上的1000次模拟计算结果

比较表2的数据得出，本文提出的方法能直接有效地找出粗差所在的观测值，而且成功率更高。

2）此算例来源于於宗俦教授的论文[6]，一水准网，高差观测数n＝19，必要观测数t＝10，多余观测数r＝n-t＝9，分别模拟1，2，3，4，5，6个粗差的情况（如图2所示）。

图2 模拟6个粗差观测结果

按上述方法自动生成的随机误差加入到真值，模拟出观测值，同时用LEGE法和数据探测法进行相同模拟计算，其对比如表4所示。

表4 增加粗差个数和高差观测数的数据模拟计算结果

对于LEGE法，0次搜索并没有进行，只进行最小二乘平差计算。而以后的搜索都会增加，当第k次时，共有个组合，并将组合的平差结果来修正原观测值后再进行下一次平差计算，然后一次一次迭代、搜索。此方法原理理解比较难，实现过程比较繁琐，效率也不太高。对比来看，本文提出的方法简便快捷，不必进行搜索迭代计算，也不必进行每次的平差计算，大大简化了粗差探测的步骤，而且定位效率也较高。

4 可靠性试验

由算例1，仅对含一个粗差的情况做如下试验。把一个粗差放在同一个位置上，用不同大小的粗差模拟出观测值。同样，每改变一次粗差大小，做1000次模拟测试计算，得到如表5所示的结果（先验中误差为±3mm）。

表5 用条件方程式直接探测多维粗差的方法探测最小粗差的能力

根据试验结果显示，随着粗差的增大，3种方法探测粗差的能力在增加，粗差探测的成功率也在提高；在探测确定接近极限误差附近的粗差值上，本文所提出的方法的探测能力更强。

5 结论和建议

1）因条件方程式的闭合差能真实反映出观测值中粗差的存在，所以用条件方程式直接探测多维粗差的方法是可行的。从基本的条件方程式计算闭合差，并运用其闭合差作为粗差的判断依据，该方法的原理简单易懂、步骤简便易实现、计算效率高、探测的准确性高、对粗差大小的灵敏度高。运用该方法进行计算，避免了反复进行平差和权阵计算，避免了反复多次迭代、搜索计算，完全可以一次计算，找出所有粗差项。

2）表2、表3说明了本方法能够准确可靠地探测粗差。和其他两方法比较说明，在相同条件下，本文提出的方法探测粗差的成功率更高。由表4证明了当观测边数增加时，也不会影响探测粗差的成功率，但随着粗差个数的增加，成功率在降低；从表5中得出，随着粗差值的增大，对这3种方法来说，成功找出粗差的几率就更大，也说明了该方法的探测接近极限误差附近的粗差的能力更强，其对粗差大小的灵敏度更高。

[1]欧吉坤.粗差的拟准检定法（QUAD法）[J].测绘学报，1999，28（1）：25-20.

[2]刘根友.粗差检定的两种途径[J].大地测量与地球动力学，2005，25（3）：29-33.

[3]Baarda W.Statistical Concepts in Geodesy[J].Neth Comm，1967，2（4）：74.

[4]李德仁，袁修孝.误差处理与可靠性理论[M].2002：236-249.

[5]范东明.测量平差模型误差的验后检验[J].西南交通大学学报，2004，39（3）：349-351.

[6]於宗俦，李明峰.多维粗差的同时定位与定值[J].武汉测绘科技大学学报，1996，21（4）：323-329.

[7]刘大杰，陶本藻.实用测量数据处理方法[M].北京：测绘出版社，2000：67-71.