全息图的小波域BP神经网络压缩实现
2014-10-25侯阿临王崇锦郭俊良
侯阿临,吴 亮,廖 庆,王崇锦,郭俊良
(长春工业大学计算机科学与工程学院,吉林长春130012)
1 引言
全息术能够展现所有视点和距离上的3D深度感知,在空间呈现真正的立体像,实现信息的三维显示,被认为是最理想的三维显示技术[1-2]。但全息图记录的信息量十分庞大,若要使全息图用于实际的通信传输和存储,高效快速的数据压缩是首先必须考虑的,因而近年来全息图的压缩成为全息领域的研究热点。传统的全息图压缩技术是用光学方法进行干涉条纹的抽除或通过研究全息图的记录、再现原理及其频谱特性,降低采样频率来实现压缩[3-4],还有如 Lucente[5]提出的面向衍射的计算全息带宽压缩理论及最近 Naughton[6-7]和 Darakis[8]等人提出的压缩方法虽然取得了一定的效果,但也存在如计算较复杂,操作步骤繁琐等问题,也有学者利用小波分析方法[9-10]进行压缩,还有运用最新的压缩传感理论提出的基于压缩传感的全息图压缩方法[11],但方法还不够成熟,算法有待优化,且计算较复杂。
由于全息图各像素间存在着很高的自相似性,且各像素分布为非线性,这种特性和神经元的联系很相似,而神经网络具有很强的学习能力,对不同的训练样本都可以产生合理的输出,这为神经网络用于全息图压缩提供了可能[12]。通过构造BP网络模型,可以减少全息图的数据冗余,实现全息图的压缩。针对全息图在输入空间是不均匀分布的,为了获取更好的网络性能和更高的压缩效率,本文提出一种全息图的小波域BP神经网络压缩算法,结合小波分析的多分辨分析特性和神经网络非线性映射和自学习能力,能够获得更好的全息图压缩效果。最后通过实验验证,本算法在保持较好的再现像质量的同时,能有效提高压缩率和运算速度。
2 全息图的小波域BP神经网络压缩
全息图的信息分布类似随机噪声的非线性分布,其各像素间的自相似性正好对应于神经网络中各神经元间的连接关系,且神经网络具有很强的鲁棒性和容错性,能提高压缩后的全息图再现质量。因此用神经网络来处理全息图比较合适,但也存在网络训练收敛速度慢,易陷入局部极小值等问题。为克服此缺点且考虑到作为训练样本的全息图的不均匀分布特点,希望在数据稠密区以高分辨率学习,而在稀疏区以低分辨率学习,用以获得更好的压缩效果,本算法将小波分析的多分辨优势应用于神经网络,既解决在不同区域以不同分辨率学习的问题,也能大大提高网络的收敛速度,使网络不易陷入局部最小值,获得更好的网络性能。且本算法具有很强的特征提取和屏蔽随机噪声能力,特别适合全息图这样非平稳、非线性信号的压缩。
根据以上思想,设计出本算法的结构图,如图1所示。压缩算法分两步完成,首先对未压缩的全息图进行小波域内的处理,然后再完成神经网络中的处理。

图1 本文算法的结构图
2.1 小波域内的处理
小波变换能把图像进行多分辨率分解,分解成不同空间、不同频率的子图像,通过对子图像的系数编码,能有效地从图像中提取高频和低频信息。在本算法中,先用小波变换对信号进行预处理,将小波基与信号的内积进行加权和来实现信号的特征提取,然后将提取的特征向量代入神经网络以完成函数逼近、分类等功能。即将待压缩的全息图经过小波变换后,再输入给BP神经网络来实现压缩。在小波域中对全息图处理步骤为:
(1)实验前制作并生成N×N像素大小的全息图及其再现像。
(2)读取并显示全息图,并对全息图进行小波的二层分解。
(3)设置全局阈值,对所有的高频系数进行同样的阈值量化处理,得到经小波变换处理后的全息图。
2.2 BP神经网络内的处理
因为隐含层的神经元个数小于输入层的神经元个数,所以输入层和隐含层的变换可看成压缩过程,隐含层和输出层的变换可看成解压缩过程。图2是BP神经网络图像压缩原理图,其中输入层输入的是原图像,隐含层就是压缩的结果,输出层是重建的图像。易知若隐含层神经元个数越少,压缩率就会越大,通过改变隐层神经元的个数,可以调整压缩率及输出图像质量。

图2 BP神经网络实现图像压缩原理图
图3是一个N-K-N的三层BP网络压缩计算模型。在模型中将输入层和隐含层间的连接权值矩阵表示成{wij∶1≤j≤K,1≤i≤N},隐含层第 j个神经元的阈值表示成{bj∶1≤j≤K};将输出层和隐含层间的连接权值矩表示成{w'ij∶1≤i≤N,1≤j≤K},输出层第i个神经元的阈值可以表示成{bi'∶1≤i≤N}。通过不断训练网络,调整网络权重,使网络的输入与输出的均方差达到最小,那么最终能将N维矢量压缩成K维矢量(K<N)。则隐含层第j个神经元的输出值为:
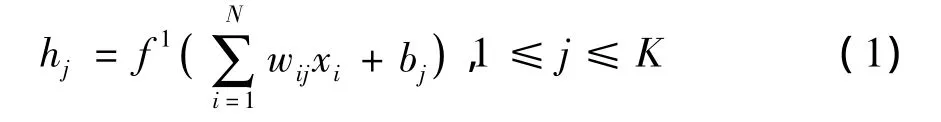
输出层的第i个神经元的输出可表示为:

其中,f1和f2分别是隐含层和输出层的激活函数;bj是隐含层第j个神经元的阈值;b'i是输出层第i个神经元的阈值。
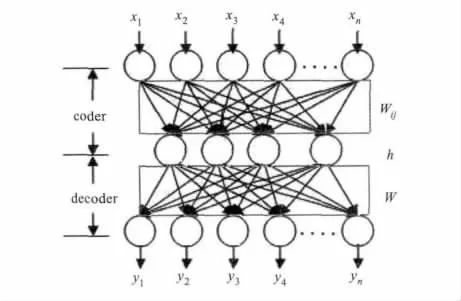
图3 BP神经网络全息图压缩模型
根据以上网络压缩原理,把已经在小波域内处理好的全息图作为训练样本,用训练好的网络对其进行压缩。具体步骤为:
(1)将经小波变换处理后的全息图分割为M个子图像块,其中每个子图像块都由P×P的子像素块构成。将每一个子图像块转换成一个P2×1维向量,P2对应输入节点个数。则全息图的数据就被划分成(N/P)2个训练向量,将其作为神经网络的训练样本。
(2)创建BP网络。通过输入层和隐含层中神经元个数比,压缩全息图。再通过隐含层和输出层中的神经元个数比,重构压缩后的全息图。
(3)对神经网络进行训练。用合适的算法训练网络,然后进行仿真实验。
(4)对仿真结果进行熵编码,重构压缩后的全息图。
(5)用菲涅尔衍射积分公式计算像平面上的光场分布,从而得到压缩后的全息图再现像。
3 实验结果与分析
在配置为Intel(R)Core(TM)i5-2450M CPU@2.50GHz 4.00GB内存的PC机上使用MATLAB R2010b对一幅256×256像素大小的图像进行仿真实验。根据全息图生成和再现原理,制作出未压缩的全息图及其再现像,如图4所示。为减少复杂性,防止神经网络规模过大,在网络训练前先对样本进行分块处理,将子图像块设为8×8像素大小,则全息图被划分成为1024个8×8的子图像块。网络的训练次数设为500次,网络目标误差设为0.001。图5则是压缩后的全息图;图6是压缩后恢复的再现像。可以看出,随着压缩比的不断增大,恢复出来的再现像清晰度不断下降,变得越来越模糊,这是因为随着压缩比的增大,隐含层神经元个数也不断减少,使得神经元之间连接关系变得简单,导致重构的全息图像素之间的自相似性降低,从而影响再现像质量。实验中可以看出,当压缩比达到 124.52∶1即0.803%的压缩率时,仍能获得像质较好的再现像。

图4 未压缩的全息图及其再现像

图5 压缩后的全息图

图6 不同压缩比下的再现像
表1是本算法与BP算法的PSNR和MSE比较,从八组对比数据看出,前三组数据表明在近似一致的压缩比下,本算法得到的峰值信噪比明显高于单纯使用BP网络的压缩算法且获得更低的均方误差。第四到第六组数据表明本算法不仅能够获得比BP算法更高的压缩比,还能获得更高的再现像峰值信噪比和更好的再现像质量。而最后两组数据则完全体现了本压缩算法的优越性,在实验中压缩比高达124.52∶1,比BP算法的压缩比几乎高出一倍,且获得了更为清晰的再现像,充分证明了对于全息图这样非平稳、非线性信号的分类压缩,本算法有着明显的优势。
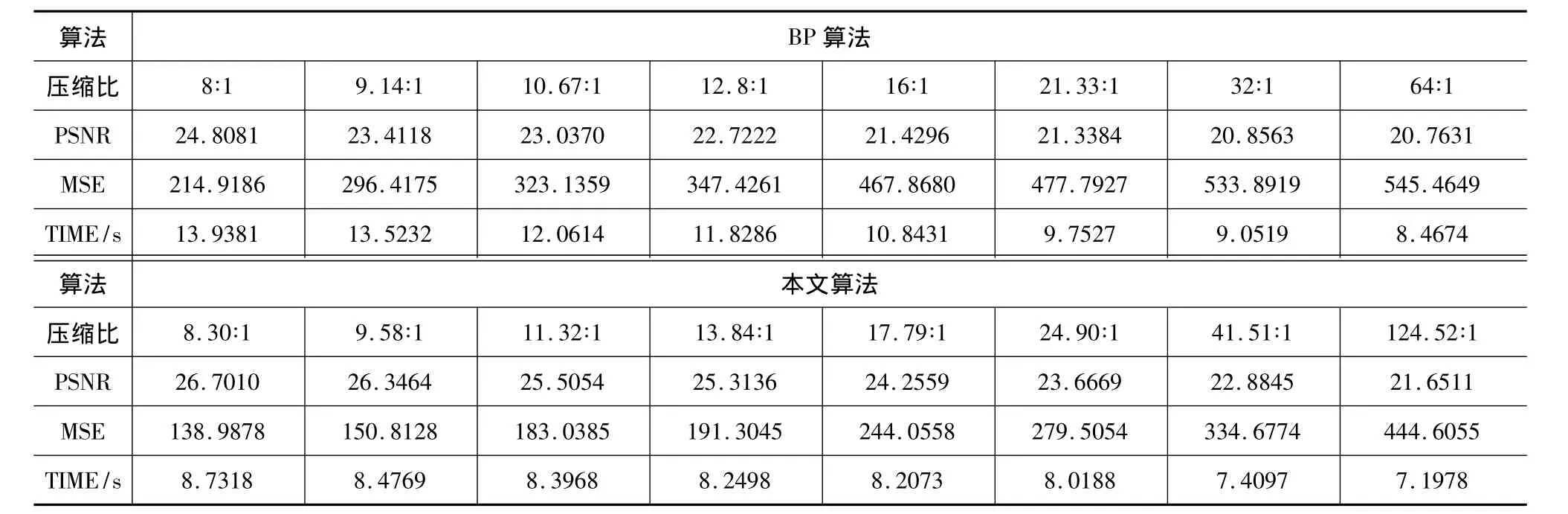
表1 本算法与BP算法的PSNR和MSE比较
从表中还可以看出不同压缩比所用的运算时间是不同的,总体变化趋势是随着压缩比的不断增加,网络运算所需的时间越少,这是因为在神经网络中压缩比不断增加导致隐含层神经元个数不断减少,使得神经元之间连接关系变得越来越简单,从而降低了网络的计算复杂度,加快了运算速度。通过数据对比发现,本算法比BP算法的网络运算速度更快,能有效节省15% ~37.35%的时间,例如在压缩比近似为8∶1时,本算法少用了5.2063 s,节省了近37.35%的时间,证明了本算法在运算速度方面表现较好,值得在后续的工作中进一步的研究和探索。
本算法将小波分析和神经网络二者各自的优势结合起来,很好地优化了网络性能,减短了训练时间,且使网络不易陷入局部最小值,从而提高全息图的压缩效率。另外,通过在小波域内进行的信号重建为网络训练提供了更加精准可靠的输入样本,使得整个网络模型具有很强的特征提取和去除随机噪声的能力,因而最终能获得更高的压缩比和更为清晰的再现像。
4 结论
本文结合小波分析和神经网络理论,提出一种基于小波域的BP神经网络压缩算法,实现了对计算全息图信息量的有效压缩,通过实验证实了该算法的可行性和有效性,且算法结构简单,计算速度快。在压缩效果方面比目前出现的一些压缩方法获得的压缩率都要高,达到124.52∶1即0.803%的压缩率,且获得更为理想的再现像质量。本研究最大的特点是为计算全息图的数据压缩提供了一个新的解决途径和研究思路,有助于解决全息图在实际传输和存储中遇到的应用问题,推进三维全息立体显示技术的快速发展。
[1] PEI Chuang,JIANG Xiaoyu,DING Sheng,et al.Three -dimensional display of computer-generated hologram based on spatial light modulator[J].Journal of Applied Optics,2013,34(5):772 -777.(in Chinese)裴闯,蒋晓瑜,丁晟,等.利用空间光调制器实现计算全息 三 维 显 示[J].应 用 光 学,2013,34(5):772-777.
[2] K Matsushima,Y Arima,S.Nakahara.Digitized holography:modern holography for 3D imaging of virtual and real objects[J].Applied Optics,2011,50(34):H278 - H284.
[3] JIN Hongzhen,LI Yong,ZHANG Haihua,et al.A method for compressing the holographic information by use of the phase information only[J].Optical Technique,2008,34(5):761 -76.(in Chinese)金洪震,李勇,张海花,等.通过保留相位进行全息图信息压缩的方法[J].光学技术,2008,34(5):761-763.
[4] LI Xu,LI Yong.A method for compressing off- axis digital hologram with spectrum shifting[J].Laser & Infrared,2008,38(8):856 -859.(in Chinese)李旭,李勇.采用移频法进行离轴全息图压缩的研究[J].激光与红外,2008,38(8):856 -859.
[5] M Lucente.Computational holographic bandwidth compression[J].IBM System Journal,1996,35(3&4):349-365.
[6] T J Naughton,J B McDonald,B Javidi.Efficient compression of Fresnel fields for internet transmission of threedimensional images[J].Applied Optics,2003,42(8):4758-4764.
[7] T J Naughton,Y Frauel,B Javidi,et al.Compression of digital holograms for three-dimensional object recognition[J].Appl.Opt.,2002,41:4124 -4132.
[8] Darakis E,Naughton T J,Soraghan J J.Compression defects in different reconstructions from phase-shifting digital holographic data[J].Applied Optics,2007,46:4579-4586
[9] CAI Xiaoou,WANG Hui,LI Yong,et al.Hologram compression by wavelet analysis[J].Acta Photonica Sinica,2000,29(8):738 -743.(in Chinese)蔡晓鸥,王辉,李勇,等.全息图压缩的小波分析方法[J].光子学报,2000,29(8):738 -743.
[10] HAN Pengfei.Preliminary investigations on information compression of holograms[D].Harbin:Harbin Institute of Technology,2007.(in Chinese)韩鹏飞.全息图信息压缩的初步研究[D].哈尔滨:哈尔滨工业大学,2007.
[11] LI Ke,LI Jun.Hologram Compression Based on Compressive Sensing[J].Journal of South China Normal University:Natural Science Edition,2012,44(4):61 - 65.(in Chinese)李科,李军.基于压缩传感的全息图压缩研究[J].华南师范大学学报:自然科学版,2012,44(4):61-65.
[12] HOU ALin,LIAO Qing,JIN Zhi- Juan,et al.Research on compression of computer-generated hologram based on artificial neural network[J].Journal of Jilin University:Engineering and Technology Edition,2013,43(Sup.):21-24.(in Chinese)侯阿临,廖庆,靳志娟,等.计算全息图的人工神经网络压缩算法[J].吉林大学学报:工学版,2013,43(Sup.):21 -24.
