疲劳试验下应力集中与磁信号的关系

方发胜，周 培，张利明，饶 琪，任吉林

（1.杭州华安无损检测技术有限公司，杭州 310023；2.上海飞机制造有限公司，上海 200436；3.南昌航空大学 无损检测技术教育部重点实验室，南昌 330063）

疲劳断裂失效是构件失效的主要形式（占80%以上），主要由应力集中引起的微观和宏观缺陷、疲劳累积损伤所导致［1－2］。由于疲劳裂纹一般萌生于近表面、表面缺陷产生的应力集中部位，应力集中还会导致某些构件出现一些应力腐蚀等早期损伤，因此，对铁磁构件应力集中位置以及应力集中程度的检测，以及对构件损伤的早期诊断显得很重要。近年来兴起的磁记忆检测技术，立足于评价铁磁性金属构件的应力集中部位及应力集中程度，对于应力集中部位缺陷的产生有预报作用，在铁磁构件的评价以及早期损伤诊断方面具有很大的潜力，能够准确地检测出铁磁性金属构件的危险部位，是对铁磁构件疲劳断裂早期诊断，预防危险事故发生的目前最为有效的方法［3－4］。但因为磁记忆检测技术的影响因素较多，目前，不仅利用单一的磁记忆法向特征参量进行评估的可靠性不高，容易出现漏检误判等不足；而且在磁记忆检测定量的分析上也没有取得突破性进展。

笔者通过对40Cr试件进行高周疲劳试验，研究了疲劳试验过程中磁信号的特征值与应力集中位置及应力集中程度的关系，并联合法向分量、切向分量磁信号进行二维检测［5－6］；引入李萨如图［7］分析法，探索了李萨如图面积与疲劳损伤之间的关系，改变了以往利用单一磁记忆法向信号作为铁磁性构件疲劳早期损伤判据的情况。

1 试件选择

选用优质合金钢40Cr进行疲劳试验。40Cr钢硬度、强度良好，同时具有很好的抗疲劳能力，因此使用该材质的试件便于在整个疲劳试验过程中观察和提取磁信号。40Cr钢材料主要成份为：C 0.37%；Si 0.27%；Mn 0.80%；S 0.03%。其性能参数σs为805MPa；σb为915MPa；E 为211GPa。试验试件尺寸设计如图1所示。试件经过850℃～890℃淬火，然后500℃～520℃回火，最后油冷的热处理工艺。为了消除热处理以及试样加工等外界因素对残余应力的影响，疲劳试验开始前需对试件去应力退火处理。

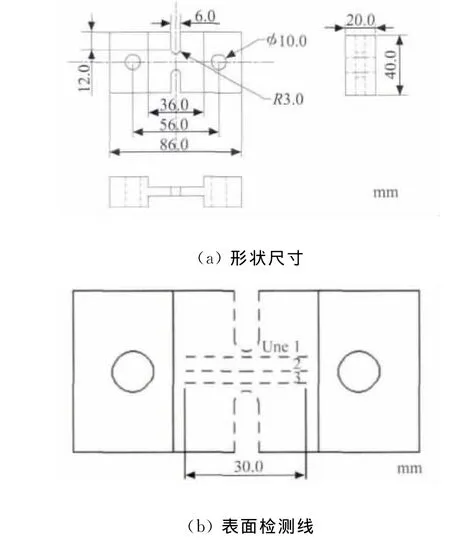
图1 40Cr试件的尺寸形状及测量线

2 试验过程

2.1 试验设备

（1）QBG－100型高频疲劳试验机，如图2所示。高频疲劳试验机主要用于对试件进行室温状态下的拉伸、压缩或拉压交变负荷的疲劳特性、疲劳寿命、预制裂纹及裂纹扩展试验。根据40Cr试样的力学性能，同时考虑到试件疲劳时间长，疲劳过程中会出现发热现象影响试验结果，选用疲劳应力水平为：静载荷18kN＋动载荷12kN，参数应力比为0.2。

图2 高频疲劳试验机和装载试件图

（2）采用两台美国LakeShore公司生产的，适用于弱磁信号测量的LakeShore 421型高斯计（图3）进行磁信号的测量。LakeShore 421型高斯计分辨率较高，可以精确地测量试样表面磁信号。

（3）采用实验室自制的二维磁记忆测量系统（图4）进行磁记忆数据的采集，该系统由高斯计、计算机、步进电机扫描系统及驱动电路组成。试验通过磁记忆测量系统对试件表面磁记忆法向、切向信号进行实时采集和保存，并通过相应的数据处理方式实时显示扫描结果。

图3 421型高斯计

图4 二维磁记忆测量系统

2.2 试验步骤

2.2.1 试验前阶段

试验选用疲劳应力水平为：静载荷18kN＋动载荷12kN，参数应力比为0.2。疲劳应力是正弦波形，加载频率f为130Hz。根据金属构件断裂失效理论以及试样形状可以判断，试件U型口根部横截面最窄的区域是应力集中区，此处将会出现裂纹，发生断裂，因此在探讨40Cr试件应力集中与磁信号规律时，在横切面最窄部位以及附近范围内设置了三条测量线。为了准确地提取整个疲劳过程中试件表面法向、切向磁信号的变化情况，采用加载一定循环周次后，对试件进行卸载离线测量的方法。测量过程中，利用实验室自制的二维检测扫描系统，分别对测量线1～3号进行磁记忆信号采集，然后对得到的磁信号进行处理分析。

2.2.2 磁信号测试阶段

将二维检测系统中的探头按照计算机中预先设定的路径和间距对试件进行扫查；使用一台高斯计，利用轴向探头提取磁记忆法向分量磁信号Hp（y）；运用矢量合成原理，使用两台高斯计，利用两个横向探头相互垂直的方法提取切向分量Hp（x）最大值；然后经过软件显示存储模块实时显示采集到的数据以及曲线图形，保存数据。

3 试验结果分析

3.1 应力集中程度与磁信号的关系

应力集中是指试件上存在的几何不连续点导致应力分布不均，而不连续点附近范围内的应力明显高于其它地方应力的现象。它一般出现在物体形状突变的部位，然而应力集中部位最容易产生疲劳以及静载断裂，因此对应力集中部位以及程度的探讨显得尤其重要。通常用最大应力值与基准应力值的比值反映应力集中程度。在基准应力值固定的条件下，应力集中程度由最大应力值的大小决定。在疲劳循环到同一循环次数时，疲劳试件不同位置处因为几何形状不同导致分布的应力大小也不一样，而不同的应力大小意味着不同的应力集中程度。针对试验选用的含双侧U型缺口的40Cr试件，应力最大值出现在靠近U型缺口的部位，即此处应力集中程度最大，远离U型缺口，应力值变小，应力集中程度也相应变小。同时，一般情况下，同一位置处的应力值随着疲劳循环次数的增大而增大，应力集中程度也相应增大。

根据金属构件断裂失效理论及试样形状分析可知，试件表面的1号与3号测量线的磁信号变化规律相似。疲劳条件下，检测试件的应力值最大值出现在1、3号测量线的中心位置分别与各侧的U型缺口垂直相交的部位，而2号测量线的中心位置与U型口垂直相交的部位应力值不及最大应力值，但也相对较大，而远离U型缺口部位的应力值则较小。现通过分析比较1～3号测量线的磁信号曲线，来研究40Cr试件应力集中与磁信号之间的变化规律。图5为疲劳加载前以及整个疲劳过程中1、2号测量线上磁记忆法向分量信号Hp（y）的分布曲线，图中N后数字表示循环周次数，以下同。

由于试样形状和疲劳加载应力的对称性，1、3号测量线磁信号有相同的变化规律，从图5可以发现，疲劳加载前，试件的残余应力均匀分布，试件上各测量线上的法向磁信号很小，并且变化平缓，法向分量曲线没有出现过零现象。当加载疲劳应力后，各测量线的磁记忆法向分量都发生明显改变，出现过零现象。加载后2号测量线比1号测量线磁信号小，同时2号测量线上的磁信号比1号测量线上的磁信号变化平缓，即在试件的同一检测平面上，离U型缺口位置较近的1、3号测量线检测位置处应力集中程度大于离U型缺口位置相对较远的2号测量线检测位置的应力集中程度，并且，1、3号测量线上的磁信号变化比2号测量线上的更明显。

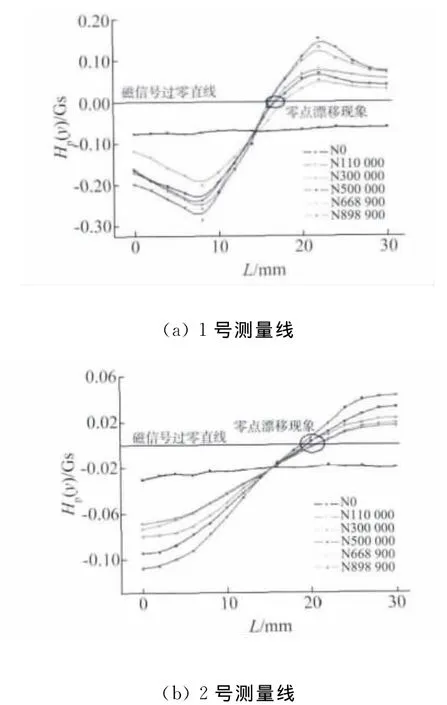
图5 不同循环周次下1、2号测量线的法向分量磁信号

同时可看到，40Cr的高周疲劳试验在测表面法向磁信号时，加载时开始，磁信号显著增加，然后随着加载循环次数增加磁信号缓慢增加，到中间阶段，随着循环次数的增加磁信号减小，最后在裂纹萌生阶段磁信号急剧增加。即在断裂前最后一次测量89.89万次时，1、2号检测线上的磁信号都急剧增加。

3.2 应力集中位置与磁信号的关系

同样通过图5分析静载荷18kN＋动载荷12kN作用下，不同疲劳循环次数下磁信号的变化与应力集中位置之间的关系。由图5可见，疲劳试验过程中，法向分量磁信号存在零点漂移现象，两测量线上的磁信号过零点都与试件断裂位置不在一起，试件断裂位置在图中显示是15mm处，而图5中磁信号过零点与试件断裂位置存在一定程度的偏离，这一现象在应力集中程度较小的2号测量线上更为明显。通过对不同疲劳循环周次下法向分量磁信号Hp（y）曲线的过零点位置的变化进行分析，发现随着试件疲劳循环周次的增加，损伤程度增加，法向分量磁信号Hp（y）的过零点有向试件断裂处逐渐靠近的趋势。由此得知，疲劳损伤程度越深，法向分量磁信号Hp（y）的过零点所在的位置就越能准确地表征反映试件疲劳损伤断裂位置。

为了消除初始磁场对疲劳加载过程中测量的磁信号的影响，选用应力集中程度较大的1号测量线上的法向与切向分量减去初始信号后的磁信号进行分析，发现用疲劳循环过程中1号测量线上的法向分量、切向分量磁信号减去它们的初始磁信号后，磁信号过零点与试件断裂位置基本符合，偏离距离很小，如图6所示。因此，该方法可以更准确地判断应力集中位置。

从图6发现，40Cr试件在疲劳加载循环条件下，法向磁信号出现过零现象，切向信号出现最大值，在裂纹萌生阶段，法向与切向分量磁信号都急剧增加，而法向分量磁信号比切向分量磁信号值变化大。

然而，从漏磁检测中的磁偶极子模型中切向和法向磁场计算方法中，发现磁信号反应的是应力集中区的自由漏磁场的积分场，考虑到法向与切向分量磁信号微分后的梯度值绘制的李萨如图能够为磁记忆二维检测定量化提供试验依据，并且微分后的梯度值能够更准确地符合漏磁场法向与切向分量磁信号分布特征，因此采用微分法，分别对应力集中程度较大的1号测量线法向切向分量的磁信号进行微分，得到试件各检测点自有漏磁场微分后的曲线，如图7。

图7 法向与切向分量微分后的曲线

图7（a）是在静载荷18kN＋动载荷12kN的疲劳应力条件下，应力集中最大的1号测量线上的法向分量磁信号微分后的梯度K分布曲线，图7（b）是同样条件下1号测量线上的切向分量磁信号微分后的梯度K分布曲线。由图7可见，磁信号法向、切向梯度K曲线分别出现异变点峰值和过零点现象。异变点和过零点位置准确反映了试件疲劳损伤的位置。1号测量线法向分量磁信号微分后的梯度K曲线存在两个异变点，在两个异变点之间即试件U型缺口顶点的位置存在最大梯度值Kmax，切向分量磁信号微分后的梯度K曲线在试件U型缺口附近存在2个异变峰值（Kmax），并且在U型缺口顶点的位置出现过零现象。由此可知，与未经过微分处理的磁信号相比，微分后的法向梯度K曲线中最大梯度值Kmax的位置以及微分后的切向分量梯度K曲线中过零点的位置，能更准确地反映出试件疲劳损伤位置，并且得出法向微分K曲线、切向微分K曲线异变点之间的距离与试件U型缺口及其附近应力集中分布的区域存在着对应关系。

3.3 李萨如图面积与疲劳损伤程度的关系

为了定量分析疲劳循环过程中，磁信号变化与疲劳损伤程度之间的对应关系，利用二维检测的方法，将法向和切向分量的磁信号微分后的梯度值联合绘制成稳定封闭的李萨如图，利用李萨如图面积的大小对应力集中程度进行衡量。

图8是1号测量线上法向和切向分量磁信号微分后的梯度K曲线合成的李萨如图，图形封闭区域面积的变化情况与试验过程中测得的法向与切向分量磁信号变化情况一致，同时发现，在疲劳试件循环了105周次以上时，李萨如图的面积变化不大，而是出现一个相对稳定的状态，表明试件处于稳定循环阶段；而当疲劳试件循环至8.9×105周次时，试件出现裂纹萌生现象，此时的李萨如图形面积显著增加。李萨如图在稳定循环阶段的面积变化不大，保持基本一致；而当试件出现裂纹萌生现象后，李萨如图面积明显比稳定循环阶段的大，此规律表明磁记忆检测中，法向与切向分量磁信号微分后的梯度K曲线合成的李萨如图面积与试件的疲劳损伤状态之间存在良好的对应关系。

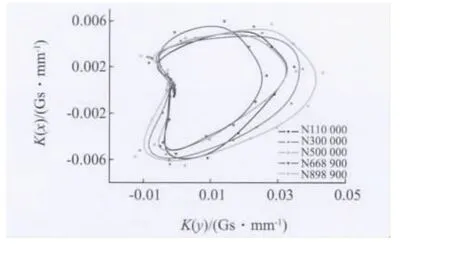
图8 法向切向梯度值合成的李萨如图

3.4 李萨如图面积的求解

大量试验表明，李萨如图封闭区域面积大小可以衡量应力集中程度。通过计算李萨如图的面积，并与构件受载情况进行对比分析发现，面积大小的变化情况以及具体的面积值可以反映出试件所处的阶段，因此李萨如图面积的确定显得尤其关键。

由于李萨如图为不规则图形，为了能快速精确地算出应力集中部位李萨如图封闭区域的面积，可采用opencv的内置函数算法来直接求取李萨如图形轮廓所包围的面积大小，求得如图9所示的李萨如图形面积为1.222 75Gs2／mm2。

Opencv内置函数得出轮廓内的像素点总数，再运用到格林公式，从而算出李萨如图形的封闭区域面积：

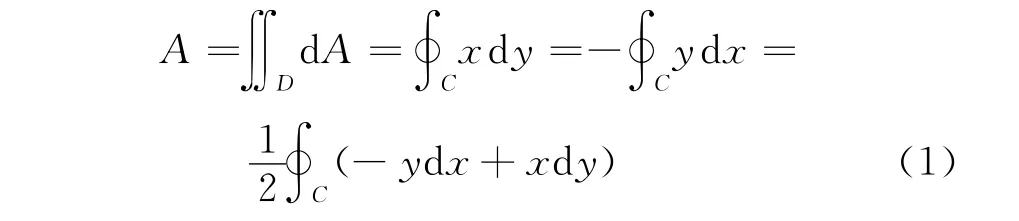
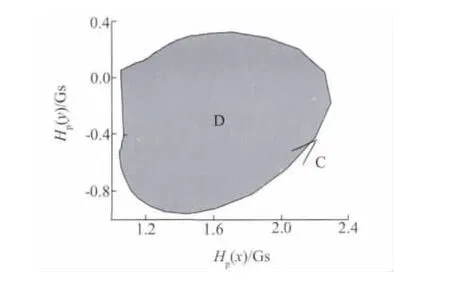
图9 opencv面积求解示意图

另外一种计算李萨如图面积的方法为网格法，其通过运用在李萨如图封闭区域范围内划分网格的方法可计算出李萨如图封闭区域面积值，如图10所示。图中横纵坐标均为磁场强度值，单位为A／m，将其转为磁感应强度值，单位为Gauss，其中1 Gauss≈80A／m。此种方法可以通过调整网格大小进行计算精度的调节。

图10 网格面积法示意图

对图8中不同应力下稳定封闭的李萨如图面积进行运算，得出李萨如图面积值，加载循环次数分别为110 000，300 000，500 000，668 900，898 900时，对应的面积为 0.000 28，0.000 31，0.000 25，0.000 21，0.000 47Gs2／mm2。

从数值可以看出，李萨如图的面积大小直观地反应了疲劳加载循环不同阶段的磁信号的变化。从李萨如图的面积得到，40Cr材料在一受到疲劳应力时，磁信号便开始显著增加；在随后的疲劳循环阶段，磁信号相对保持稳定，面积值变化不大；当试件出现裂纹萌生现象时，面积值相对显著增加，此时试件处于危险阶段。即磁记忆检测中，法向分量和切向分量磁信号微分后的梯度K曲线合成的李萨如图面积与试件的疲劳损伤状态之间存在良好的对应关系。

4 结论

通过对40Cr材料进行高周疲劳试验，研究了疲劳试验过程中磁信号的特征值与应力集中位置及应力集中程度的关系，并联合法向分量、切向分量磁信号进行二维检测，引入李萨如图分析法，探索了李萨如图面积与疲劳损伤之间的关系，得出以下结论：

（1）疲劳循环加载条件下，磁信号在疲劳加载开始阶段出现相对较大变化；随着疲劳循环次数的增加，磁信号变化缓慢；当试件进入裂纹萌生阶段时，磁信号显著增加，此时试件处于非常危险的阶段。

（2）对疲劳条件下检测的磁信号法、切向分量求微分，磁信号法、切向梯度K曲线分别出现异变峰值和过零点现象。利用微分后的梯度值突变特征，可准确确定试件疲劳损伤引起的应力集中部位。

（3）将法向、切向磁信号联合利用，引入李萨如图分析法。微分后的磁信号梯度值合成的李萨如图面积可以准确直观反应应力集中程度，即可利用李萨如图面积反映试件的疲劳损伤状态。

综上所述，通过对疲劳试验过程中磁信号的研究，探讨了磁信号与应力集中程度与应力集中位置的关系，同时为磁记忆二维检测定量分析的研究提供可靠的试验依据。

［1］ 苏兰海，马祥华，陈工，等.铁磁材料零件疲劳损伤磁记忆检测方法的实验［J］.测试技术学报，2009，23（2）：145－150.

［2］ 刘昌奎，陈星，张兵，等.构件低周疲劳损伤的金属磁记忆检测试验研究［J］.航空材料学报，2010，30（1）：72－78.

［3］ DOUBOV A A.Diagnostics of metal items and equipment by means of metal magnetic memory proc of CHSNDT［C］／／7th Conference on NDT and International Research Symposium Shantou，China，1999：181－187.

［4］ 任吉林，林俊明，任文坚，等.金属磁记忆检测技术研究现状与发展前景［J］.无损检测，2012，34（4）：154－159.

［5］ 任吉林，王进.一种磁记忆检测定量分析的新方法［J］.仪器仪表学报，2010，31（2）：431－436.

［6］ 任吉林，周培，陈曦，等.磁记忆切向分量信号的检测试验［J］.无损检测，2011，33（12）：1－5.

［7］ 杨继先.李萨如图形的性质研究［J］.西华大学学报，2008，27（6）：98－100.