电子负载补偿电路设计

袁 博，黄 亮，全书海

（武汉理工大学自动化学院，湖北 武汉 430070）

低功率瓷盘电阻、滑线变阻器或电阻箱常作为测试负载，这些负载分辨率低，阻值会因接触不良和发热发生变化，并且它们大都设备笨重，携带不便，调节费力，精度难以保证。负载电流不能连续调节，在加电的状态下从零调到满载，易接触不良，打火烧毁，难以用于程控化、数字化的自动化生产线上，更不能测试电源的动态参数［1］。针对大量场合需使用负载对产品进行测试，而现有负载不能实现平滑调节的问题，采用功率场效应晶体管（MOSFET），靠控制功率管导通量改变功率管耗散功率的电子负载已成为研究的热点。

文献［2］中提出了一种电子负载的拓扑，该拓扑工作时能将一部分电能储存在电池中，但是该结构响应速度不快，该结构远远不能满足一些高速测量的要求。文献［3］给出了电子负载的拓扑，并对电子负载进行了大致的分析，没有详细分析电子负载结构。文献［4－6］介绍了电子负载的控制与工作原理，加入了数字控制环节，在一定程度上提高了电子负载的精度，但是并未给出电子负载的详细模型，仅通过控制算法的改进提升电子负载的性能。文献［7］提出了能馈电子负载，但是对电子负载响应速度没有进行分析。文献［8］分析了电子负载的模型，该模型基于电子负载外部等效模型，设计了不同的控制环路，但是该模型未能详细描述电子负载内部结构，且响应速度不快。

笔者通过加入驱动增强电路提高了电子负载响应速度，建立了电子负载的模型并绘制电子负载开环伯德图，利用补偿电路对电子负载进行补偿，并对该电路进行了改进，使其超调量减少，实现无静差响应，保证了电子负载模拟闭环控制的快速性，并通过实验验证了该补偿器的稳定性。

1 电子负载工作方式及模型

1.1 电子负载工作原理

如图1所示，电子负载的结构以MOS管为主，被测电源的电能主要消耗在MOS管上。当MOS管源极和漏极两端存在正向电压时，MOS管上有电流流过，这时MOS管上会有功率消耗。由于栅源电压的大小决定流过MOS管最大电流的大小，因此，在MOS管上消耗的功率是可以控制的。电子负载在工作时通过采样电阻上的电压与给定电压和运算放大器共同构成负反馈，运算放大器为MOS管提供偏置电压，改变MOS管流过电流的大小，从而达到动态平衡。

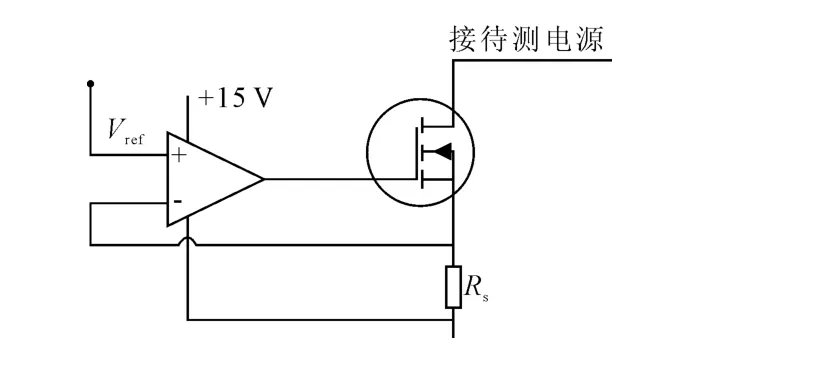
图1 电子负载原理图

1.2 提高电子负载驱动能力

对于实际的运算放大器，输出功率不足会引起整个电子负载响应速度减慢以及输出振荡，因此在运算放大器输出端加入晶体管的发射极跟随器就可以起到增大电流的作用。

如图2所示，加入晶体管电路后运算放大器的驱动能力有所增强，电阻R1、R2和R3能够使运算放大器直接提供两个晶体管不灵敏区的电流，填埋由两个晶体管出现的1.4 V不灵敏区［9］。

图2 增强运算放大器驱动能力的电路图

1.3 电子负载模型

由于电子负载中MOS管工作在饱和区，其传递函数随负载的变化而变化。对于电子负载本身而言，其内部模型不易求出，可通过测量得出。利用PSpice绘制电子负载伯德图进行分析，并确定补偿网络的参数。首先，在PSpice中绘制电子负载原理图，在给定信号处加入一定的直流偏置，该直流偏置决定了电子负载消耗功率的大小，并保证了电子负载工作在正常的工作范围内，接着叠加一个频率变化的输入给定，采样电阻上的电压即为输出。当输入量的幅值为1时，输出即为系统的传递函数。

如图3所示，在给定信号处加入输入幅值为1的频率变化的正弦波信号于一定的直流偏置电压上，不断调节输入的频率值，测量电阻R上电压的幅值和相位就可以绘制电子负载开环传递函数的伯德图。

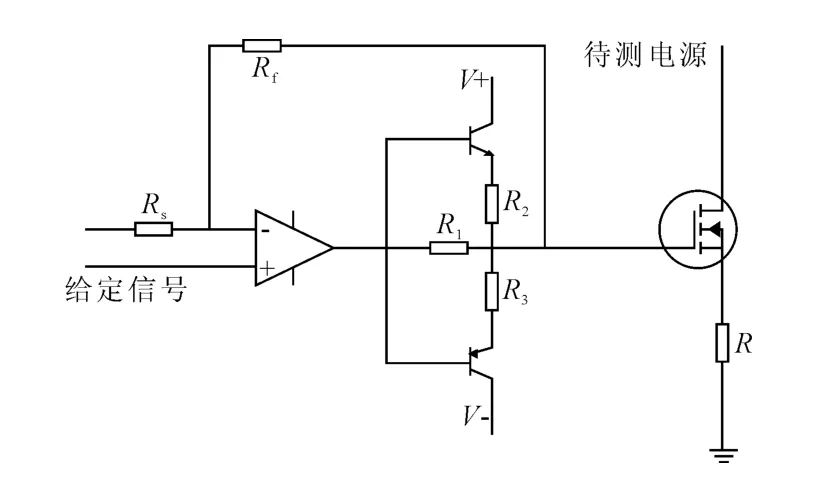
图3 提高运算放大器输出能力的电子负载图

理想运算放大器是一个增益无穷大，带宽无穷宽的放大器，而实际中运算放大器有固定的带宽和增益，当输入超过运算放大器的设计时，输出会出现失真。如图4所示，其中实线部分是使用理想运算放大器绘制的伯德图，可以看出理想的运算放大器使系统在全频带内稳定，并且有很宽的相位裕度。实际的运算放大器由于带宽和增益的限制，在较低的频率处经过0 dB，并且相位裕度很小。如果考虑到直流母线上的分布电感，则整个系统没有充足的相位裕度，整个系统在开环时是不稳定的。

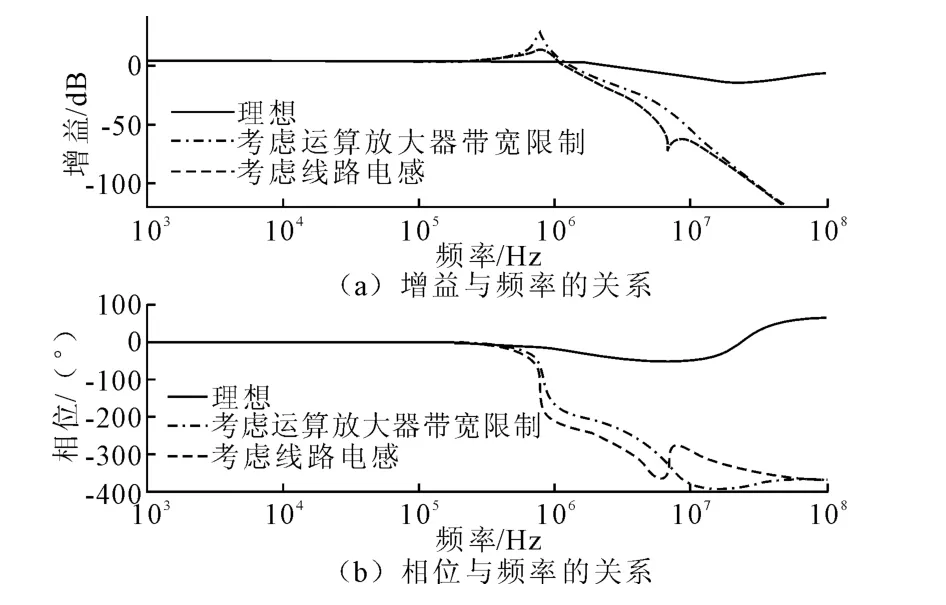
图4 考虑实际因素的电子负载伯德图

直流母线上的分布电感是不可消除的，但是可通过设计工艺减少，该电感不会有一个确切的值，以下内容忽略分布电感对系统产生的影响。分别调节电子负载偏置电压的大小就能得到电子负载在不同负载下的伯德图，图5中分别表示了负载电流为500 mA和2 A时电子负载开环伯德图。可以看出电子负载在轻载和重载时的伯德图大体趋势相同，但是电子负载的零极点随负载变化而变化。负载重时，极点频率低。重载时系统的截止频率在 fc=1.2647 MHz，相位裕度为－5.302，直流增益为 3.58 dB，Q=10.17 dB。轻载时系统截止频率在fc=1.8239 MHz，相位裕度为 －26.171，直流增益为 1.83 dB，Q=16.63 dB。

2 电子负载补偿网络的设计与改进

2.1 单极点补偿

补偿网络是在系统中利用其输入或反馈网络来改变运算放大器相应的阻抗参数和校正系数的动态指标。它的主要作用是在适当的频率处提供超前或滞后的相位，并且使系统的开环频率特性在较高频率处穿越0 dB线，从而获得较宽的频带，使系统快速响应［10］。

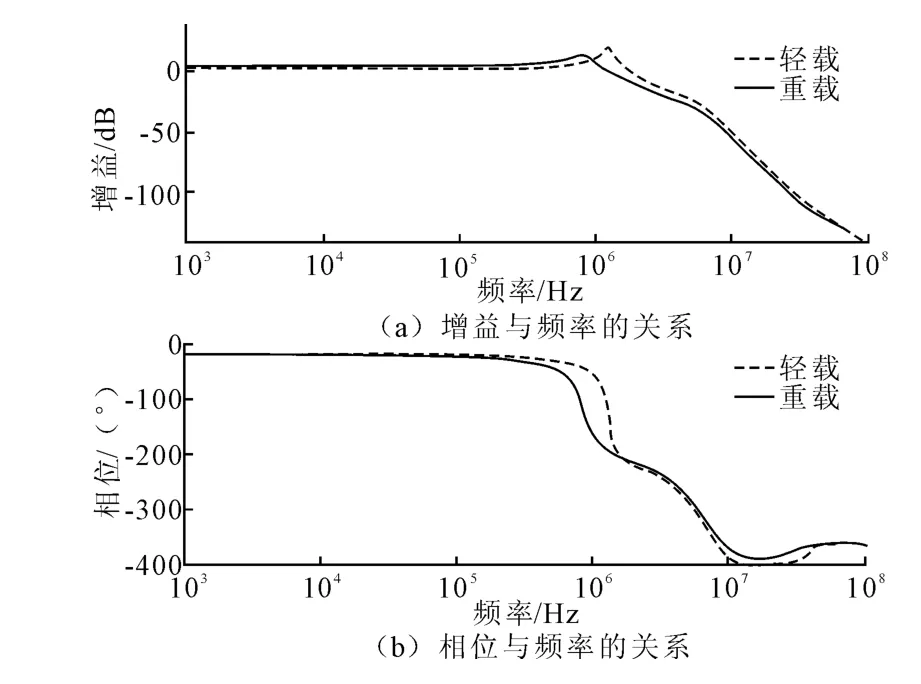
图5 不同负载下的电子负载伯德图

图6为单极点补偿电路，其传递函数如式（1）所示:

MS，之前又被称作MSP（maritime services portfolio，海事服务集），自2018年10月末在伦敦IMO总部召开的HGDM 2次会讨论之后，更名为MS，其定义为“具有协调统一格式的海上相关信息及数据的供应和交换（HGDM 2/10 4.1.1）”。最新定义大大拓展了MS可能涉及的领域，一切与海上信息相关的服务，都有可能成为一种MS。而目前，MS已确定的服务有16种。如表1所示。

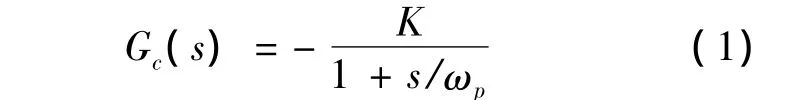
式中:极点角频率ωp=1/（R2C）；直流增益K=R2/R1。

图6 单极点补偿电路图

考虑实际运算放大器的增益限制以及带宽限制，并且保证系统在工作时有足够的相位裕度及增益以－20 dB/十倍频过零，设计经过补偿后系统截止频率为100 kHz，极点的频率设计为fp=100 Hz，直流增益为 60 dB。则 K=1000，ωp=2πfp=628 rad/s。取 R1=1 kΩ，则 R2=1 MΩ，C=1.6 nF。

如图7所示，加入补偿网络后系统的截止频率由1.26MHz变为154kHz，并且有较大的相位裕度，实现了系统闭环稳定。通过对负载施加阶跃输入可以观测系统的阶跃响应。

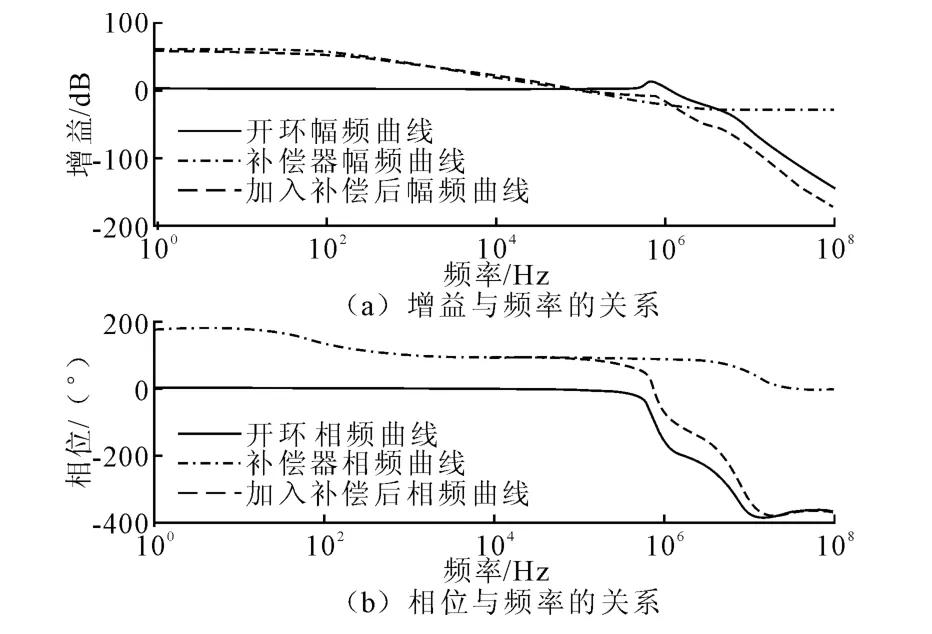
图7 单极点补偿系统伯德图

如图8所示，电子负载在该调节器下响应速度较快，基本吻合响应曲线，但是出现了较大的超调。这种系统的补偿有自身的缺陷，系统在低频环节可以近似为一个0型系统，虽然直流增益大，系统中出现的误差难以看出，但是该补偿器的静差依然存在。

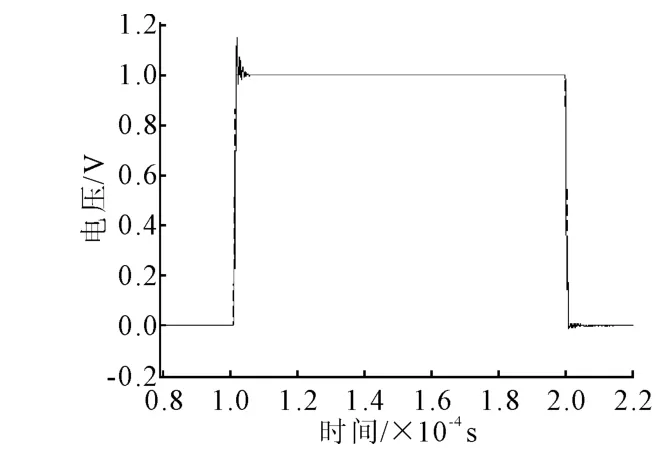
图8 单极点补偿系统响应图

解决上述问题的最优方法是在系统低频环节加入积分环节，这样能消除静差，减小系统超调。

2.2 单极点单零点补偿图

图9所示为在原有补偿器基础上加入了一个电容C1，这个电容分别在传递函数中加入了一个零点和一个极点的补偿电路，该传递函数可写为:

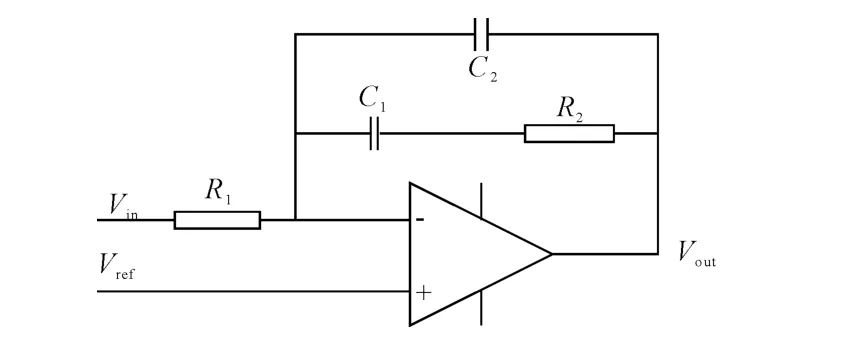
图9 单极点单零点补偿电路图

加入补偿器后系统截止频率为fc=116 kHz，相位裕度为45°，满足设计需求。补偿后，就低频特性而言是一个I型系统，其稳态误差等于零。该系统的阶跃响应如图11所示。

可以看出，将补偿器进行改进后系统对响应的超调量减小，响应速度与补偿器改进前相当，能够无静差地对系统进行调节。

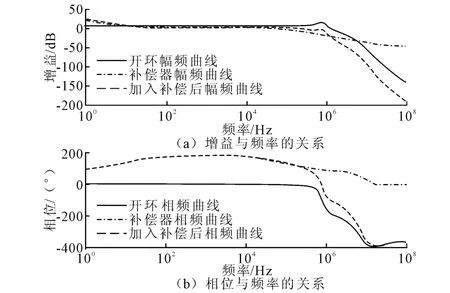
图10 单极点单零点补偿系统伯德图

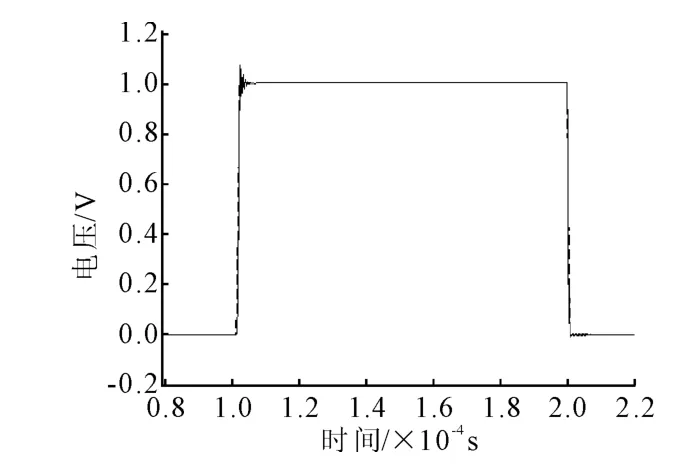
图11 单极点单零点补偿系统响应图

3 实验分析

通过实验可以对上述补偿器补偿后的系统响应速度进行验证。实验中选用IRFP260N作为实验用功率MOS管，LM358作为驱动运算放大器，LF412作为补偿器控制运算放大器，采样电阻为0.5 Ω，当电子负载输入电流为1 A时，测量的峰值应为500 mV。实验中分别对单极点补偿器和单极点单零点补偿器进行验证，测量响应速度和超调量。

如图12所示，对于单极点补偿器系统，系统超调量接近20%，并且与给定存在静差，不能较好地跟随输入响应。图12中下方波形为给定，上方波形为响应。

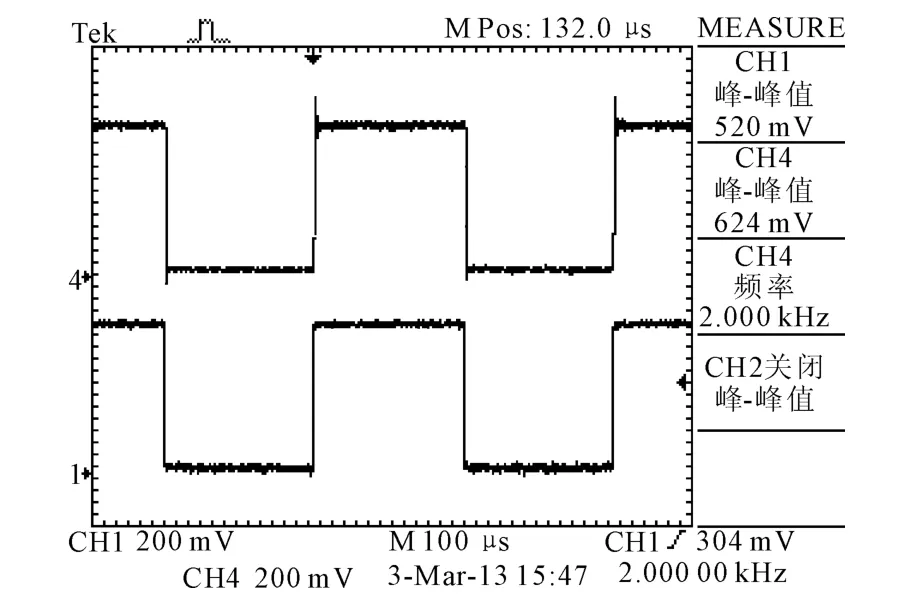
图12 补偿器改进前系统响应界面图

补偿器改进后系统响应界面图如图13所示，在相同输入给定情况下，系统超调量减小，响应速度略有提高，且响应过程没有静差，满足了系统的要求。实验中的波形和数据与仿真结果相似，更进一步地验证了该误差调节器的可行性。

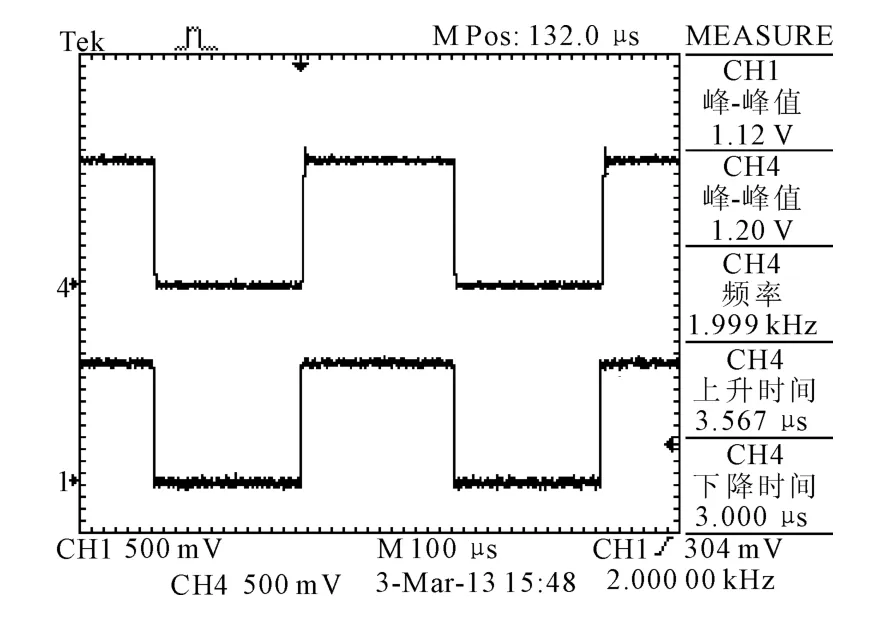
图13 补偿器改进后系统响应界面图

受线路电感以及元件分布参数的影响，电子负载在更高频率下会出现响应速度变缓的情况。

4 结论

传统电子负载大都以数控为主，通过数字控制调节电子负载响应速度，而没能对模拟补偿引起足够重视。笔者通过对电子负载驱动电路设计，提高了电子负载的响应速度，在此基础上绘制电子负载伯德图，找出实际中引起电子负载开环输出振荡的原因，加入了模拟补偿电路，在保证系统带宽的同时，使开环传递函数以－20 dB/十倍频经过0 dB并且有充足的相位裕度。在调节器设计上，由单零点补偿电路变为单极点单零点的补偿电路后更能减少响应的超调量，提高电子负载的性能。

［1］李卫华，谢珩.关于电子模拟负载研究现状的探讨［J］.新余高专学报，2005，10（2）:47 －49.

［2］TSAN K M，CHAN W L.Fast acting regenerative DC electronic load based on a SEPIC converter［J］.Power Electronics，2012，27（1）:269 －275.

［3］MANTINGH E G.Ultimate transistor electronic load for electrical performance measurement of photovoltaic devices using pulsed solar simulators［C］∥IEEE Photovoltaic Specialists Conference.［S.l.］:［s.n.］，1994:871－873.

［4］王子剑，孔峰.基于DSP的数字电子负载控制器设计［J］.计算机技术与发展，2010，20（2）:241 －244.

［5］高嘉英，高玉峰，刘亚龙.基于新型电子负载恒流放电设备的研究［J］.电源技术应用，2007，10（8）:48 －51.

［6］吴文进，江善和.多功能直流电子负载的设计与实现［J］.安庆师范学院学报:自然科学版，2011，17（3）:42－45.

［7］陈强，鞠文耀，贾中璐.电能回馈直流电子负载的设计与实现［J］.电力电子技术，2011，45（7）:108 －110.

［8］YASUHIKO M，TAKAHIDE S，ETSUNAO O.Constant voltage control of electronic load using robust digital controller［C］∥ICCAS － SICE.［S.l.］:［s.n.］，2009:4579－4582.

［9］冈村迪夫.OP放大电路设计［M］.北京:科学出版社，2004:140－142.

［10］张卫平.开关变换器的建模与控制［M］.北京:中国电力出版社，2008:140－141.