一种改进的移动机器人自定位算法

张 琪，蒙禾青，周 嵘，包琨超，王宗玉

（1.武汉理工大学 信息工程学院，湖北 武汉 430070；2.西安交通大学软件学院，陕西 西安 710049）

自定位是移动机器人的核心问题。通过自定位，移动机器人可以在特定环境中完成人类指定的各种任务，例如传递指令、取送物品、危险物排除、管理办公室或家居和机器人足球等［1－2］，因此这项研究具有重要价值。移动机器人的定位，需要两个条件:一是感知内、外环境的传感器，例如笔者采用经典的测距传感器来获取环境信息；二是关于行走环境的地图。地图的获取有两种方式，一是机器人在行走过程中根据实际量测来自动绘制环境地图；二是把已经标定好的环境地图存放在移动机器人的芯片中。为了简化问题，笔者采用第二种方式，即地图在自定位之前已经获得。地图采用离散栅格形式，如图1所示。其中黑色栅格表示障碍物，用数字0表示，而白色部分表示机器人可以通过的栅格，用数字1表示。

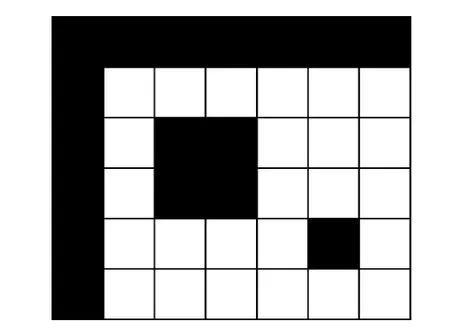
图1 离散栅格地图示例

地图建立以后，机器人通过移动，不断获取与墙壁或周边物体的距离信息，经过与地图的匹配，逐步判断机器人在当前时刻的位置和方向。由于机器人定位是一个非线性、含有较多不确定性因素的问题，因此当前主要采用基于贝叶斯滤波的概率推导方法，如卡尔曼滤波器、多峰值估计法、马尔科夫定位和蒙特卡洛法等［3－4］。在实例方面，卡内基梅隆大学与德国伯恩大学基于蒙特卡洛方法，合作研发出博物馆导游机器人Rhino及Minerva，可以从博物馆中任意一个位置出发，较快地实现自定位［5］。

国内对于自定位问题的研究起步相对较晚，主要集中在近10年内。如利用马尔科夫算法对机器人进行定位；利用改进的自适应粒子滤波算法，降低运算复杂度，提升算法稳健性；利用特征粒子提取思想，降低粒子数目；采用改进的Hough密度谱和Fouder－Mellin变换方法来估计机器人的运动参数等［6－9］。

笔者将基于粒子滤波器原理，对已知地图的轮式移动机器人的自定位展开研究。在经典粒子滤波算法的基础上，提出了两个改进策略，可在保证跟踪精度的同时，显著减少计算量:

（1）粒子初始化时，每个粒子的角度经过一次匹配得到，可减少计算量。具体来说，首先估计每个粒子在所有可能方向上与周围环境的距离，然后将这些距离估计值与移动机器人的测距传感器测量值进行匹配，找出最接近该测量值的角度，作为该粒子的初始角度。这样不仅能减少自定位所需要的粒子数，而且能减少在计算移动机器人角度方面的计算量。

（2）采用查表式方法估计距离，可提高定位效率。首先对环境地图进行离散化，其后针对地图中每个小格，进行360度等间隔离散，并计算各角度上该小格与周围环境的距离，将其存为表格形式。当机器人在环境中行走，并获得量测距离时，可以直接调用上述表格文件，通过查表方法，判断各个粒子在各方向上的概率，从而减少自定位的在线计算时间，增强机器人运行及定位的实时性。

1 机器人运动模型

在对轮式机器人分析的过程中，常把机器人建模为轮子上的一个刚体，在水平面上运动。参见图2，建立平面坐标系XOY，则机器人的位置和姿态可以用如下状态向量表示:

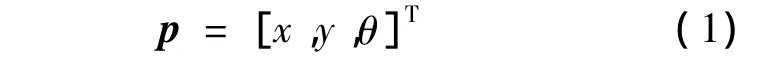
式中:x，y为机器人在二维直角坐标系中的位置坐标；θ为机器人的朝向，即机器人运动正方向与X轴的夹角。

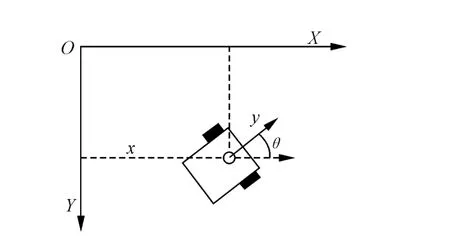
图2 机器人状态示意图

假设在 t1时刻机器人处于状态 S1（x1，y1，θ1），若机器人左右轮都进行匀速运动，经过短暂时间 Δt之后，机器人处于状态 S2（x2，y2，θ2），那么这段时间内机器人的运动可近似看作圆周运动，其运动模型如图3所示。

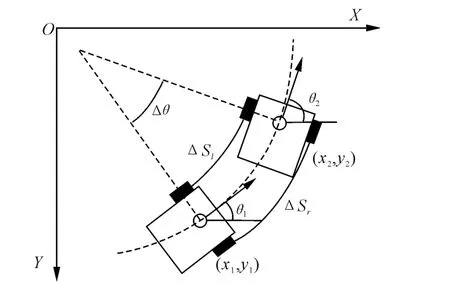
图3 运动模型

则当前状态 S2（x2，y2，θ2）与上一状态 S1（x1，y1，θ1）之间的关系为:

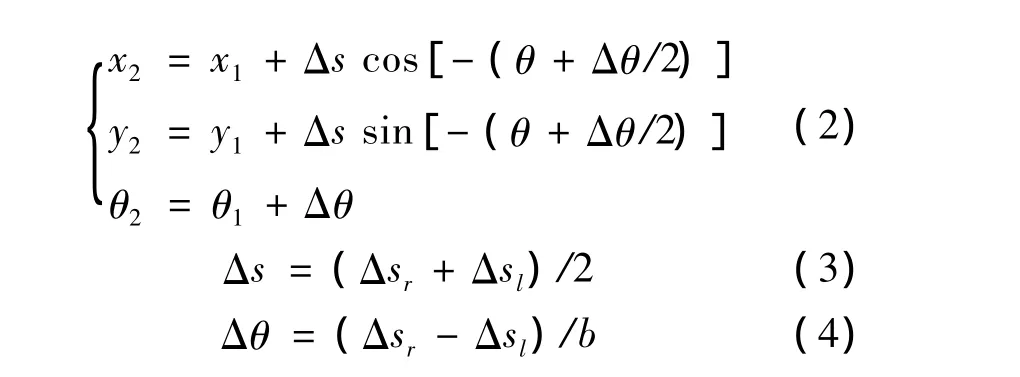
式中:Δsr和Δsl分别为右轮和左轮一次行走的距离；b为机器人同轴两个轮子间的距离；Δs和Δθ分别为机器人一次运动行走的距离和方向的变化，这两个量即为机器人在自身局部坐标系中的移动和转动，式（2）即为局部坐标系与全局坐标系之间的转换公式。

2 移动机器人自定位设计

2.1 移动机器人定位贝叶斯建模

移动机器人定位原理图如图4所示。可以采用概率图来描述移动机器人的运动过程，其中ut为作用于机器人的控制信息，pt为t时刻移动机器人的状态，ct为机器人在t时刻得到的传感器距离信息。

图4 移动机器人定位原理图

可以将机器人定位理解为贝叶斯滤波问题。机器人依据获得的量测信息，以一定的置信度（Belief）确定它的位置:

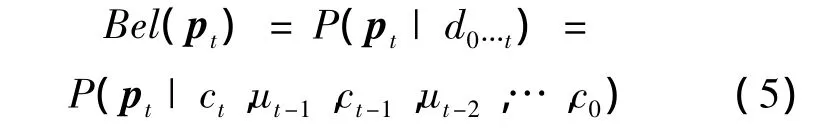
式（5）表示在已知0～t时刻的所有控制数据及观测数据 d0…t={ct，ut－1，ct－1，ut－2，…，c0}的情况下，机器人在t时刻位于状态pt的概率。

结合贝叶斯公式变换可得到:

由于系统具有马尔科夫性，且 P（ct|ut－1，ct－1，ut－2，…，c0）为一常数，因此式（6）可进一步简化为:

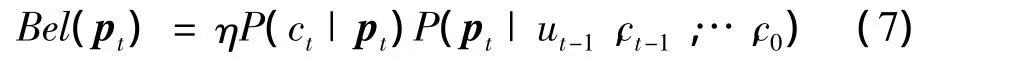
通过对状态空间离散化，则式（7）可以写为:

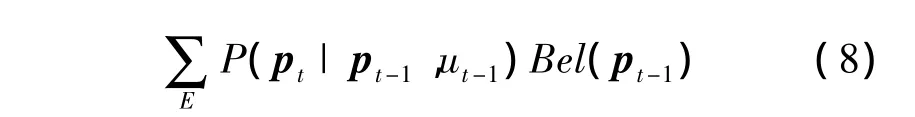
式中，E为离散后的状态空间。

2.2 基于粒子滤波器的数值化实现

式（8）给出了离散状态空间中的定位模型，由于各种先验概率、似然度函数往往不具备解析形式，可能为非线性、非高斯的概率，直接由式（8）来解析求解状态是不可能的。

因此笔者采用经典的粒子滤波器来数值化求解式（8）。粒子滤波器也称为序贯蒙特卡洛方法（sequential Monte Carlo，SMC），是一种在时间序列上的离散、非参数式的贝叶斯滤波方法，能够处理各种非线性、非高斯、多模态问题。

2.2.1 状态方程及量测方程

机器人的定位问题可以描述为:给定一组观测向量Ct，估计机器人当前所在状态pt。其中:Ct={c0，c1，…，ct}为观测序列；pt=［xt，yt，θt］T为机器人在t时刻的位置和朝向。

设移动机器人状态方程为:

式中:ut为机器人的运动控制输入变量；wt为过程噪声。函数f（x）由机器人的运动模型给定，即在式（2）的基础上加上噪声wt，则可得:

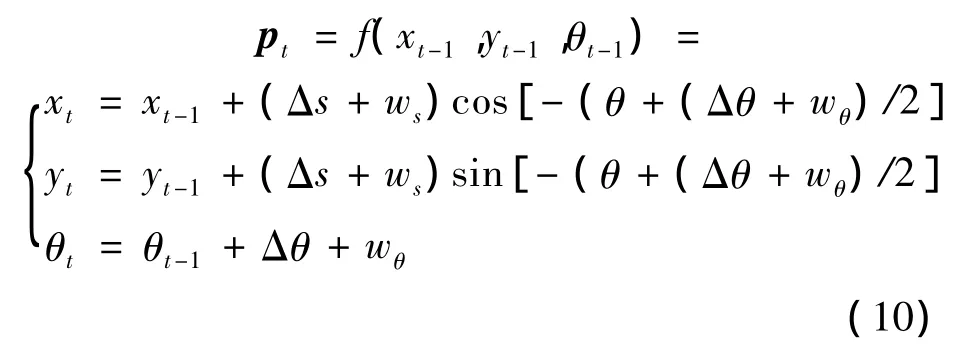
式中，ws和wθ分别为机器人的运动距离和偏转角度的噪声。

系统状态量测方程为:

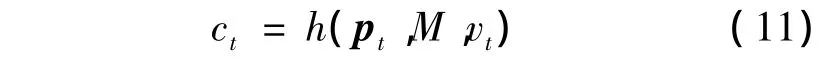
式中:M为环境地图；vt为量测噪声；pt的估计由求解Bel（pt）得到。

2.2.2 初始化粒子

移动机器人自定位程序首先是粒子的初始化。初始的粒子服从均匀分布，即每个粒子出现在图像中任意一个点的概率都是1/N，其中N为移动机器人在地图上可能出现的位置总数。

由式（1）可知，粒子的初始化除了要初始化粒子的位置之外，还要初始化粒子的朝向角度，即θ。因此需要大量的粒子来表示移动机器人所有可能的位置和角度，计算量非常大。

假定θ值按均匀分布生成粒子，即θ～U（0，2π），那么当某个粒子的坐标与机器人的真实2D位置吻合时，该粒子随机生成的θ与机器人真实的方向吻合的概率并不大，从而造成计算浪费。

实际上，在已获得距离量测的情况下，状态向量中角度分量θ是不独立的，其与其他两个分量，即机器人在二维空间的坐标x、y是相关的。因此可以把状态变量分为两个部分，则有式（12）:

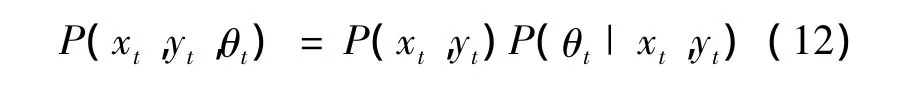
根据式（12），首先基于均匀分布p（xt，yt）～U（M）对二维坐标x，y进行采样（M为环境地图），然后对于每一个粒子，求出该粒子在自己位置上匹配权重最大的角度，将该值作为θ的初始值，这与文献［10］提出的方法有些类似，都是把状态向量分为几个部分，将联合概率分解为条件概率的乘积形式。而笔者的创新之处在于，结合坐标分量和量测来直接估计每个粒子的角度分量。其优点在于既能有效提高粒子的采样质量，又能极大地减少用于确定机器人朝向的粒子数量，并且在以后的定位计算中也不需要再考虑移动机器人的θ值问题，只需根据式（10）将机器人运动产生的θ值的变化量Δθ加到每个粒子的θ值即可，不用再计算移动机器人的θ值。

2.2.3 粒子重采样

在完成粒子的初始化之后，每个粒子的权重也在初始化θ值时赋给了每个粒子。此时就可以找出权重最大的粒子作为本次机器人位置的最佳估计。下一步的工作就是对粒子进行重采样，为下一次估计机器人位置做准备。

重采样的目的是去掉权重小的粒子，同时将权重大的粒子分解成若干个权重较小的新粒子。重采样的思想可以用图5来表示。

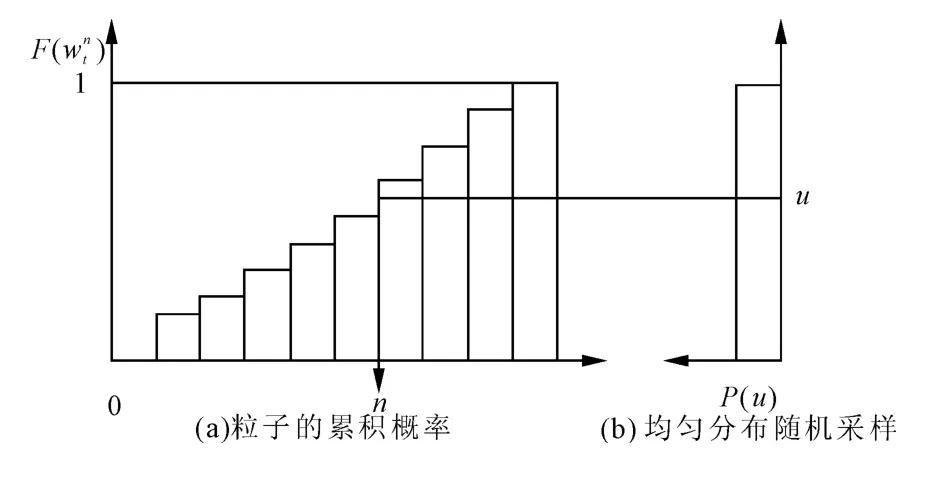
图5 重采样示意图

图5（a）为粒子权重的累计概率分布函数，横坐标为粒子的序号；图5（b）为0～1间均匀分布的随机变量，u为该随机变量的一次采样值重采样过程中，首先计算出粒子概率的累积概率，然后在0～1间按均匀分布随机采样，投影到图5（a）中，投影的位置向下指示出累积概率相应定义域的位置，这就是新粒子的索引。这样共产生L个粒子，其权重都重置为1/L。显然，权重大的粒子就可能会被多次重复采样。

2.2.4 粒子状态预测

完成了粒子的重采样之后，机器人运动一次。根据里程计的返回值由式（3）和式（4）计算出这一次运动后，机器人相对运动前的位置和角度的变化，并由该变化量按照式（10）系统状态方程，更新每个粒子的位置和角度，使每个粒子都能相对于自己上一时刻的位置和角度，作与移动机器人相同的运动。

如机器人向前走了10 cm，每个粒子也按自己的方向向前走10 cm。实际环境中由于受车轮打滑、里程计测量有误差等因素的影响，虽然里程计返回值是10 cm，但机器人很有可能不是走了刚好10 cm。因此式（10）引入了过程噪声wt。

2.2.5 粒子权值更新

在所有粒子都随移动机器人运动后，下一步的工作就是为所有粒子重新计算权值。

基于环境栅格地图，对于每一个粒子，根据该粒子的状态（包含位置及方向），计算出该粒子在该方向上与环境的距离d，并将距离值与移动机器人测距传感器的真实返回值d^相比较，从而求出式（8）中的P（ct|pt）:

式中:C为归一化系数；∑为由传感器量测噪声vt的方差。

由于粒子的数目非常多，如果用实时计算的方式来求解每个粒子的测量值会需要很长的时间。因此，设计了一种基于查表方式的权值更新方法。首先在离线形式下，把机器人在地图中所有可能的位置和姿态列出来，并计算出相应各传感器的距离信息，生成一个二进制文件。

通过查表方法，可以实时地将需要的数据d^从文件中找出来，由式（13）计算量测概率，从而减少了机器人自定位的计算量，缩短了机器人两次运动之间的时间，增加了自定位程序的实时性，但也一定程度地增加了机器人内存的消耗。

基于粒子滤波理论的移动机器人自定位程序的流程图如图6所示。

3 仿真实验及结果分析

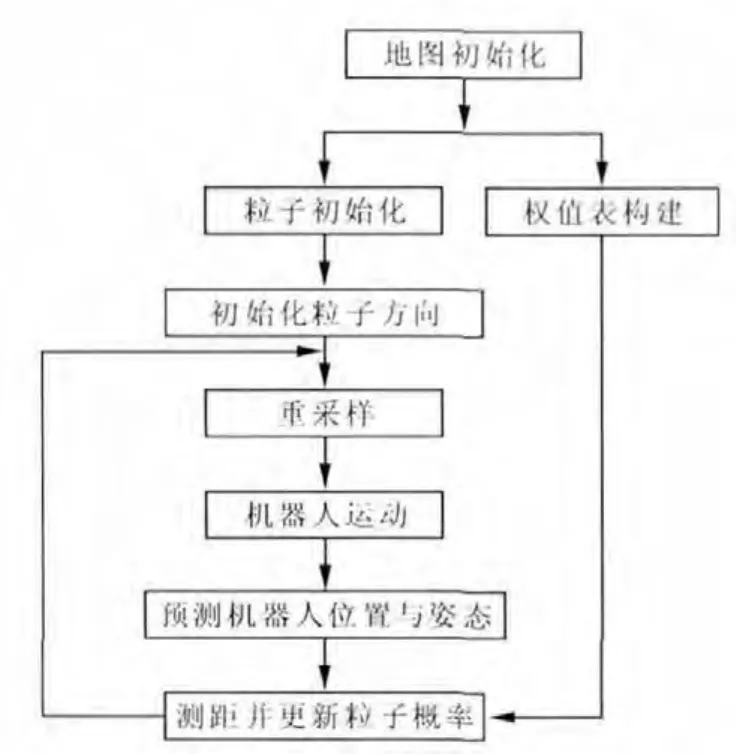
图6 自定位流程图

笔者使用VC2005对算法进行仿真。图7中使用的粒子数为3500，灰色区域为障碍物和墙壁，灰色的点为粒子。实线为仿真程序生成的机器人实际位置，机器人前方两条线的长度表示两个测距传感器的实际测量值；虚线为机器人最优估计粒子的位置和方向，两条射线的长度表示在该位置和方向上，两个测距传感器对应的测量估计值，可以通过查表获得。

仿真使用的地图是由4个房间和1条走廊以及每个房间内的障碍物组成简单结构的环境。由于仿真环境地图比较简单，环境中存在对称的点，则机器人在自定位时，粒子会集中到这些与机器人所在真实环境对称的点附近，只有当机器人运动到独特的位置时，所有的粒子才会聚集到机器人的真实位置附近。

图7（b）为机器人仿真定位程序的第1次定位结果。与图7（a）的初始状态相比，粒子已经开始聚集，不过由于信息还比较少，因此最优的粒子与实际的机器人位于不同房间。

图7（c）为仿真程序的第2次定位结果，与第1次定位的结果相比，粒子又进一步集中，且最优估计状态也正确估计出机器人所在房间。

随着机器人的运动，距离量测信息越来越多，第4次定位后，效果比较明显，参见图7（e），到第6次定位完成后，估计就非常准确了，参见图7（f）。

将笔者提出的算法与经典蒙特卡洛算法进行比较可知，笔者采用了角度计算策略，而经典算法直接对式（1）状态进行采样；笔者采用了查表计算权值，而经典算法是采用在线计算粒子权重的方法。

采用的仿真实验粒子数为3500，运行环境为Windows Xp下 VS2005，奔腾双核 2.6 G，1 G 内存。比较结果如表1所示，可以发现笔者算法在耗时及收敛速度上具有优越性。

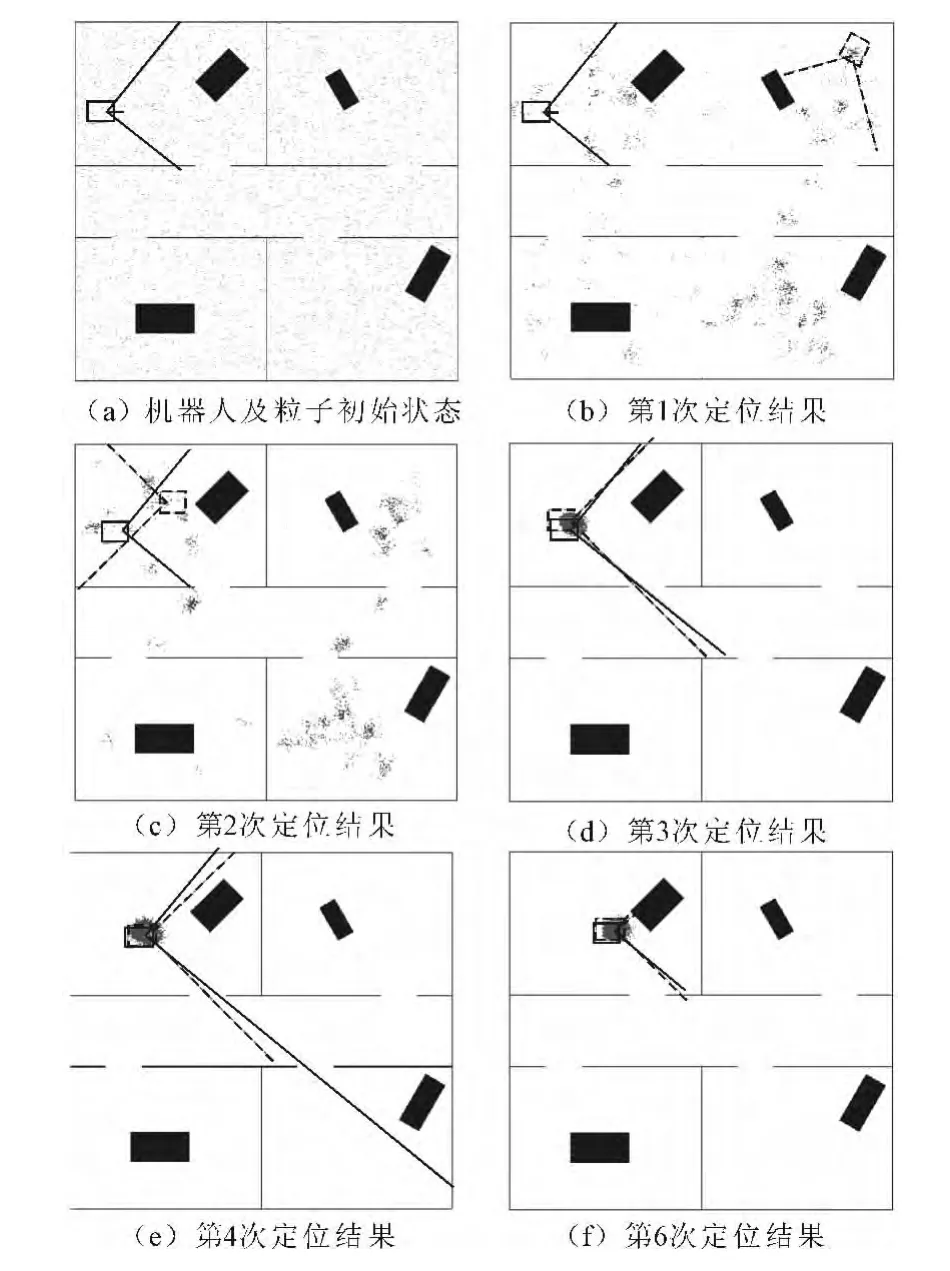
图7 笔者算法定位仿真

表1 笔者算法与经典蒙特卡洛算法比较

4 结论

笔者针对经典蒙特卡洛定位算法，提出了两种改进策略。首先粒子初始化时，每个粒子的角度经过一次匹配得到，从而减小了计算量。其次，采用离线方式计算场景的权重表，在定位过程中，经过直接查表，可极大地减少定位的时间消耗。

通过与经典蒙特卡洛定位算法的比较，笔者的算法具有计算量小，收敛速度快的优点。

［1］蔡自兴.机器人学［M］.北京:清华大学出版社，2000:16－25.

［2］IEGWART R，NOURBAKHSH I R.自主移动机器人导论［M］.李仁厚，译.西安:西安交通大学出版社，2006:21－120.

［3］DURRANT－WHYTE H，BAILEY T.Simultaneous localization and mapping:part I［J］.Robotics ＆ Automation Magazine，IEEE，2006，13（2）:99 －110.

［4］BAILEY T，DURRANT －WHYTE H.Simultaneous localization and mapping（SLAM）:part II［J］.Robotics＆ Automation Magazine，IEEE，2006，13（3）:108－117.

［5］THURN S，BEETZ M，BENNEWITZ M，et al.Probabilistic algorithms and the interactive museum tourguide robot minerva［J］.International Journal of Robotics Research，2000，19（11）:972 －999.

［6］方正，佟国峰，徐心和.基于贝叶斯滤波理论的自助机器人自定位方法研究［J］.控制与决策，2006，21（8）:841－862.

［7］曾慧，吴福朝，胡占义.基于平面激光测量的移动机器人自定位方法［J］.自动化学报，2007，33（2）:138 －144.

［8］刘承俊，原魁，邹伟，等.基于特征粒子的Monte Carlo自定位方法［J］.机器人，2006，28（1）:30 －35.

［9］陈卫东，张飞.移动机器人的同步自定位与地图创建研究进展［J］.控制理论与应用，2005，22（3）:455 －460.

［10］OLIVIER C，SIMON J G，ERIC M.An overview of existing methods and recent advances in sequential Monte Carlo［J］.IEEE，2007，95（5）:654 －662.