基于背景噪声的图像伪作检测
2014-10-21

摘 要:一幅真实的数字图像中的噪声特征具有一致性,而由多幅数字图像拼接的合成图像的噪声特征没有一致性。本文,我们利用小波变换多分辨率的特点,依据原图像和篡改后图像的平均运算、细节运算不同的原理,采用了支持向量机(SVM)分类器的诸多常用核函数中的S形核函数进行分类识别,提出了基于图像背景噪声的图像伪作检测算法。该方法对于识别合成的数字图像具有显著效果,对合成图像的篡改操作有较好地鲁棒性。
关键词:噪声;篡改;小波变换;支持向量机
中图分类号:TP391.41
在当今互联网时代,信息尤其是图像信息的真实性对于商业、军事、媒体等来说都至关重要,但是由于相应的图像篡改技术在不断升级,使得如何识别初始图像和篡改图像成了研究的难点,也是学术界关注的重点之一。目前研究图像篡改的检测方法,分为主动与被动技术两种。主动技术包括给数字水印和数字签名,他们都有在图像中添加附加信息等弊端;被动技术是根据图像本身信息来判断其是否篡改,包括四种常见的检查方法:采用SURF提取图像不变量特征采用最近邻法进行特征匹配的图像复制粘贴篡改检测技术[1];基于质量评价量和方差分析以及基于相位一致性的篡改检测技术[2-3];利用相机模板噪声与待测图像相匹的篡改检测技术[4];利用图像高阶统计量来计算噪声标准差的不一致性的篡改检测技术[5-6]。本文通过小波变换获得图像噪声,再运用支持向量机分类器进行特征分析真实图像和篡改图像,从而识别图像是否被篡改。
1 小波变换及其原理
1910年,Haar最早提出小波规范正交基;1981年,Morlet首次提出“小波分析”的概念,它是对傅里叶变换和短时傅里叶变换的改进,成功用于地质数据处理;1986年,Meyer通过创造了具有衰减性的ψ(x)光滑函数,其二进伸缩和平移: ;j,k∈Z是函数空间L2(R)的一个标准正交基,标志着小波分析取得了突破进展,同年S.Mallat和Y.Meyer提出多分辨率概念和快速小波变换算法[7],此时小波变换的理论框架就已成熟。与傅里叶变换只能反映图像的整体特征但缺乏时空域上局部化的功能相比,小波变换可通过伸缩平移运算对信号逐步进行多尺度细化,可以进行高频处时间细分、低频处频率细分,通过自动适应时频信号分析要求,聚集到信号的任意细节。
本文研究的基于背景噪声的图像伪作检测算法主要也是基于小波变换,而信号压缩则是小波变换的核心思想。具体来说,设多元素的信号为{X1,X2,X3,X4},平均运算和细节运算表示为:{a1,0,a1,1,d1,0,d1,1},篡改越多,则丢弃的细节信号越多,原信号的小波变换是:{a0,0,d0,0,d1,0,d1,1},其中基于不同层次的平均信息、细节信息的分辨率信息依次是:{X1,X2,X3,X4}表示最高分辨率信息;{a1,0,a1,1}表示次高分辨率平均信息;{d1,0,d1,1}表示次高分辨率细节信息;{a0,0}表示最低分辨率平均信息;{d0,0}表示最高分辨率细节信息。对于长度为2n的信号Sn={Sn,t|0≤1≤2n},平均和细节记作:
多级Haar小波变换分解和重构过程可用图1表示:
2 分类器解釋
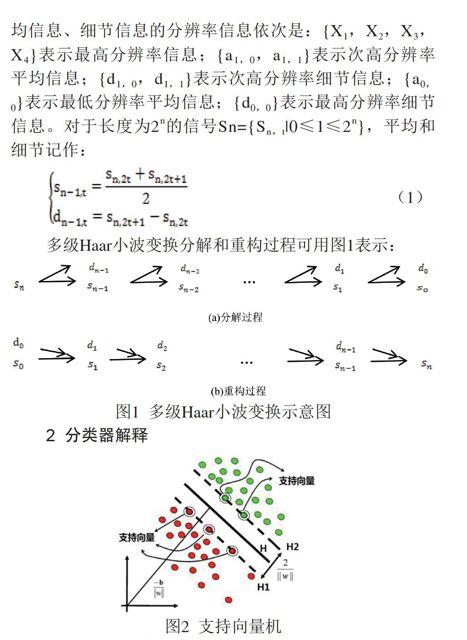
利用小波变换原理获得图像噪声特征,然后采用支持向量机对真实原图像和篡改部分图像进行分类和识别,在本文采用的是支持向量机(SVM)[8]分类器中的诸多常用核函数S形核函数K(xi,xj)=tanch(v(xi*xj)+t)对噪声特征进行分类。前人研究中有多项式内积函数、径向基核函数的支持向量机,但未有文献研究Sigmoid核函数。SVM它的主要思想是将非线性可分样本的输入向量映射到高维度Z空间,从而找到超平面,在图像识别和函数运算方面具有诸多优势。在两个平面间我们找那么一个超平面,它使得分类间隔最大,这种分类器称之为支持向量机,如图2。通过支持向量机,可以有效地将图像原始部分和发生篡改的部分进行有效的分离。
3 实验结果与分析
为了验证本文算法是否有效,选取了三幅256*384的彩色图像进行了灰度处理,再原始图像分别进行增加、减少、转移等篡改操作,篡改后的图像如下,并对其进行检测。
在实验中,我们针对上面的三幅图像共进行了两次检测。在第一次检测时,我们发现只有一部分被篡改的图像部分能够被检测出,但仍然存在漏检甚至误检的情况,所以我们利用改进后的算法进行重新的检测与定位。在第二次检测与定位之前,我们先对篡改后的图像进行了相关性强弱的判断,这一次的结果精确度较第一次有所提高,尤其是误检和漏检情况得到了明显改善,效果也比较理想。
通过Matlab我们对每个图像进行了8*8和8*12的分块检测,分块后,确定了每块的平均值;然后对每个子块进行归类(类别包括均匀字块、边缘字块还是纹理字块),而归类就是通过SVM来完成的。再开始对每个字块进行编码,而解码过程是编码过程的逆过程。研究结果发现8*8的漏检和错检率较高,而8*12分块结果较好,这表明分块的大小可能对于识别篡改部分也有所影响。另外,阀值的选取也对噪声处理产生直接影响。因为我们利用小波变换处理篡改后图像的主要步骤是:首先是利用小波阈值来对图像进行去噪处理,优先处理小波分解后大于或小于阀值部分;去第二步是再利用小波系数重构去噪后的图像。对于给定的小波系数,噪声越大,阀值越大。所有对于噪声的预估决定了阈值的设定,如果太小,难以实现有效去噪;如果太大,将可能将原始图像局部区域也被覆盖了。本文采取的是目前研究最为常见的VisuShrink全局同一阈值: ,其中σ是噪声信号的标准差(度量噪声强弱),N为信号长度。
具体来说,在图像-房子中噪声点与周围像素点灰度差别较大,表现为高频信号。当噪声强度增大,图像原本的灰度将成为次高信号,被高频影响而难以识别。在进行第一级小波分解时,如果篡改后的图像噪声越多,小波分解的高频系数的标准差之比将趋于一个固定值。与之相反,对于图像树的篡改操作,由于是删除了一朵花,所以表现的是图像模糊,这就意味着用相对低频的信号代替了边缘突变的高频信号。在进行第一级小波分解时,如果篡改后的图像越模糊,那么小波近似系数和原始图像的标准差之比会越大。
总之,对图像小波分解的高低频数关系做阈值处理能够判断图像的真假,有助于我们识别图像是否被篡改。
4 总结与展望
由于不同图像的背景噪声强度不同,所以在提出图像篡改识别算法时关键步骤是对噪声进行估计,本文采取的方法是对图像进行了两次全图二维小波分解,这样既能够保证算法的精确度也一定程度降低了计算的负责度,其他相关研究可以借鉴该方法。
我们在本文中分别针对图像常见的三种篡改方式:增加、修改、减少操作都进行了实验分析和检测。我们基于图像背景噪声提出了一种新的图像篡改的检测算法,主要利用了小波分析多频率特点,有效地识别篡改手段和篡改图像部分,该算法为图像鉴定和法医取证方面提供了一种新的应用可能性,具有一定参考价值,但对于复制粘贴、重采样等操作的篡改检测效果不理想,以后在这一方面进行下一步研究。
参考文献:
[1]张静.基于像素匹配的图像“复制-粘贴”篡改检测算法[J].天津大学学报,2009(08):713-720.
[2]黄启宏.一种改进的相位一致性图像特征检测方法[J].电讯技术,2006(06):172-176.
[3]吴昌柱,王庆.基于相位一致性的兴趣点检测方法[J].西北工业大学学报,2006(02):199-204.
[4]杨弘,周治平.基于模式噪声的手机图像篡改检测[J].计算机系统应用,2013(09):210-213.
[5]卢燕飞.基于图像背景噪声特性的篡改检测[J].信号处理,2012(09):1299-1306.
[6]王虹.基于量化噪声的JPEG图像篡改检测[J].计算机工程与应用,2012(19):205-208.
[7]董卫军.基于多小波变换的图像去噪[J].计算机应用与软件,2007(12):32-34.
[8]丁世飞.支持向量机理论与算法研究综述[J].电子科技大学学报.2011(01):2-10.
作者简介:洪拥筠(1987-),男,安徽安庆人,硕士研究生,主要研究方向:智能信息处理、图像处理。
作者单位:贵州大学 大数据与信息工程学院,贵阳 550025
