基于多智能体的循环流化床锅炉燃烧控制系统
2014-10-21吉晓青孙荣霞
吉晓青 孙荣霞


摘 要:由于循环流化床锅炉燃烧系统具有参数分布广、非线性、时变和大滞后等控制难题,因此分析了该系统的结构与工艺特点。运用多智能体建模方法,将系统进行机理分析分解为若干个子系统,并找出子系统输入输出变量之间的关系,建立被控对象的子系统的数学模型。采用多智能体预估和控制方法,给出循环流化床锅炉燃烧系统的多智能体预估控制算法。仿真结果表明采用该建模和控制方法,能够取得满意的控制效果。
关键词:循环流化床锅炉;多智能体;预估;控制
中图分类号:TP13;TP273
近年来,我国北方雾霾越来越严重,究其原因,我国的能源结果以煤炭为主,火电装机总量高达8.81亿千瓦,因此我国大力发展清洁燃烧技术。循环流化床锅炉以其燃烧效率高、污染少、燃料范围广的优势,在近年来得到大规模的应用。在控制过程中,床层溫度是一个直接影响锅炉能否经济安全运行的重要指标。但是由于循环流化床锅炉燃烧过程中伴随着强烈的热交换和化学反应,而且煤炭燃烧具有大的热惯性,通过给煤量调节床层温度滞后较大,这些情况大大增加了循环流化床锅炉建模的复杂性,因此采用普通的控制手段,很难有良好的效果。
循环流化床锅炉燃烧过程存在着复杂的流体动力学特性和传热传质特性,难以得到被控对象的精确模型,目前大部分的控制系统数学模型是依靠原始数据辨识或者依赖技术人员经验积累来实现的。文献[1]在总结研究循环流化床锅炉的动态特性后,建立了循环流化床锅炉的自整定智能控制器并成功应用于国产75t/h循环流化床锅炉床层温度的控制。文献[2]针对循环流化床锅炉汽温被控对象的高阶特性,将Smith预估器应用到大滞后系统中,设计出一种结合系统数学模型,参考内膜原理的自适应解耦控制系统。然而,循环流化床锅炉燃烧系统存在着大惯性、强耦合以及调节给煤量的大滞后特性,致使被控对象难以控制;Smith预估器对于大滞后系统来说要求得到系统被控对象的精确数学模型,否则一旦模型误差发生大的变化,系统可能进入不稳定状态。
近年来,多Agent系统MAS(Multi-agent System)已成为一个热门的研究方向。Agent模型最初是作为一种分布式智能计算模型被提出来的。二十世纪八十年代Bratman[4]提出了Agent的基本模型,模型包含三个基本的要素:信念(Belief)、期望(Desire)和意图(Intention),各自表示其Agent所具有的认知、能力以及要实现的意图,各个Agent的独立行为动作,都是基于三个基本要素,通过与外界以及和其他Agent之间的交互来完成的。
对于现实中复杂的、大规模的系统有必要采用多Agent系统,多Agent不但具有求解自身内部的参数,而且还可以通过相互合作,来解决系统整体复杂的问题。它们具有如下特点:
(1)各个Agent具备处理自身信息和解决自身问题的能力;
(2)各个Agent独自存储并且处理自身的数据;
(3)各个Agent之间是异步通信和并行计算的。
MSA系统由多个Agent组成,它们通过相互之间以及与环境之间通讯、协作来共同完成复杂的任务,和传统建模方法和控制方式比起来,具有更灵活的适用性、更高的效率、分布式的感知与作用、内在的并行性[5]、改良的系统性能、容错控制、鲁棒性。因此多Agent系统近年来得到学者们深入的研究,并且在医学、航天和交通控制等领域也得到广泛的应用。
本文在分析循环流化床锅炉燃烧过程系统内部结构和工艺特点的基础上,采用一种多智能体模型描述不确定、大滞后、强耦合的循环流化床锅炉燃烧过程的运动特性,将复杂的系统分解为多个子系统模型。子系统数学模型比整体系统模型更易求得而且可以大大降低输出对输入的时延,采用一种多智能体预估控制算法,以期提高控制效果的满意程度[6]。
1 循环流化床锅炉燃烧系统结构分析与多智能体建模
循环流化床锅炉燃烧系统结构复杂,本文采用多智能体建模方法,通过利用Agent的局部连接规则、机理方程和局部细节模型,建立该复杂系统的一种多智能体模型。
循环流化床锅炉按结构分,由炉体、给煤系统、一次风系统、二次风系统、分离器、回料器、尾部烟道等组成。通常锅炉本体分为密相区和稀相区两部分。
循环流化床锅炉燃烧过程可以看成是由相互关联的四个部分组成,即密相区、稀相区、分离器和回料器,假设每一部分中包含有一个Agent模块,这些Agent模块分别为Agent1、Agent2、Agent3、Agent4。它们能够长期获取数据,发现规则并且建立周期性的模型。分别对这四个部分进行分析,列出动态物料平衡和动态能量平衡方程,用大量实例数据训练Agent模块,建立子系统智能体模型。
根据某型循环流化床锅炉的运行状况,提出了如下简化假设:
(1)不考虑石灰石的加入及其化学反应;
(2)各部分均为均质对象,即温度和密度均匀分布;
(3)锅炉与外界完全绝热,密封良好;
(4)分离器内没有换热装置,且不发生燃烧反应。
1.1 建立密相区Agent模型
密相区是锅炉本体的下半部分,燃烧的颗粒浓度较高。密相区具有复杂的多输入多输出结构,建立以煤、一次风、回料器、稀相区对密相区的沉降为输入,以排渣、密相区对稀相区的扬析为输出的动态平衡方程。
密相区床料质量平衡方程为:
式中,MA1为密相区质量,Fc为给煤量,FA1,A2为稀相区对密相区的扬析量,Fd为排渣量, 为单位时间内密相区内煤炭燃烧量,FA4,A1为回料器返料量,FA2,A1为稀相区对密相区的扬析量。相对于给煤量Fc和燃烧量 ,其他各分量对密相区质量的影响较小,可以忽略不计。
密相区燃烧热量平衡方程为:
QF1为单位时间一次风带入的热量,可表示为:
QF1=Vg1Sg1CgTA1 (5)
其中,Vg1为一次侧风速,Sg1为一次侧风入口截面积,Cg为空气比热容。
Qc为单位时间给煤带入的热量;
Qc=FcCgTA1 (6)
QA4,A1为单位时间返料带入的热量。
QA2,A1为单位时间稀相区对密相区沉降物料的热量;QA1,A2为单位时间密相区对稀相区扬析的热量。
QA2,A1=FA2,A1CgTA1=α1MA1CcTA1 (7)
QA1,A2=FA1,A2CgTA1=(1-α1)MA1CcTA1 (8)
其中,α1为沉降分离效率修正因子,一般取0.05。
Qd为单位时间排渣排出的热量;
Qd=FdCcTA1 (9)
為单位时间密相区煤燃烧产生的热量;
(10)
其中,Hc为煤炭的热值,Carvalho[11]给出了燃烧速率 的关联式。
(11)
式中,k1为燃烧速率系数;dc1为密相区煤炭颗粒直径;ρo2为密相区氧气浓度,ρc1为密相区煤炭颗粒浓度。
为单位时间密相区辐射输出的热能。
(12)
其中,β1为传热系数;S1为受热面;Tw为受热面温度。
将式(3)-(12)带入到热量平衡方程式(2)中,可得:
假设计算机采样周期为ΔH(ΔH足够小)时,式(12)可近似为:
其中,d0为密相区输出对一次风的滞后时间。从上式可以看出,在实际控制过程中,一般通过调节一次风速Vg1及密相区颗粒浓度ρc1来调节温度的。
整理得:
(15)
式中,Z12(k)为密相区的系统输出温度TA1,Z11(k-d0)为一次侧输入风速Vg1,Z10(k)为煤炭颗粒浓度ρc1,v1是扰动。
(16)
其中,a、b是与密相区质量MA1有关的参数,c、d与煤炭颗粒的直径和氧气浓度有关。可以用最小二乘法来辨识式(15)中的参数。
令:
Y=[Z12(k+1)Z12(k+2)…Z12(k+n)]T
(17)
其中,Y=AUT,即可通过A=Y(UT)′辨识出系统参数,由于密相区质量MA1会缓慢变化,所以式(16)中的模型参数会变化,所以在线用最小二乘法辨识这些参数,最终得到密相区的Agent模型。
1.2 稀相区Agent模型
同样地把稀相区Agent看成系统整体中的其中一个Agent2,稀相区有三个输入和二个输出,建立其动态能量平衡方程。
稀相区床料质量平衡:
(18)
式中,MA2为稀相区质量;FA3,A2为分离器对稀相区的沉降速率;FA2,A3为稀相区对分离器的扬析速率; 为单位时间内稀相区内煤炭燃烧量。
稀相区动态能量平衡方程为:
(19)
式中, (20)
其中,QA2为稀相区能量,TA2为稀相区温度。
QF2为单位时间二次风带入的热量;
QF2=Vg2Sg2CgTA2 (21)
其中,Vg2为二次侧风速,Sg2为二次侧风入口截面积。
QA3,A2为单位时间分离器对稀相区沉降物料的热量,QA2,A3为单位时间稀相区对分离器扬析物料的热量;
QA3,A2=FA3,A2CcTA2=α2MA2CcTA2 (22)
QA2,A3=FA2,A3CcTA1=(1-α2)MA2CcTA2 (23)
其中,α2为沉降分离效率修正因子。
为单位时间稀相区煤炭燃烧产生的热量;
(24)
其中,单位时间内稀相区内煤炭燃烧量 可由式(24)确定。
(25)
式中,k2为燃烧速率系数;dc2为稀相区煤炭颗粒直径;ρc2为稀相区煤炭颗粒浓度。
为单位时间稀相区辐射输出的热能。
(26)
其中,β2为传热系数;S2为受热面。
由上述公式联立可得:
(27)
同理,可得稀相区运动方程:
(28)
式中,Z23(k+1)为稀相区系统的输出温度TA2,Z20(k-d1)为二次侧输入风速Vg2,Z12(k)为稀相区的煤炭颗粒浓度ρc2,v2为扰动,d1为滞后时间。
(29)
同样地,用最小二乘法可辨识得到稀相区Agent模型。
相应地建立分离器(Agent3)和回料器(Agent4)的动态能量平衡方程。
(30)
式中,QM为废气带走的热量。
QM=(Vg1Sg1+Vg2Sg2)CgTA3 (31)
同理,将式(27)整理得:
(32)
这样通过辨识可得到分离器Agent数学模型。回料器一般采用高温发料,运行稳定时,可认为回料器中能量基本保持不变。
即: (33)
2 多智能体预估控制算法实现
由于循环流化床锅炉结构复杂,传统控制思想存在着控制效率低下,抗干扰能力不足,难以克服系统中的大滞后和强耦合等问题。多智能体预估控制是将模型信息与检测信号分散化,采用模型误差反馈校正,滚动优化控制参数,能够控制复杂的被控对象[7-9]。
表示子单元ΣA1的智能体预估器, 表示子单元ΣA2的智能体预估器。各个子单元智能体预估器之间的通信依靠系统的物理结构进行,我们假设在子单元上设计的预估算法可以得到整体系统运行状况。
假设子单元ΣA1的控制输入相对于控制输出的滞后是D12,子单元ΣA2的控制输入相对于控制输出的滞后是D23。因此可以得出预算法:
式中: 、 分别是Z12、Z23的预估值。
假设Zij的期望值是 ,并且系统输入输出的期望与预估值之间存在某种关系,即:
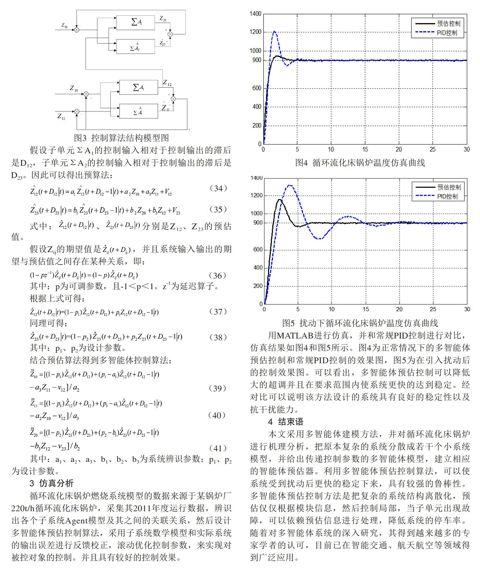
其中:p为可调参数,且-1 根据上式可得: 同理可得: 其中:p1、p2为设计参数。 结合预估算法得到多智能体控制算法: 其中:a1、a2、a3、b1、b2、b3为系统辨识参数;p1、p2为设计参数。 3 仿真分析 循环流化床锅炉燃烧系统模型的数据来源于某锅炉厂220t/h循环流化床锅炉,采集其2011年度运行数据,辨识出各个子系统Agent模型及其之间的关联关系,然后设计多智能体预估控制算法,采用子系统数学模型和实际系统的输出误差进行反馈校正,滚动优化控制参数,来实现对被控对象的控制。并且具有较好的控制效果。 用MATLAB进行仿真,并和常规PID控制进行对比,仿真结果如图4和图5所示。图4为正常情况下的多智能体预估控制和常规PID控制的效果图,图5为在引入扰动后的控制效果图。可以看出,多智能体预估控制可以降低大的超调并且在要求范围内使系统更快的达到稳定。经对比可以说明该方法设计的系统具有良好的稳定性以及抗干扰能力。 4 结束语 本文采用多智能体建模方法,并对循环流化床锅炉进行机理分析,把原本复杂的系统分散成若干个小系统模型,并给出传递控制参数的多智能体模型,建立相应的智能体预估器。利用多智能体预估控制算法,可以使系统受到扰动后更快的稳定下来,具有较强的鲁棒性。多智能体预估控制方法是把复杂的系统结构离散化,预估仅仅根据模块信息,然后控制局部,当子单元出现故障,可以依赖预估信息进行处理,降低系统的停车率。随着对多智能体系统的深入研究,其得到越来越多的专家学者的认可,目前已在智能交通、航天航空等领域得到广泛应用。 参考文献: [1]牛培峰.自整定智能控制器及其应用[J].自动化学报,1996(02):215-218. [2]Liu X W, Lu W L, Chen T P. Consensus of multi-agent systems with unbounded time-varying delays[J]. IEEE Transactions on Automatic Control, 2010, 55(10):2396-2401. [3]陈铁军,邱祖廉.结构分散模型及其应用[J].自动化学报,1992(06):655-661. [4]Jeff Y C P, Tenenbuam J M. An intelligent agent framework for enterprise integration[J]. IEEE Tarns. Systems, Man and Cybernetics,1991, 21(6):1391-1408. [5]刘军志,朱阿兴.分布式水文模型的并行计算研究进展[J].地理科学进展,2013(04):538-547. [6]Qiang MA, Da-ping XV. ADRC with synthesis tuning algorithm for superheating steam temperature of CFBB[J]. Proceedings of the Seventh International Conference on Machine Learning and Cybernetics, Kunming, 12-15 July 2008. [7]席学军,姜学智.循环流化床锅炉燃烧系统的自抗扰控制[J].清华大学学报,2004(11):1575-1579. [8]于希宁,王慧.模糊控制在循环流化床锅炉床温控制中的应用[J].华北电力大学学报,2005(03):43-46. [9]周树孝,石炎福.基于小波除噪和神经网络理論的气固流化床颗粒浓度预测[J].石油化工,2003(03):224-229. [10]毛新军,胡翠云.面向Agent程序设计的研究[J].软件学报,2012(11):2885-2904. [11]覃威宁,郑天舒.基于Multi-Agent的实体建模与时间同步方法研究[J].系统仿真学报,2014(09):1933-1938. [12]梁晓龙,孙强.大规模无人系统集群只能控制方法综述[J].计算机应用研究,2015(01):41-46. [13]冯茜,王磊.仿人智能协调控制在循环流化床锅炉燃烧控制系统中的应用[J].计算机测量与控制,2014(10):3158-3160. [14]周星龙,谢建文.330MW CFB锅炉炉膛壁面颗粒流率分布测量[J].动力工程学报,2014(10):31-36. 作者简介:吉晓青(1987.09-),女,河北任县人,硕士研究生,研究方向:检测技术。 作者单位:河北大学 电子信息工程学院,河北保定 071002
