纳希瞬时单位线参数优化研究
2014-10-21马海波董晓华
马海波 董晓华 刘 冀
(三峡大学 水利与环境学院,湖北 宜昌 443002)
瞬时单位线由纳希1957年提出,指在流域上分布均匀的一个单位瞬时脉冲入流,在流域出口断面所形成的地面径流过程线,也就是流域降雨径流系统的单位脉冲响应函数[1-6].与经验单位线相比,瞬时单位线理论性强,数学推导严密,在一定程度上反映了流域的汇流特性,且该单位线只有两个参数,并且适用于资料缺乏地区,从而利于进行流域降雨径流关系的理论研究,且模型的地区综合实用性非常强,目前在国内外许多流域都得到了广泛的应用[5,7-8].
目前纳希瞬时单位线的推求方法主要是采用统计数学中的矩法,由于矩法本身受计算时段长度的影响较大,导致利用该方法计算出来的瞬时单位线经过S曲线转换得到的时段单位线,进行还原洪水计算时,计算得到的洪水过程与实测的洪水过程差别较大,这在很大程度上限制了瞬时单位线的进一步应用[8-9].为了解决这一问题,目前有学者提出了应用遗传算法求解瞬时单位线的参数,计算结果表明,利用这种方法得到的瞬时单位线对地面径流过程的还原效果要优于应用矩法推得的瞬时单位线还原效果.但是较之矩法,遗传算法的计算繁琐,且计算时间长,计算效率不高.为了解决目前单位线优化方法精度、效率不高的问题,本研究拟建立一套对瞬时单位线参数优化的方法:即先由矩法分析出参数的大致取值,然后再由梯度搜索法在参数的大致取值范围内对参数进行寻优,最后通过实例分析验证本方法的可靠性.
1 瞬时单位线的参数优化问题
1.1 由瞬时单位线计算S曲线
目前,流域洪水预报中常用的纳西瞬时单位线模型为[1,10-11]

式中,u(t)为瞬时单位线与时间t相对应的纵坐标;t为时间;n,k为模型的两个参数,n的物理意义为瞬时单位线定义设定的线性调解水库的个数;K的物理意义为瞬时单位线定义的线性水库的传播时间;Γ(n)为伽马函数,其定义为Γ(n)=dt;e为自然对数的底.
实际应用中,一般是先把瞬时单位线u(0,t)转化为S(t)曲线,然后由S(t)曲线推求无因次时段单位线u(Δt,t),再由无因次时段单位线u(Δt,t)推求时段单位线q(Δt,t),具体推算公式为

本次研究中,对瞬时单位线积分在Matlab平台上实现,Matlab函数库提供了3种用于数值积分的函数[12],分别为梯形法积分函数(trapz)、Simpson递归法积分函数(quad)以及Lobatto积分法函数(quadl),其中Lobatto积分法较之前两种积分方法精度更高.故本次研究采用Lobatto积分法进行计算,具体算法实现为
1)建立瞬时单位线函数
function y=iuh(u)
n=2.07;
y=1/gamma(n)*u.^(n-1).*exp(-u)
2)对瞬时单位线进行积分
st(j,1)= quadl('iuh',a,b)
式中,j为单位线时段数,a,b为积分上下限.当S(j,1)≥0.999 9时,可停止计算,此时,由于S曲线的最大值为1[6],因此当积分计算停止时,若S曲线的最大值为1,则此积分结果即为S曲线;若S曲线的最大值不为1,则可在S曲线的尾部再加上一个数值1即得到最终的瞬时单位线的S曲线.
1.2 由S曲线推求时段单位线
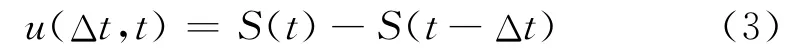
式中,S(t-Δt)是由S(t)向后错Δt时间(净雨时段长).
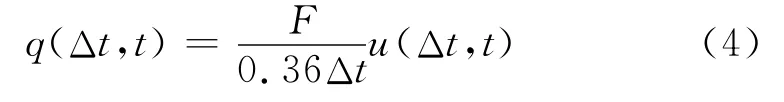
式中,q(Δt,t)为时段长为Δt的时段单位线(m3/s);F为流域面积(km2).
设h(t)为地面净雨过程,则由(4)式求得的时段单位线,可还原地面径流过程Q(t)为
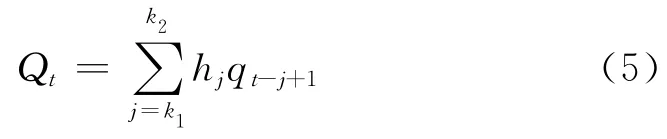
式中,hj为第j个时段的净雨,k1、k2为对流域出口断面流量有影响的净雨时段的累积上下限,其值取决于地面径流时序t与净雨时段数m以及单位线时段数n之间的大小关系,即
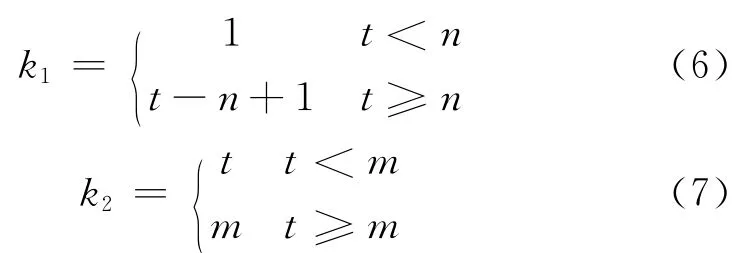
1.3 汇流模型优化问题的提出
由于实际洪水预报中,一般对洪峰点附近的预报精度要求较高,因此,本研究以流域出口断面实测流量与用瞬时单位线还原流量之间的加权残差绝对值最小为原则,建立最优化问题来估计瞬时单位线的两个参数,该最优化问题可以表述为

式中,Qc(t)为用瞬时单位线还原计算得到的流域出口断面流量过程,Qs(t)为实测的流域出口断面流量过程,w(t)为权函数.
该优化问题用常规方法处理很困难,首先借助矩法对参数的取值范围进行确定,然后再由梯度搜索法求解该最优化问题[13-14].
2 应用实例
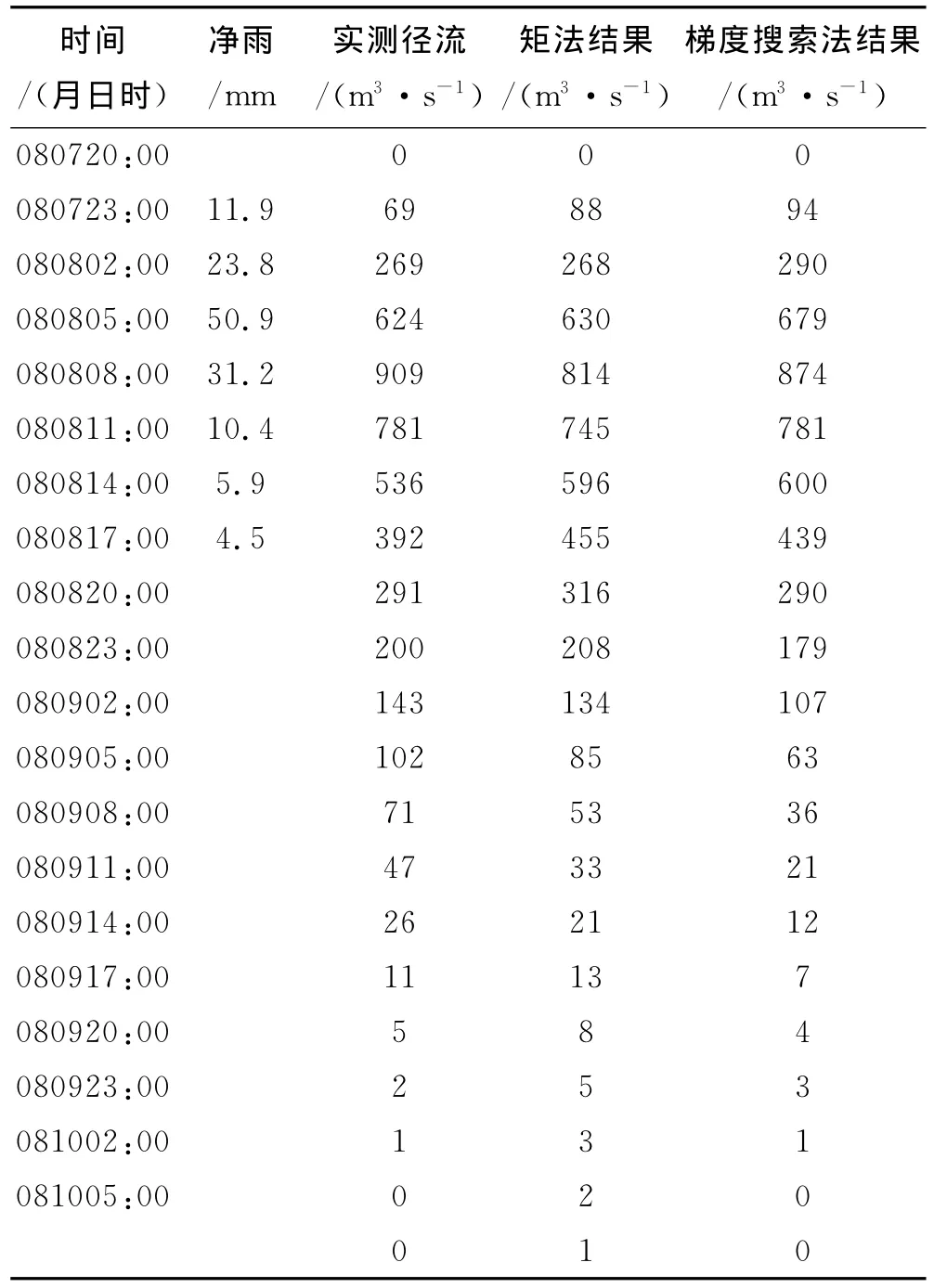
表1 某站的净雨过程、实测和还原径流过程

图1 瞬时单位线还原径流过程图
从表1及图1可以看出,梯度搜索法优化得到的瞬时单位线以及由矩法得到的瞬时单位线还原径流过程与实测径流过程绝对误差加权之和分别为32和43,且在洪峰附近,梯度搜索法较之矩法还原的精度更高,矩法在洪峰处的还原的相对误差为10.45,而梯度搜索法的相对误差仅为3.85%,这对于在实际的洪水预报中准确预报洪峰值具有重要意义.
3 结 论
鉴于应用矩法得到的瞬时单位线还原洪水过程时,还原的洪水过程与同次实测洪水过程拟合效果不佳,尤其是洪峰处的拟合效果较差的现象,本文提出了参数优选的最优化模型,并提出了在应用矩法得出基本参数的基础上,用梯度搜索法来求解最优化问题的一套优化瞬时单位线的方法.实例研究结果表明,该方法的计算精度高于矩法,能够得到基本反映流域汇流特性的瞬时单位线.在Matlab平台上,通过应用Lobatto积分法对瞬时单位线进行积分来求解S曲线,进而推求时段单位线.这种方法避免了用近似数值公式以及查表带来的误差和不便,提高了计算效率.
[1] 李丽琴,周惠成,顾妍平.流域时变瞬时单位线非线性汇流模型及应用[J].哈尔滨工业大学学报,2009(2):180-182.
[2] 王桂林,伊学农,刘遂庆.遗传算法推求瞬时单位线参数并计算流量过程线[J].环境污染与防治,2003(6):367-369.
[3] 李志龙.新安江模型在资料缺乏的寒区流域的应用研究[D].南京:河海大学,2006.
[4] 雷 璐,宋星原,罗 鹏,等.变动单位线与纳西瞬时单位线在洪水预报中的应用[J].水电能源科学,2011(3):51-53.
[5] 耿鸿江,齐松茹.瞬时单位线的Excel快速算法[J].人民长江,2003(2):6-7.
[6] 包为民.水文预报[M].北京:中国水利水电出版社,2009.
[7] 姚 成,章玉霞,李致家,等.无资料地区水文模拟及相似性分析[J].河海大学学报:自然科学版,2013(2):108-113.
[8] 金菊良,丁 晶,魏一鸣.瞬时单位线的优化估计[J].水力发电学报,2003(1):70-75.
[9] 张 宁.基于遗传算法的试错法推求单位线[J].河南水利与南水北调,2013(4):25-27.
[10]詹道江,叶守泽.工程水文学[M].北京:中国水利水电出版社,2000.
[11]董四辉,周惠成.遗传算法在估计瞬时单位线参数中的应用[J].大连铁道学院学报,2006(4):73-77.
[12]宋叶志.MATLAB数值分析与应用[M].北京:机械工业出版社,2009.
[13]唐发明.基于统计学习理论的支持向量机算法研究[D].武汉:华中科技大学,2005.
[14]张国云.支持向量机算法及其应用研究[D].长沙:湖南大学,2006.
