基于MSC.Marc软件的面板堆石坝静力分析
2014-10-21冯龙龙苏晓丽
冯龙龙 苏晓丽 李 星
(1.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098;2.河海大学 水资源高效利用与工程安全国家工程研究中心,南京 210098;3.河海大学 水利水电学院,南京 210098)
混凝土面板堆石坝是由防渗面板,防渗接地结构以及坝体堆石体组成的混合结构,由于混凝土面板堆石坝具有工程量小、安全、经济、施工方便和适应性好的特点[1],所以它在实际工程中得到广泛的应用.随着技术的发展和设计经验的积累,面板堆石坝的设计高度已经突破了200m,如水布垭水电站的坝高超过了230m.由于坝高的增加,使得坝体的应力和变形变得比较复杂.因此,在设计混凝土面板堆石坝时,对其进行应力和变形分析是十分重要的.本文计算时以某高面板堆石坝为例,利用Marc软件的非线性求解功能进行应力和变形分析,给出其相应的变化规律.
1 有限元计算原理
非线性有限元按位移模式求解的平衡方程为
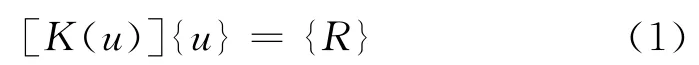
式中,[K(u)]为劲度矩阵,{u}为节点位移列阵,{R}为节点荷载列阵.
本次计算采用中点增量法[2]求解非线性方程组.坝的填筑顺序把自重荷载分为若干级,配合荷载分级进行有限元网格划分.中点增量法把每级自重荷载称为荷载增量,记为{ΔR},如果第i级为{ΔR}i,先根据上一级荷载计算末的{σ}i-1确定弹性常数 Ei-1和νi-1,并组成劲度矩阵[K]i-1,在结构中施加本级荷载增量的一半{ΔR}i/2,用式(2)求得位移增量:
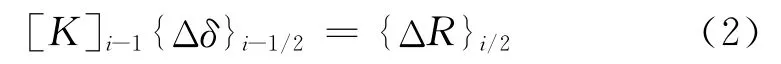
再计算应力与应变增量,叠加到上次计算的应变与应力上,由此得到本级计算的中点应变{ε}i-1/2,然后可以得到弹性常数Ei-1/2和νi-1/2.再用式(3)求本级全荷载发生的位移增量:

最后计算本级的应变与应力增量,累加到上一级终了的应变与应力上,即为本级的应变与应力,坝体上游面的水压力按照蓄水顺序分级加荷.
2 堆石体的本构关系以及在Marc中的实现
2.1 堆石体的本构模型
堆石体的本构关系表达了堆石体应力应变之间的关系,它无疑对应力应变的计算结果起决定性的作用[3],因而采用恰当的本构模型对面板堆石坝应力变形分析是至关重要的.堆石料是非线性材料,根据三轴实验,邓肯-张(E-B)模型能够较好地反映土体材料应力应变的非线性,因此选择邓肯-张(E-B)模型作为堆石料、垫层和过渡料等的本构模型.该本构模型的基本原理[4]为

式中,Rf为破坏比;Pa为大气压力;K、Kb、m、n为试验常数;S为剪应力水平,反映材料强度的发挥程度,S=,(σ1-σ3)f为破坏时的偏应力,由摩尔-库伦破坏准则得:

2.2 在Marc软件中的实现
Marc软件作为大型有限元商业计算软件之一,与其它软件相比,具有能够快速求解高度非线性问题的优点.但是,它不包含工程中常用的邓肯-张(E-B)非线性弹性模型,这严重影响了它在坝工领域中的使用.本文利用 Marc软件提供二次开发功能[5],把通过实验得到的参数利用Fortran语言编写子程序,利用Marc子程序来实现邓肯-张非线性弹性模型的应用,然后利用生死单元技术进行分级加载,以进行坝体施工和蓄水的模拟.
3 面板堆石坝实例分析
3.1 工程概况
某水库工程位于河南省境内,它的开发任务主要是以防洪、供水为主,同时考虑发电和改善生态环境,并进一步完善黄河下游调水调沙运行条件.该工程为混凝土面板堆石坝,设计坝高124.0m,坝顶高程288.5m,顶部设防浪墙,其高度为1.2m,坝顶总长为481.0m,宽为10.0m,设计时上游采用1∶1.5的坡率,下游的为1∶1.6.坝体主要由主堆石区、次堆石区、混凝土面板和防渗墙等几部分组成,主堆石区与次堆石区分界线为坝轴线向下游1∶0.6.根据面板坝规范要求,100m以上的坝面板上游面下部设有上游铺盖区及盖重区,上游铺盖的顶高程,取为坝体高度的35%,即顶部高程在200.00m,最大高度为35 m;在周边缝下设小料区(特殊垫层);下游坡面为大块石护坡.
3.2 有限元模型及其计算参数
考虑坝体分区、施工程序及加载过程,并考虑到防渗墙的连接型式,对坝体及坝基进行剖分,建立三维有限元模型如图1所示,总共剖分9 862个单元,11 489个结点.

图1 有限元计算模型
混凝土面板、趾板、连接板等在达到破坏强度之前线性关系一般较好,故按线弹性材料处理,参数见表1.
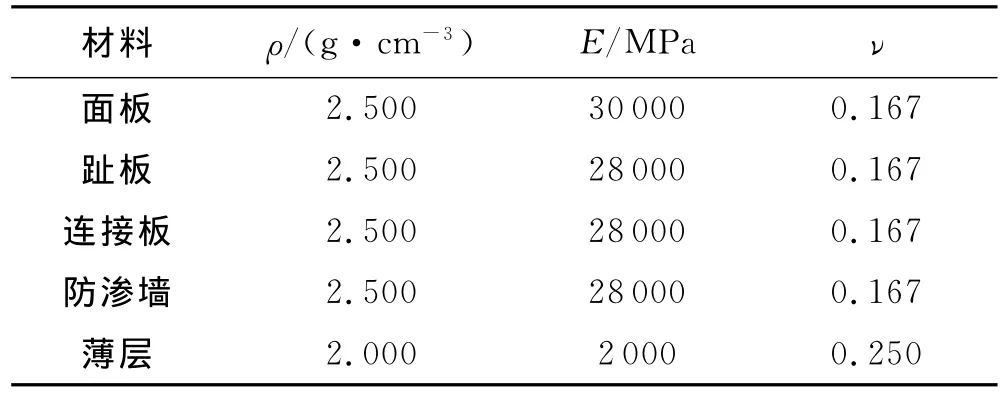
表1 面板堆石坝的弹性材料参数
面板堆石坝中主堆石料、次堆石料、粘土夹层和过渡石料等按照非线性弹性材料进行模拟,计算使用的参数见表2.
荷载加载时,利用Marc软件提供的生死单元功能实现分级加载来模拟面板堆石坝的浇筑过程以及蓄水期的情况.按照面板堆石坝施工进度和蓄水计划,先后将荷载分为24级模拟.
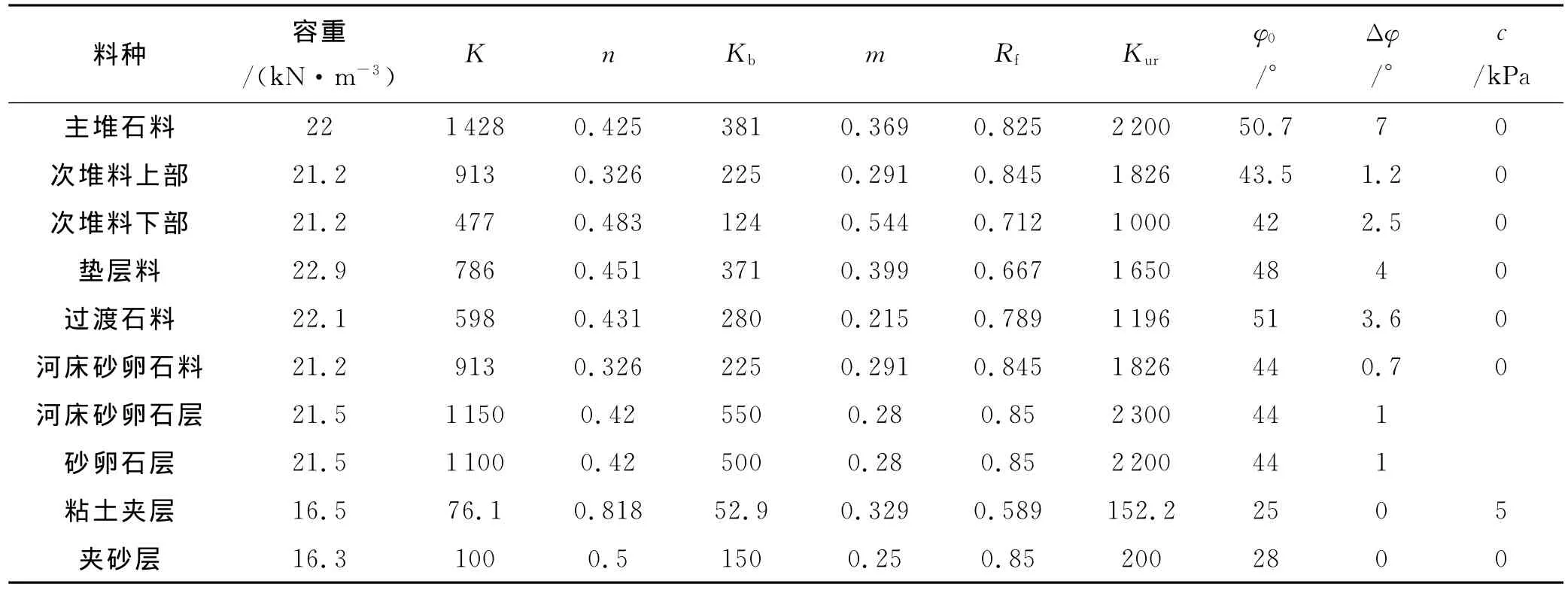
表2 面板堆石坝的邓肯-张模型(E-B)参数
3.3 计算结果分析
分析计算结果时,取3个剖面1、2、3(如图2所示)进行分析,由于篇幅有限,文中只给出2号剖面的等值线图,其它剖面的极值列入相应的表中.计算时选取的坐标方向:x向为顺河向,y方向为坝高方向,向上为正,z轴为坝轴线方向,从左向右;应力按照土力学的习惯,以压应力为正,拉应力为负.

图2 剖面示意图
3.3.1 坝体应力和位移分析
图3为竣工期堆石体2号断面的应力分布,图4为满蓄期堆石体2号剖面的应力等值线图,表3分别列出了3个剖面的应力极值.
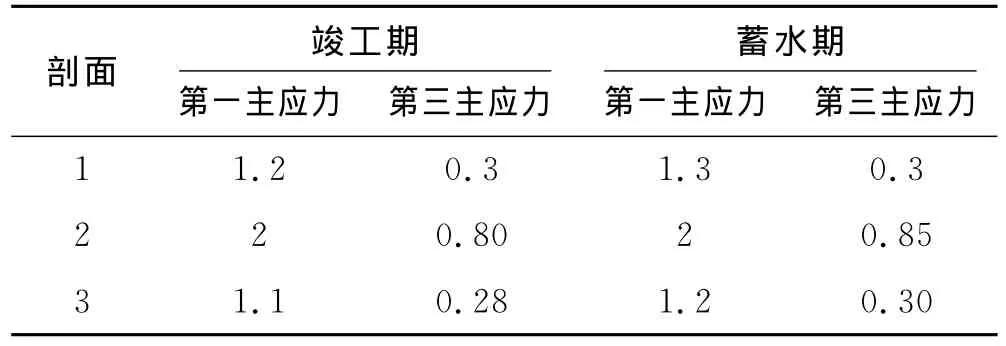
表3 剖面的应力极值统计表 (单位:MPa)

图3 竣工期2号剖面应力等值线图(MPa)
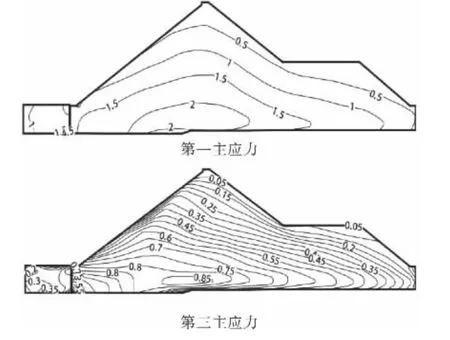
图4 满蓄期2号剖面应力等值线(MPa)
由图3~4和表3可以得到坝体应力分布规律:竣工期坝体主应力等值线与坝坡基本平行,从坝顶向坝基呈逐渐加大的趋势,堆石体应力极大值出现在2号剖面,第一主应力为2MPa,第三主应力为0.80 MPa;蓄水后,受水荷载作用,堆石应力极值增大,所处的位置进一步向上游主堆石区靠近,主堆石区应力较次堆石区应力有所增加,第一主应力最大值为2 MPa,第三主应力最大值为0.85MPa,极值仍然出现在2号剖面.
图5~6分别为2号断面竣工期和满蓄期堆石体的位移等值线图,3个断面的位移极大值列于表4.

图5 竣工期2号剖面位移等值线图(cm)
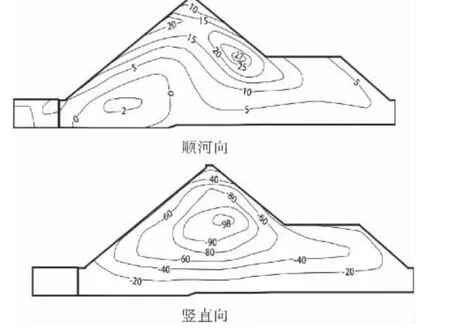
图6 满蓄期2号剖面位移等值线图(cm)

表4 堆石体的位移统计表 (单位:cm)
由图5~6以及表4可以看出:由于堆石体的泊松效应,使得横向剖面上水平位移分布规律基本上是上游堆石区位移指向上游,下游堆石区位移指向下游,这符合竣工期面板堆石坝上下游方向位移分布的一般规律.
1号剖面向上游最大位移为3cm,位于上游侧剖面1/3坝高处;向下游最大位移为7cm,位于下游侧剖面1/3坝高处;最大竖向位移为40cm,位于剖面的1/2坝高处.2号剖面向上游最大位移为9cm,位于上游侧基础覆盖层以上坝体1/4坝高位置,向下游最大位移为23cm,位于基础覆盖层以上坝体1/3坝高位置;最大竖向位移为96cm,位于剖面的1/3坝高处.3号剖面向上游最大位移为3cm,位于上游侧剖面1/3坝高处;向下游最大位移为9cm,位于下游侧剖面1/3坝高处;竖直向位移极值为42cm,位于断面的1/2坝高处.
水库蓄水后,在水荷载的作用下,坝体3个剖面的顺河向位移均有较大变化,但仍然有一定的规律.1号剖面向上游最大位移为1.4cm,位于坝底附近;向下游最大位移为9.3cm,位于下游侧剖面1/3坝高处;竖直向位移极值为40cm,位于剖面的1/2坝高处.2号剖面向上游最大位移为2cm,位于上游堆石区坝底部位置,向下游最大位移为27cm,位于下游次堆石区坝底部附近;最大竖向位移为98cm,位于剖面的1/3坝高处.3号剖面向上游最大位移为1.4cm,位于坝底部附近;向下游最大位移为11cm,位于下游侧剖面1/3坝高处,竖直向位移为43cm,位于剖面的1/2坝高处.
3.3.2 面板应力与变形分析
图7~8分别是竣工期和满蓄期面板的应力图.

图7 竣工期面板应力分布(MPa)

图8 满蓄期面板应力分布(MPa)
由图可知:竣工期,面板顺坡向主要表现为压缩变形,最大压应力为3.8MPa,出现在2号剖面182m高程位置.面板轴向应力与顺坡向应力相比数值较小,基本呈两岸受拉、中间受压分布,最大压应力为0.8MPa,出现在2号剖面180m高程位置,最大拉应力值为1MPa,出现在3号剖面190m高程位置.
蓄水后,面板顺坡向应力仍然以压为主,最大压应力为4.1MPa,出现在2号剖面182m高程位置.但靠近河床两端出现较大的拉应力区,极值为1.8 MPa,出现在面板的最底部.相对于竣工期,轴向应力有所增大,但总体呈两岸面板受拉,中间受压分布,符合轴向应力的一般分布规律:2号剖面高程217m位置轴向压应力最大值为1.5MPa;相对于竣工时面板的拉应力明显增大,而且在靠近河床的两端及两岸周边处会出现较大的拉应力,最大值为2.5MPa.
图9为竣工期面板位移分布等值线图,图10为满蓄期面板位移分布等值线图.
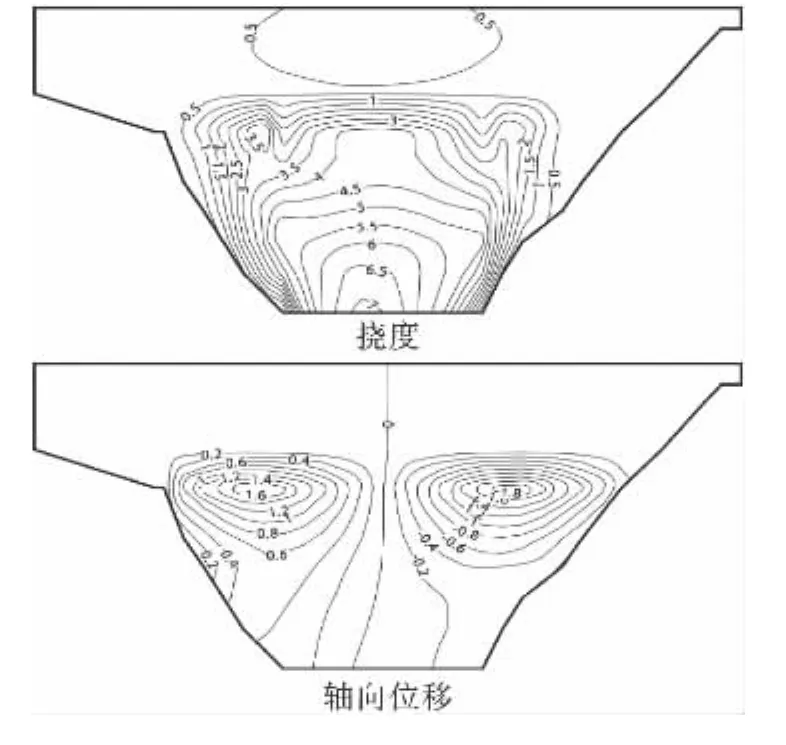
图9 竣工期面板位移等值线图(cm)
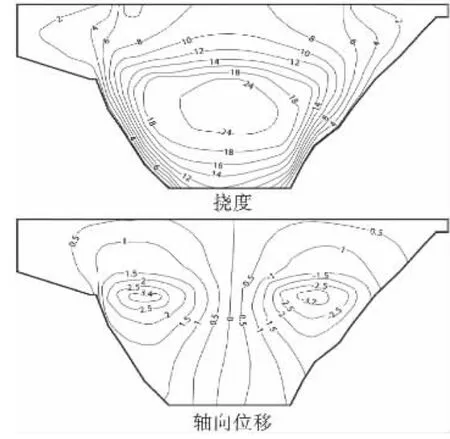
图10 满蓄期面板位移等值线图(cm)
由图9~10可以看出:竣工期,由于已经历了一期面板挡水,因此面板挠度基本指向坝内,位于河床中央的面板底部挠度较大,挠度最大值为7cm;面板在坝轴向上由河谷向中央挤压[6],左岸轴向位移最大值为1.6cm(指向右岸);轴向位移在右岸的最大值为1.8cm,方向指向河床中央.蓄水后,面板变形分布规律较好,面板挠度指向坝内,面板中间区域数值较大,最大值为24cm;面板轴向有进一步由河谷向中央挤压的趋势,轴向位移在左岸最大为3.4cm,右岸为3.7 cm,且分布具有一定的对称性.
4 结 语
本文通过Marc软件提供的子程序功能,利用Fortran语言编写子程序以实现非线性弹性E-B模型在Marc中的应用.根据三维非线性有限元分析可以得出:
1)三维情况下,坝体具有较强的空间效应,河床中央剖面的最大主应力值不在坝基面底部,而位于距离底部有一定距离的位置.
2)由于基础有较深的覆盖层,导致堆石体的最大沉降发生的位置以及面板最大挠度出现的位置相对于修建在基岩上的面板坝位置偏低一些,而且该工程由于次堆石下部参数较低、变形较大,故造成最大值位置偏向下游次堆石下部附近.
3)面板变形分布规律较好,面板挠度指向坝内,坝轴向上由河谷向中央挤压;蓄水后面板应力仍然以压为主,但是在靠近河床两端出现较大的拉应力,在实际工程中应予以重视.
[1] 孔宪京,张 宇,邹德高.高面板堆石坝面板应力分布特性及其规律[J].水利学报,2013,44(6):631-639.
[2] 田 艳,王瑞骏,吕海东.积石峡面板堆石坝应力变形非线性有限元分析[J].水资源与水工程学报,2007,18(5):71-74.
[3] 高 辉,李守义.面板堆石坝非线性有限元应力变形分析[J].西北水资源与水工程,2000,11(4):33-37.
[4] 付国栋,王瑞骏,赵一新.施工期坝面过水面板堆石坝非线性有限元分析[J].水资源与水工程学报,2009,20(6):116-119.
[5] 陈火红,尹伟奇,薛小香.MSC.Marc二次开发指南[M].北京:科学出版社,2004.
[6] 张 峰.深覆盖层面板堆石坝应力变形分析[J].工程地质计算机应用,2012,68(4):30-35.
