碾压混凝土坝施工期徐变温度应力场快速仿真技术

朱优平 李同春 冯树荣 石青春 苏军安

（1.中国水电顾问集团 中南勘测设计研究院，长沙 410014；2.河海大学 水利水电学院，南京 210098）

混凝土坝的徐变温度应力场仿真方法可分为理论解析法和近似法.理论解析法只能用来求解边界条件简单的低维问题，主要用来验证近似方法的可靠性和精确性，对实际工程没有太大的使用价值.近似方法，尤其是有限元法，具有易于适应不规则边界、便于编制通用程序等特点，因此在实际工程中，常常采用有限元法模拟施工期混凝土徐变温度应力场.

碾压混凝土坝通常是分层浇筑的，由于每层混凝土龄期不同，每个浇筑层内的弹性模量和徐变度都不同，因此在仿真计算时，必须对每个浇筑层内都划分网格，而且每个浇筑层内铅垂方向的温度梯度和应力梯度都较大，为了保证计算精度，每层内都需划分密集网格［1］.在层数较多时，因节点太多，方程阶次太高，所需的计算机容量太大.这个问题在碾压混凝土坝的温度应力场仿真中尤为突出，因碾压混凝土浇注采用薄层碾压、连续上升的施工方式，一般每一碾压层厚0.3m，每天可以连续施工5～6层，层面暴露时间为3～4h，间歇期一般为4～5d.尽管碾压混凝土问世初期，人们曾一度认为由于添加了大量粉煤灰并且水泥用量少，应该不会存在温度应力问题，但是后来，碾压混凝土的温度应力就逐渐得到了人们的重视.碾压混凝土坝的施工仓面是大仓面，甚至是通仓的，在施工过程中混凝土受到气温、水温、自身水化热、水管冷却及新老混凝土相互作用等复杂因素下，混凝土的温度变化较大，引起较大的温度变形，当混凝土的变形受到内部或者外部约束时，便会在混凝土内产生较大的温度应力.一般来说，碾压混凝土的抗拉强度低于常态混凝土的抗拉强度，对于高碾压混凝土坝，要把温度应力控制在防止出现裂缝的条件下是非常不容易的，因此温度应力问题成为碾压混凝土坝的核心问题.碾压混凝土坝温度应力问题可以分为施工期仿真和运行期仿真两个部分，大坝在施工期存在的不确定因素远比运行期中多，因此施工期的温度应力问题一直是研究的热点.

综上所述，混凝土温度应力场仿真分析最主要的难点是计算量大、计算速度慢.由于浇筑时间不相同，每个薄层内材料的热学参数和力学参数不一样，如需在计算中较准确地反映每个薄层内的热力学特性，每个薄层内至少要划分两层网格，计算量非常大，甚至现有计算机也无法满足计算需要.尤其是碾压混凝土坝每天可连续施工5～6个薄层，再考虑到环境温度的变化情况，仿真计算时间步长一般是以小时为单位，造成计算次数陡增，计算速度缓慢的问题.

1 冷却水管的模拟

等效算法［2－6］和精细算法［7－11］是有限元模拟水管冷却温度场中最常用的两种方法.等效算法由于是在平均意义上考虑水管作用，将冷却效果看成是一个负的热源，虽然不能反映冷却水温的沿程变化，但是不需要将每根水管都细致地剖分有限元网格，有效地减少了计算工作量.而精细算法却弥补了等效算法中的不足，通过对水管附近大量的网格剖分，以增加计算机时为代价，较细致地模拟混凝土和冷却导热，并能具体反映水管间的温度变化情况.以下简单介绍等效算法和精细算法的基本原理，由于篇幅限制，常规有限元计算温度场和应力场不再赘述.

1.1 等效算法

等效算法是由朱伯芳院士提出来的，其主要思路是把冷却水管当作负热源，在混凝土温度场计算中使水管冷却效果和等效热传导方程建立联系.为了用数值方法求出近似解，可以把只考虑冷却作用而计算的混凝土平均温度作为绝热温升，从而得到如下等效热传导方程

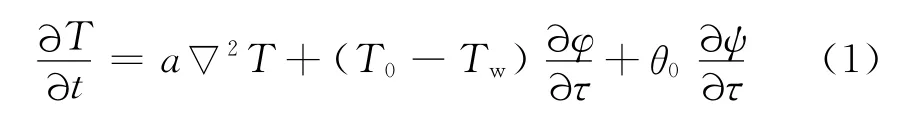
式中，a为导温系数（m2／h）；T0为混凝土温度（℃）；Tw为冷却水温度（℃）；t为时间（d），τ为龄期（d）.

式中，D 为混凝土圆柱体直径（m）；L为水管长度（m）；b为混凝土圆柱体外半径（m）；c为冷却水管外半径（m）；λ为混凝土导热系数（kJ／（m·h·℃））；qw，cw，ρw分别为冷却水的流量（m3／s）、比 热 （kJ／（kg·℃））和密度（kg／m3），θ为绝热温升（℃）.

1.2 精细算法

任取一段含有冷却水管的混凝土，如图1所示.

图1 混凝土中水管冷却示意图

根据傅立叶热传导定律和热量守恒定律可得到水管中水的温度增量：

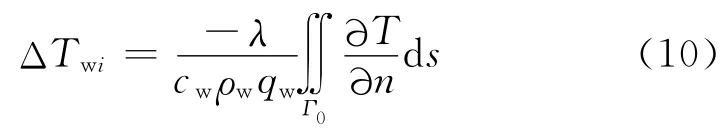
式中变量含义见式（6）.

由于冷却水的入口温度Tw0已知，利用上述公式，对每一根冷却水管沿水流方向可以逐段推求沿程水温.设某根冷却水管共分为m段，则第i水管段内的水温增量ΔTwi为

2 快速仿真计算技术及程序编制

浇筑在基岩上的混凝土，伴随降温过程发生的体积收缩受到基岩的约束，将产生较大的拉应力，如果超过混凝土的抗拉强度将会出现裂缝，产生在基础约束区内的裂缝极易发展成贯穿性裂缝，严重影响混凝土结构的使用性能.相对来说，远离基础约束区因其拉应力区域较小，产生的裂缝相对基础约束区的危害性要小一些，因此，在“无坝不裂”的现状下，严防基础约束区出现裂缝应该是防裂工作的重中之重，在温控仿真计算中，也应着重研究基础约束区的温度和应力变化过程，并努力提高其计算精度.碾压混凝土坝因其施工特点，计算量较大，在现有计算机条件下很难在整体规模下精细地仿真出大坝的温度场和应力场.为了能够同时考虑仿真计算量和计算精度，本文提出在大坝强约束区使用水管精细算法计算，而在其他区域使用等效算法计算的快速仿真技术.其计算思路说明如下：

1）按照大坝的实际的施工组织设计和材料分区设计划分初始网格，尽可能在计算过程中模拟大坝的实际施工过程.

2）对初始网格进行再剖分.在大坝基础约束区等温度变化剧烈的区域精细地划分水管，并记录其在施工过程中的层号.在程序中创建一个计算标示数组，其数组大小与施工层数对应，在通水冷却时，当标示数组值为0时，表示该层按照精细算法进行计算，当标示数组值为1时，表示该层按照等效算法进行计算.

3）在程序中实现等效算法和精细算法的耦合计算.在混凝土通水冷却时，精细算法需要迭代计算沿程水温以确定水管处的计算边界条件，而等效算法是将水管冷却等效成负热源，因此在程序中可以通过修改混凝土绝热温升函数来实现.程序编制时，首先按照精细算法的流程编制出一个计算混凝土水管冷却温度场的程序，在程序中形成单元矩阵时，如果该层是用等效算法计算而且该层水管正在通水冷却，则调用一个修改了混凝土绝热温升函数，如不属于上述情况，则调用混凝土真实的绝热温升函数.

在以上思路的基础上，基于有限元方法基本理论，利用FORTRAN语言编制等效算法和精细算法的耦合计算程序.

3 算 例

3.1 计算模型及计算条件

取某碾压混凝土坝作为算例，建基面高程283 m，坝顶高程295m，混凝土坝浇筑层厚3m，间歇时间为5d，水管间距1.5m×1.5m，浇筑后立即通水40 d，前20d通水流量63.84m3／d，后20d通水流量减半，通水温度17℃，通水方向每天变换一次，碾压混凝土在夏季施工，并未采用任何预冷措施.在高程283～286m的基础约束范围内使用精细算法计算，在高程286～295m范围内使用等效算计算，其计算模型如图2所示，共划分13 318个节点，11 312个单元，并在基础约束区精细剖分了14根水管.

图2 计算网格

气温T（℃）根据当地多年气象观测资料拟合成余弦曲线：

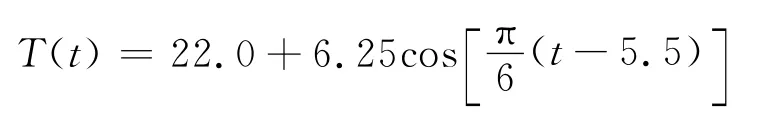
地基温度定为气温的平均值；混凝土的初温取为混凝土入仓温度.与环境接触的地基取为第三类边界条件，离坝体较远的地基取为第二类边界条件.坝体上的边界又分为3种情况：与空气接触的坝体取为第三类边界条件；横缝面侧的边界取为第二类边界条件；在坝体高程295m处，未浇筑上一层时取第二类边界条件，浇筑完上一层后取第一类边界条件，应力计算边界条件按常规取，地基和混凝土的热力学参数见表1.

表1 地基和混凝土的热力学性能指标

混凝土的徐变和自身体积收缩对结构应力仿真计算结果影响较大，必须予以考虑，在本例中，徐变度和收缩应变通过室内实验资料拟合，

3.2 计算结果分析

图3～4是坝轴线中面（垂直水管方向）的温度和应力计算成果.坝体约束区剖分了两层冷却水管网格，精细算法细致地反映了水管附近的温度梯度变化较大的特点，在温度和应力等值线图中，水管附近的等值线较密集，同时每根水管不同的水管截面处，其温度梯度变化在数值上是不同的，进一步说明了精细算法能够反映冷却水的沿程水温变化.而在非基础约束区，因其使用的是等效算法计算，与常规的温度场计算方法相比，等效算法可以看作将冷却效果叠加到混凝土的绝热温升上，因此用较小的计算代价得到混凝土的温度场和应力场，其在非基础约束区是满足工程需要的.

图3 坝轴线中面第30d时温度等值线图（单位：℃）

图4 坝轴线中面第30d时第一主应力等值线（单位：MPa）

此次仿真计算，模拟了坝体施工期分层浇筑，在坝体浇筑至第30d时，混凝土浇筑时间较晚，层面散热和水管冷却还未能发挥作用，在气温和早期混凝土较大水化热作用下，混凝土的温度值会呈现大温升现象，但此时混凝土早期弹性模量较低，因此虽然有较大的温升膨胀，但其产生的压应力不大，坝体上层温度达到30℃，压应力仅为0.2MPa.而坝体基础约束区，因浇筑时间较早，冷却水管的削峰降温作用已充分发挥出来，温度基本控制在24～27℃，降温收缩虽受到地基的强约束，但产生的最大拉应力也仅为0.8 MPa.

4 结 论

基础约束区属于坝体强约束区，该部位长期存在拉应力，产生的裂缝极易发展成危害很大的基础贯穿性裂缝，因此基础约束区的温度和应力变化规律是工程界关心的重点.碾压混凝土坝因其施工特点，在现有计算机条件下很难在整体范围内精细地仿真出大坝的温度场和应力场.基于目前的计算硬件水平和计算方法的限制，为了能够同时考虑仿真计算量和计算精度，本文提出在大坝强约束区使用水管精细算法计算，而在其他区域使用等效算法计算，快速仿真碾压混凝土坝徐变温度应力场.利用自编程序对工程实例进行计算，验证了该法的可行性和工程使用价值.

［1］ 朱伯芳.大体积混凝土温度应力与温度控制［M］.北京：中国电力出版社，1998.

［2］ 朱伯芳.有内部热源的大块混凝土用埋设水管冷却的降温计算［J］.水利学报，1997（4）：87－106.

［3］ 朱伯芳，蔡建波.混凝土坝水管冷却效果的有限元分析［J］.水利学报，1985（4）：27－36.

［4］ 朱伯芳.大体积混凝土非金属水管冷却效果的降温计算［J］.水利发电，1996（12）：26－29.

［5］ 朱伯芳.考虑水管冷却效果的混凝土等效热传导方程［J］.水利学报，1991（3）：28－34.

［6］ 朱伯芳.考虑外界温度影响的水管冷却等效热传导方程［J］.水利学报，2003（3）：49－54.

［7］ 朱岳明，徐之青，贺金仁，等.混凝土水管冷却温度场的计算方法［J］.长江科学院院报，2003，20（2）：19－22.

［8］ 朱岳明，张建斌.碾压混凝土坝高温期连续施工采用冷却水管进行温控的研究［J］.水利学报，2002（11）：55－59.

［9］ 黄达海，杨生虎.碾压混凝土上下层结合面上初始温度赋值方法研究［J］.水力发电学报，1999（3）：34－38.

［10］黄淑萍，胡 平，岳耀真.观音阁水库碾压混凝土大坝温度应力仿真计算研究［J］.水力发电，1996（7）：40－45.

［11］刘光廷，麦家煊，张国新.溪柄碾压混凝土薄拱坝的研究［J］.水力发电学报，1997（2）：19－28.