谈谈探究实验中的数据作图与图像分析
2014-10-21叶鹏松
叶鹏松
(苏州市工业园区莲花学校,江苏 苏州 215123)
数据作图和图像分析是科学研究的重要方法,它不仅可以用图示的方式直观地展示测量的结果,而且还可以清晰地揭示出各个变量之间的变化关系与变化趋势,因此在各类科学研究中有着非常广泛的应用.然而现行的初高中科学类教材却对此缺乏系统介绍,以至于许多重要实验规律的获取过程被形式化或过分简约化.[1]这既不利于学生科学掌握数据作图的基本方法与规范,也不利于培养学生必要的数据图形分析能力,在一定程度上就制约了学生综合探究能力与素养的提升.
随着探究性实验活动在中学开展的不断深入,笔者认为很有必要就这一方法的科学应用作一探讨.下面笔者将结合中学物理教学的常见案例,就探究性实验中的数据作图与图像分析及其应用与同行们作一分析、交流.
1 作图规范
表1所示的是探究弹簧长度与所受拉力关系时获得的实验数据.

表1
若以图示的形式展示这些测量结果,一般可遵循以下的方法和步骤.
(1)在坐标纸上建立直角坐标系,水平轴画于纸的底端,纵轴画于纸的左端,图应尽可能大一些,大的图有利于提高作图的精确度.
(2)明确自变量和应变量,并标于相应的坐标轴上.自变量是指那些实验中数值可以直接设定或加以控制的变量.本实验中自变量是指拉力F;应变量是指那些实验中数值无法直接加以控制的变量,它可以看作是自变量变化的结果.本实验中的应变量是指弹簧长度L.根据约定,自变量应画于水平轴,应变量应画于竖直轴.另外,对于时间这一变量而言,人们总是将它画于水平轴上.
(3)确定每个变量变化的范围,选择合适的比例标度,并标于相应的坐标轴上.
(4)标明每个坐标轴所代表的变量名称及其单位符号.
(5)为图表加上标题,表明图表反映的内容.
(6)在坐标纸上精确标定各个数据点,用圆点或小叉(×)标记各个数据点的位置,绘制出一条最适合的光滑图线,让它尽可能地通过或靠近所有的数据点.图线可能是直线,也可能是曲线.本实验中为一条直线.如果绘制正确的话,未在图线上的少量数据点几乎会等量地分布在图线的两侧.如此的图线有利于我们减小各种测量带来的偶然误差.这种画图的方法常称为描点法.注意切不可以简单地用线段直接将各个数据点分别相连.完成(1)至(4)步骤所得的图形如图1(a)所示,完成(5)至(6)步骤所得的图形如图1(b)所示,它直观地展示出弹簧长度随拉力增大而均匀增加的线性关系.
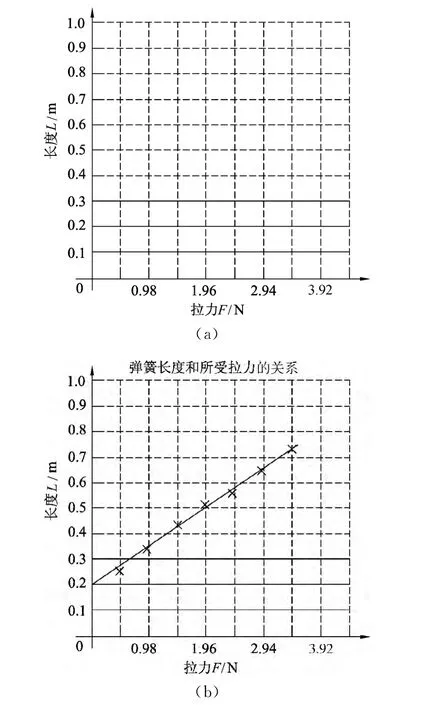
图1
2 图像分析
绘制图像不是实验探究的最终目的,探究的目的是通过绘制图像,找出或发现隐含于其中的变量间的变化关系,就像开普勒从第谷的观测数据中发现开普勒三定律一样.下面结合图1(b)再谈谈图像分析的一般方法和步骤.
2.1 直线方程的推导
图1(b)显示了弹簧长度与所受拉力之间具有线性关系.根据数学知识,它应符合方程y=ax+b(其中a为直线斜率,b为纵轴截距),那么如何推导这一线性方程的具体表达式呢?以下是常用的方法和步骤.
(1)在直线上选取距离足够大的两个点.
(2)分别求出这两点之间的水平变化量和竖直变化量.
(4)找出直线在纵轴上的截距b.
(5)用实际变量的符号和计算结果代换直线方程y=ax+b.
对于本实验,图1(b)中的各变量数据关系方程可表示为L=0.15 F+0.20.由于这类关系表达式来自实验,所以又常被称作经验公式.
(6)阐述图像的斜率与截距的含义.图像中的斜率a=0.15m/N,它表明在实验范围内,每增加1N的拉力,该弹簧就增加0.15m的伸长;图像中纵轴的截距为0.20m,这是F=0时弹簧的长度,就是该弹簧的初始长度.完成上述步骤后,所作对应的图像如图2所示.
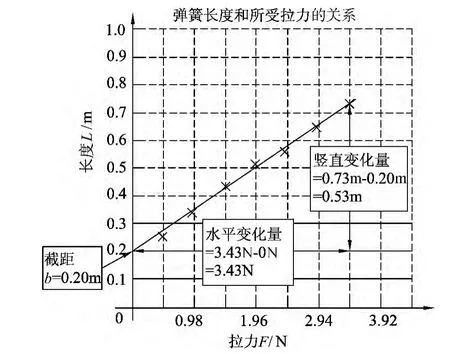
图2
2.2 内插法与外推法
结合所绘图像,可以非常方便地由一个变量的数值推测出另一变量的数值.例如,从图1中我们既可以找出当弹簧的长度L=0.40m时,它所受的拉力F=1.30N;又可以得出当弹簧所受的拉力F=3.92N时,弹簧的长度L=0.80m,如图3所示.但2者在方法上略有不同,前者是在实验测量范围内寻找另一变量的数值,它推算出的结果可靠,这种方法称为内插法.而后者是在实验测量范围以外,寻找另一变量的数值,结果有时不可靠,这种方法称为外推法.很显然,如果拉力取值太大,会超出弹簧所能承受的弹性限度,这一线性关系可能就不再成立,因此图中的这一部分用虚线加以表示,见图3所示.
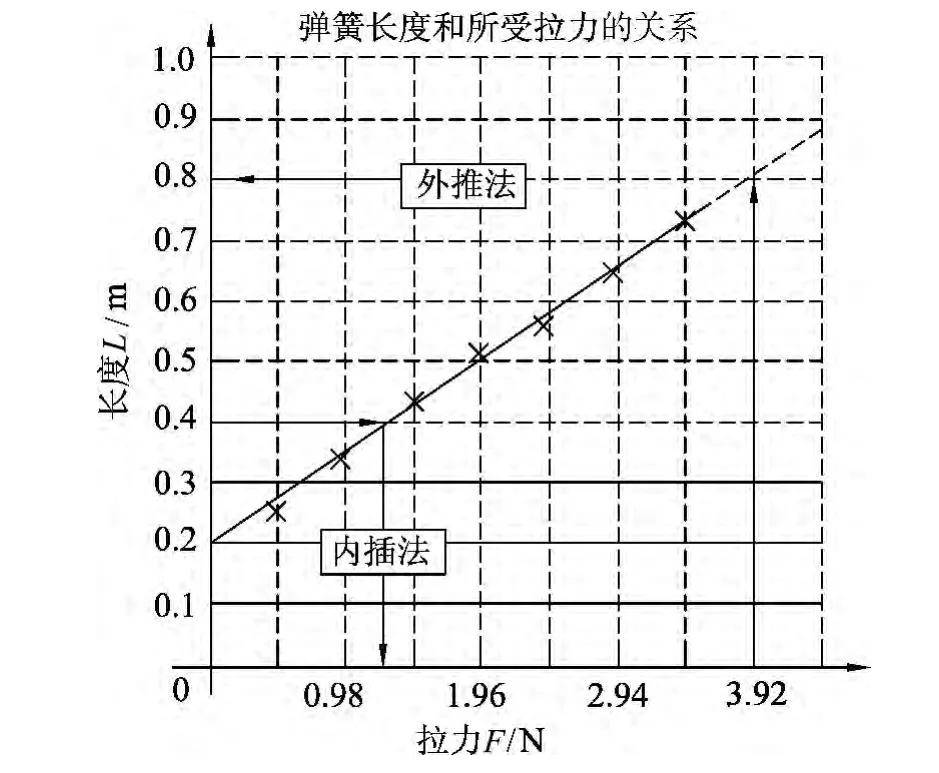
图3
当然,内插法与外推法也可结合所导出的直线方程加以应用,这时只需将某一变量的数值代入方程,即可求出另一变量.
2.3 对其他线型的分析
除了简单的线型关系外,物理探究实验中还会遇到其他许多较为复杂的函数关系.例如,理想气体等温变化时,气体压强与体积的反比关系;自由落体下落高度与下落时间的平方关系;单摆做简谐运动时周期与摆长平方根关系等等,它们的关系图线分别如图4(a)、(c)、(e)所示.对于这些关系图线又如何加以分析呢?通常可采用化曲为直的方法,即通过坐标变换,将曲线图转换为直线图来加以分析处理,具体过程如图4(b)、(d)、(f)所示.
以上列举的各种关系,实质都是一种幂函数关系,指数分别为-1,2,.有时若不能明确指数的数值,我们还可以采用对数坐标来进行分析.
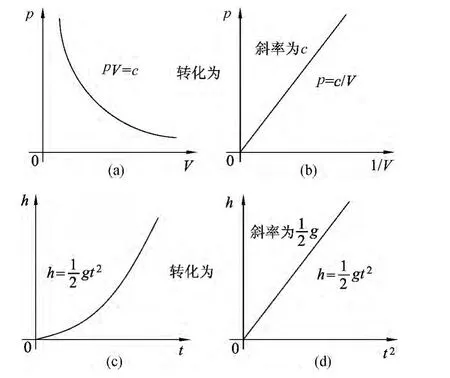
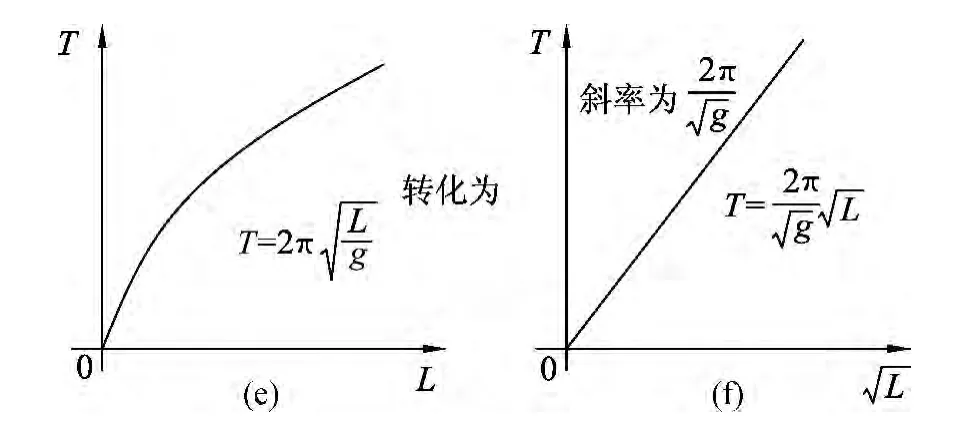
图4
例如,假设球的体积与球的半径之间满足V=krn,式中k为比例系数,n为指数.若要确定k和n的数值,可先将它两边同时取对数,得出lgV=nlgr+lgk;再作出lgV对lgr的直线图,其结果如图5所示.最后再根据图形推得它的斜率n,根据截距推出k.这样,我们就可由实验推导出球的体积公式,并可用它来检验理论公式的正确性.
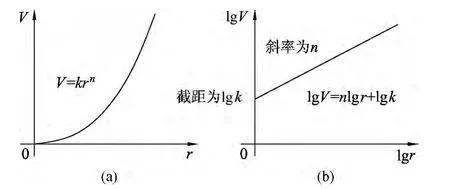
图5
3 计算机软件在作图与图像分析中的应用
以上介绍的是一些探究性实验中作图及图像分析的基本方法和过程,其实,随着信息技术的发展与普及,有很多计算机软件可以帮助我们自动完成这一过程.例如,微软的Excel软件就是一个功能强大的图表制作与分析软件,它不仅可以帮我们轻松完成各种图形的制作,而且还能运用统计分析功能找出最合适的图线.灵活地运用这些软件,不仅可以提高图形制作与分析的工作效率,而且更为重要的是,还能够提高图形分析与结果的准确性.
下面以学生探究单摆做简谐运动时周期T与摆长L关系时,[2]获得的一组实验数据为例(见表2所示),谈谈Excel在这方面应用的基本方法及其过程.
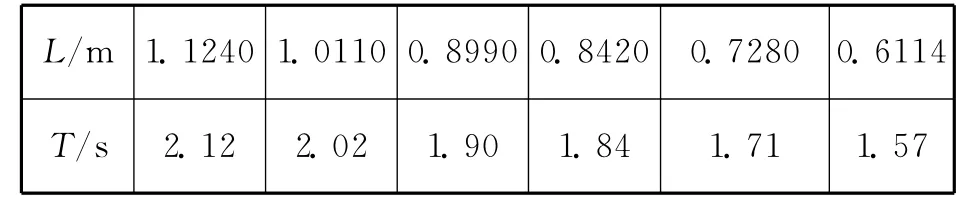
表2
启动工作表,在各标题列输入相应实验数据.
(1)数据预处理.
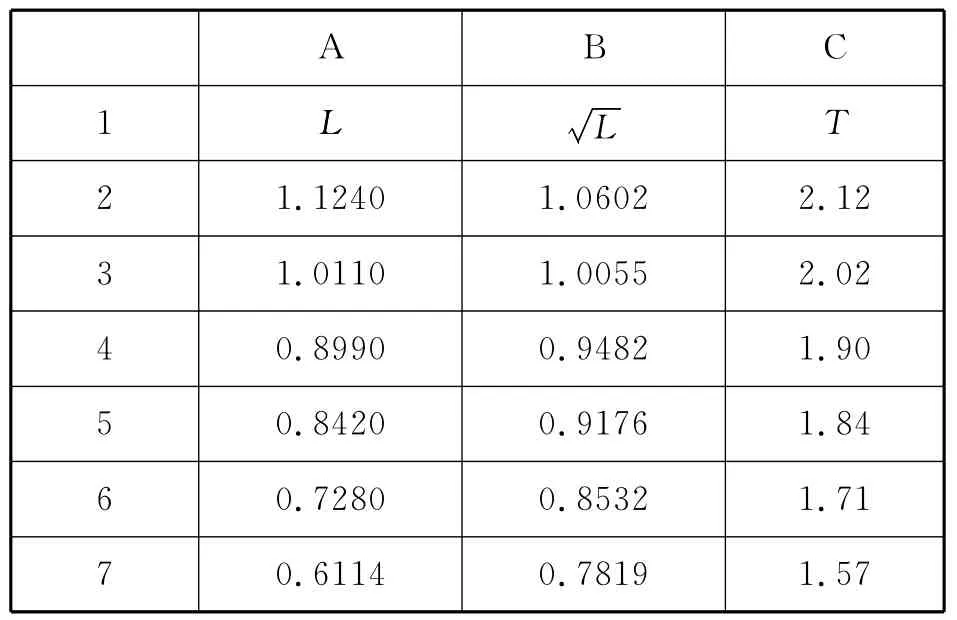
表3
(2)绘制图像.
① 选中作图的数据区域(B2∶C7),在工具栏中按一下作图按钮创建图形.
② 在图表类型中选择散点图.
③ 在标题框中输入图表标题.
④ 在数值(x)轴框内输入自变量名称和单位符号.
⑤ 在数值(y)轴框内输入应变量名称和单位符号.
⑥ 点击完成按钮.
(3)数据拟合.
① 选中所作图表,点击菜单栏“图表”按钮,选中“添加趋势线”.也可以在图表区数据散点上按右键,选择“添加趋势线”.
② 在添加趋势线类型中选择“线性”选项.
③ 在添加趋势线选项中选中“设置截距为0”和“显示公式复选框”.
④ 图表区会自动拟合并绘制出最佳直线,并显示出它的方程.
(4)保存工作表.
当完成上述步骤后,保存工作表.得到的单摆简谐运动周期与摆长的关系图如图6所示.
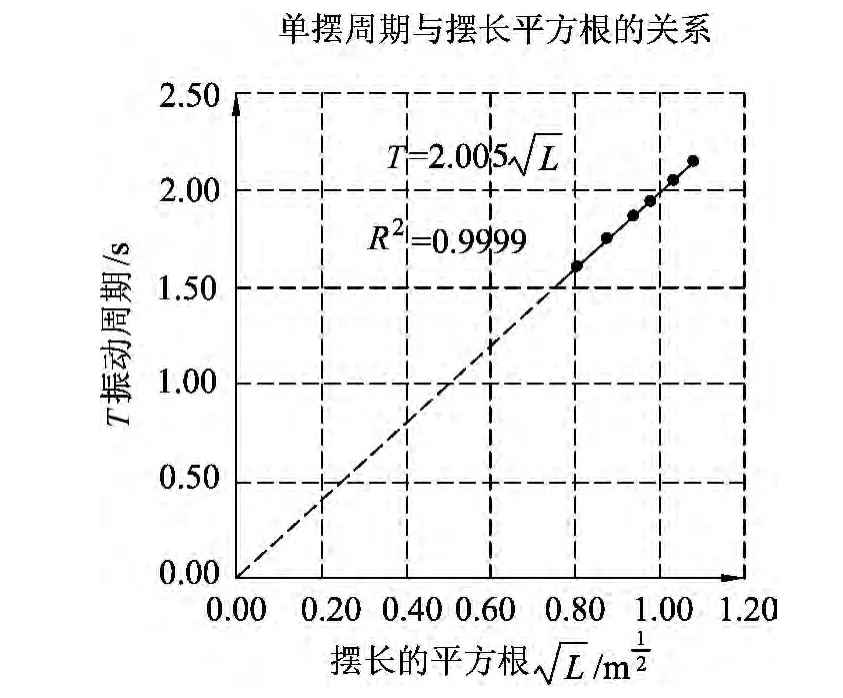
图6
(5)分析方程的斜率和截距.
Excel对这一线性拟合趋势线给出的R2(相关系数的平方)为0.9999,非常接近于1.这也充分说明:在整个实验的摆长变化范围内,单摆的简谐运动周期T与单摆摆长的平方根之间存在正比关系.
显然,这一过程同以往高中物理课本中单纯地测重力加速度的实验相比,更突出了实验探究的科学思想和方法技能.
基于上述思想,笔者还依托综合实践活动课程,开设了“科学探究中实验数据的图表分析”专题学习网站,http:/www.sipxw.cn:8080/dataanalysis/dataanalysis.htm.[3]
上面列举了许多有关数据分析处理的实例,可以有效地指导学生在数据采集的基础上,去自主发现开普勒第三定律、哈勃定律、刹车规律、收尾速度规律、[4]抛体最佳投掷角[5]等一系列实验规律,从而有效地提高学生信息化背景下的探究能力.
除Excel软件外,还有一些小巧的专业软件也可用于探究实验的作图和图像分析,例如Equation Grapher with Regression Analyzer和Graphical analysis都是很不错的数据图像分析软件,尤其是Graphical analysis.2002年笔者在新西兰进修时,就看到许多新西兰的学生在探究实验中,熟练地运用它来处理分析数据,探究实验规律,非常专业,很值得我们国内的教学借鉴.目前该软件还推出了面向移动终端的软件版本,有兴趣的读者可分别到下列网站下载这些软件的试用版:http:/www.mfsoft.com/equationgrapher和http://www.vernier.com/soft/ga.html.
对比国外的物理实验教学,笔者感到国内物理教材在编写时可进一步突出探究实验教学中数据作图与图像分析的系统性介绍,同时加强物理学科与信息技术应用的有机整合,以突出信息化背景下科学探究的时代性和实效性.
1 杨勇诚.巧用Excel软件处理物理实验数据的教学案例[J].物理教师,2013(6):38-40.
3 叶鹏松.科学探究中实验数据的图表分析[J].网络科技时代,2008(130):54-57.
4 叶鹏松,陈刚.收尾速度的实验探究[J].物理教学,2004(8):21-22.
5 叶鹏松.基于Excel的多变量动态控制演示[J].中学物理教学参考,2003(11):53-54.
