基于双向流固耦合的水轮机转轮动态特性研究

李永恒，庞立军



基于双向流固耦合的水轮机转轮动态特性研究

李永恒1,2，庞立军1,2

(1. 水力发电设备国家重点实验室，哈尔滨 150040；2. 哈尔滨大电机研究所，哈尔滨 150040)

由于结构及流固耦合的复杂性，一直很难准确模拟水轮机转轮的动应力状态。利用双向流固耦合的方法，求得了水轮机转轮的动应力，得到了转轮运行中动应力的变化幅值。通过对结果的分析发现转轮应力和变形近似做周期变化，且周期和叶片与导叶个数有关。通过这种方法求出动应力后即可较准确预测转轮疲劳强度，也可对转轮在各个工况下动应力进行模拟，避免机组在转轮动应力较大的工况长期运行。同时对转轮固有频率及振型进行对比研究。相比在空气中，在水压力及离心力载荷作用下，转轮的固有频率下降约1%，这是由于水电机组刚度较强的原因，而在静水中下降较多。

双向流固耦合；转轮动应力；动态特性；水轮机

0 前言

国内外大型水轮发电机组频繁发生转轮在运行过程中出现裂纹的问题，如五强溪、小浪底、二滩、岩滩、大朝山等电站，有些电站甚至发生过在运行中叶片断裂掉落的现象，对机组安全运行构成了威胁，也带来了较大的经济损失。研究表明，由于振动引起的交变应力加上工作介质水的腐蚀，是转轮叶片产生裂纹的主要原因[1]。

水轮机的转轮在运行过程中由于各种原因会引起振动，如导叶与转轮叶片间的相互干扰会诱发振动；叶片出水边的卡门涡脱流会诱发振动；尾水管周期性的涡带会引起尾水管、转轮和轴系的周期振动，流道及转轮的水力不平衡力也会引起机组周期性的振动。

为了研究转轮的应力状态，人们在这方面做了很多努力。有人用单向流固耦合的方法计算了转轮的静应力，有人用试验的方法测得了转轮不同工况的应力，有人研究了载荷的大小对转轮应力的影响,有人先用CFD软件计算出不同时刻作用叶片上的压力,再把这些压力依次施加到叶片上,来看叶片的响应,未考虑流体和固体的耦合。然而由于转轮结构及流固耦合的复杂性，很难准确模拟转轮的应力状态尤其是动应力。工程中常用的方法是先计算出转轮静应力，再根据经验估算一个动应力的幅值，这种方法会有一定的误差，这也是转轮经常出现裂纹的一个原因[2-5]。

本文利用双向流固耦合的方法，考虑了工作介质水对结构转轮的作用，也考虑了转轮的振动、变形对整个流体域的反作用，通过对一个混流式水轮机整个流道进行模拟，求得了转轮应力随时间的变化，得到了转轮的动应力。这样就使得可以在设计阶段较准确的预测转轮的疲劳强度。

转轮振动的大小除了与激振力有关外，还与转轮本身的固有频率有关。现在常用的计算转轮固有频率的方法是先计算出转轮在空气中的频率，再乘以一个下降系数得出转轮在水中的固有频率，实验表明这种方法得到的结果与实际情况有较大误差，因为结构在水中的固有频率与诸多因素有关。本文利用双向流固耦合的方法也分别对转轮在水压力及离心力作用下、静水中、空气中的固有频率及振型进行了对比分析。

1 双向流固耦合计算方法

1.1 流体域模型

水轮机内部的不稳定流动是一个非定常有粘性不可压三维湍流问题。现在常用的湍流模型有K-Epsilon湍流模型系列、K-Omega湍流模型系列、Spalart-Allmaras湍流模型系列、Large-Eddy- Simulation Model湍流模型系列[6]。

基于雷诺平均的N-S方程为：

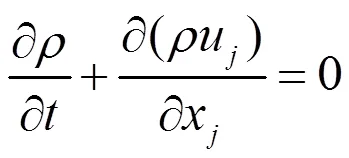
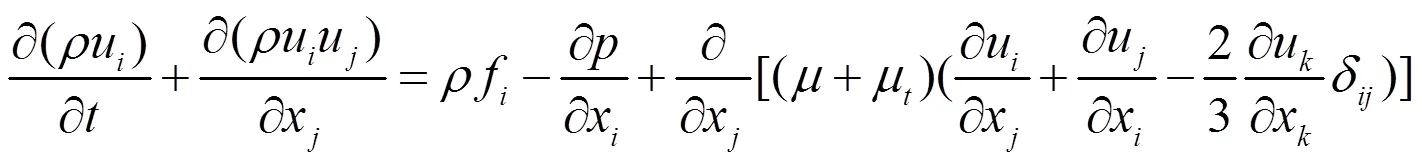
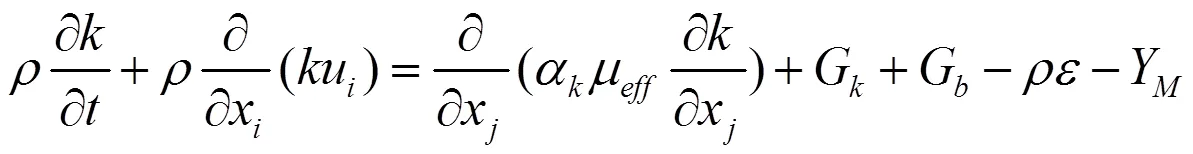
其中，、为流体的密度和静压；，，分别表示坐标分量、速度分量及惯性力分量；为分子粘性系数；μ为湍流粘性系数。

式中：等效粘性系数μ为分子粘性系数和湍流涡粘性系数μ之和：

μμ+μ(5)

G代表由于速度梯度导致的湍动能产生项：

方程中的G是由于浮力产生的湍流动能，在不可压流动中，可忽略；Y代表在可压缩湍流中扩张耗散项，在不可压缩流动中，可忽略。

1.2 结构域模型

弹性体的结构动力学方程为：

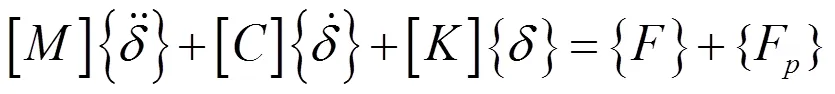
1.3 双向流固耦合求解过程

当一个物理场分析的输入依赖于另一个分析的结果时，这些分析是耦合的。作用在转轮上的压力值依赖于流体的计算结果，同样，在流体压力的作用下转轮出现变形、振动，反过来对流体域又产生影响，这就是双向耦合，又称完全耦合。对于本文研究的对象，转轮是在流体的作用下开始转动的，流体起到一个驱动力作用，流体先动，因此第一步先进行流体域计算。

为了改善水轮机的水力性能，有必要进行双向流固耦合计算，从而设计出即满足水力性能又满足刚强度的优秀转轮叶片，以其最大程度地避免转轮叶片在运行过程中的裂纹产生。图1为一个时间步的计算流程图。

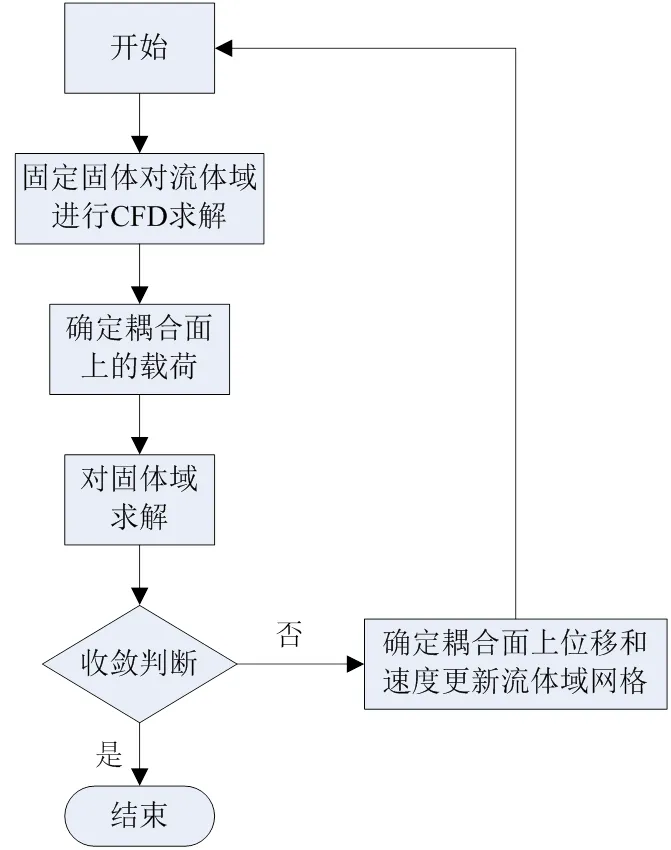
图1 双向流固耦合求解流程

2 转轮动应力及动态特性分析

本文分析转轮动应力及动态特性的几何模型是依据某电站机组的尺寸建立的，机组相关参数见表1。

表1 电站相关参数

2.1 转轮动应力分析

2.1.1 求解模型

为了使分析结果与转轮的实际运行情况接近,能够更准确的得到转轮的动应力及变形,对整个流道进行了模拟。建立的模型包括蜗壳、座环、固定导叶、活动导叶、转轮、导流锥和尾水管，模型如图2所示。

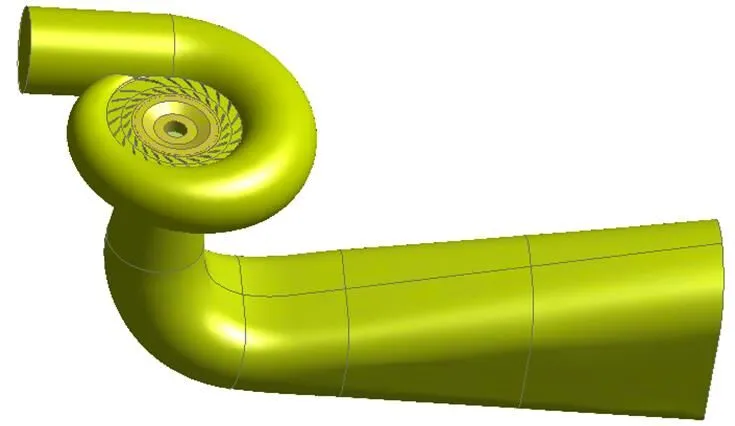
图2 全流道水域中转轮动应力计算模型

2.1.2 求解设置

流体域边界条件设置如下：

（1）入口条件：采用质量入口条件，在蜗壳进口处给入口流量296.4m3/s；

（2）出口条件：采用平均静压出口条件，在尾水管出口处静压为=0MPa；

（3）壁面条件：固体壁面采用无滑移边界条件，近壁区采用标准壁面函数。

对固体计算域，约束转轮与主轴连接法兰面，过流面为流固耦合面。

2.1.3 计算结果分析

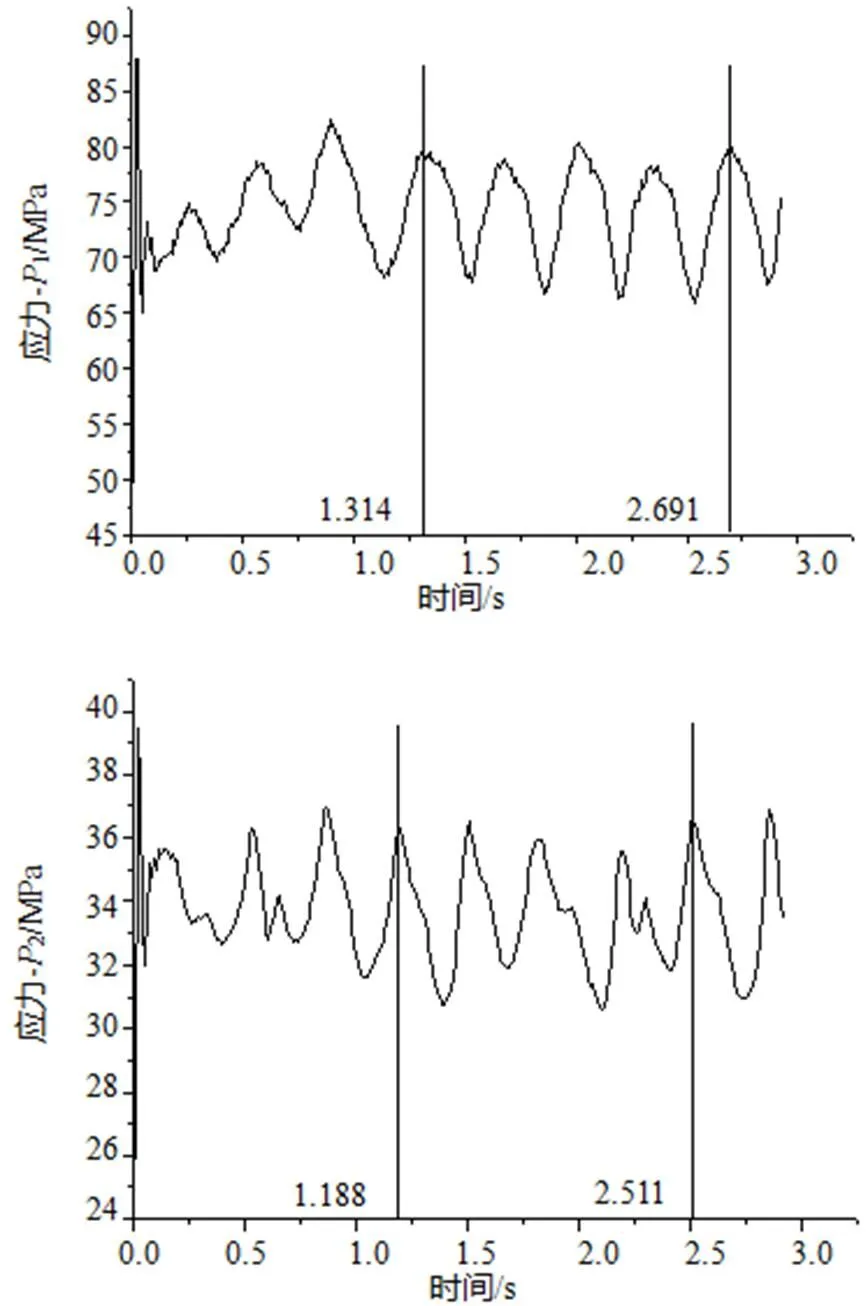
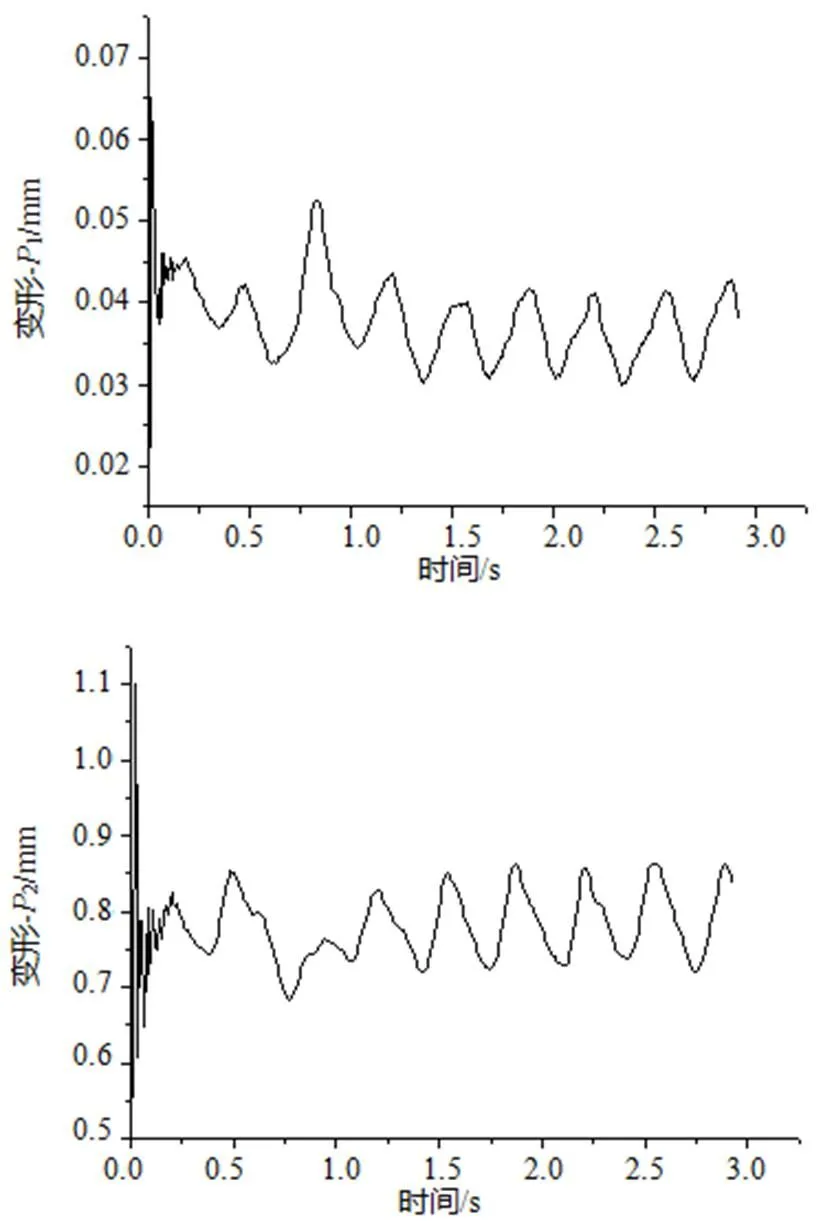
通过计算得到了转轮动应力及变形。分别选叶片进口边与上冠、下环的相交处附件节点1、2和出口边与下环相交处附件节点3。这三个节点的应力及径向变形如图3、图4所示。

从图3和图4可以看出，刚开始时应力及变形幅值变化很大，但很快就相对稳定下来，这是由于开始双向流固耦合迭代前选了以前按稳态计算的一个结果作为初值，也是开始时水对转轮瞬态的冲击造成的，这也说明初值的重要性。

最大应力出现在叶片进口和出口与上冠、下环连接处。在振动相对稳定区域，1、2、3三个节点应力的变化幅值大约分别为14MPa、6MPa、12MPa，静应力也是转轮应力最大的位置，加上工作介质水的腐蚀，这些位置就很容易产生叶片的裂纹，位置和实际中裂纹常出现的位置相同，也验证了结果的可靠性。

从图3、图4可以看出，在振动相对稳定区域，应力和变形近似做周期振动，取应力稳定区域四个周期波动，时间区间分别为：1.314-2.691s、1.188-2.511s、1.27-2.655s，时间长度为1.377s、1.323s、1.385s，转轮旋转一周的时间为0.56s，即在这三个节点，高应力出现的频率分别为转频的1.63,1.69,1.62倍，接近于活动导叶与转轮叶片个数比1.6。

2.2 转轮固有频率及振型分析

研究转轮固有频率及振型时对比分析了以下三种模型：（1）转轮在水压力及离心力作用下；（2）转轮在空气中；（3）转轮在静水中。

2.2.1 模型设置

（1）考虑水压力及离心力作用的模型。模型和求解转轮动应力类似，流体域为全流道，作用在转轮上的水压力通过单向流固耦合方式由CFX求得后直接施加在转轮过流面上，作用在转轮上的水压力如图5所示。约束转轮与主轴连接法兰面。

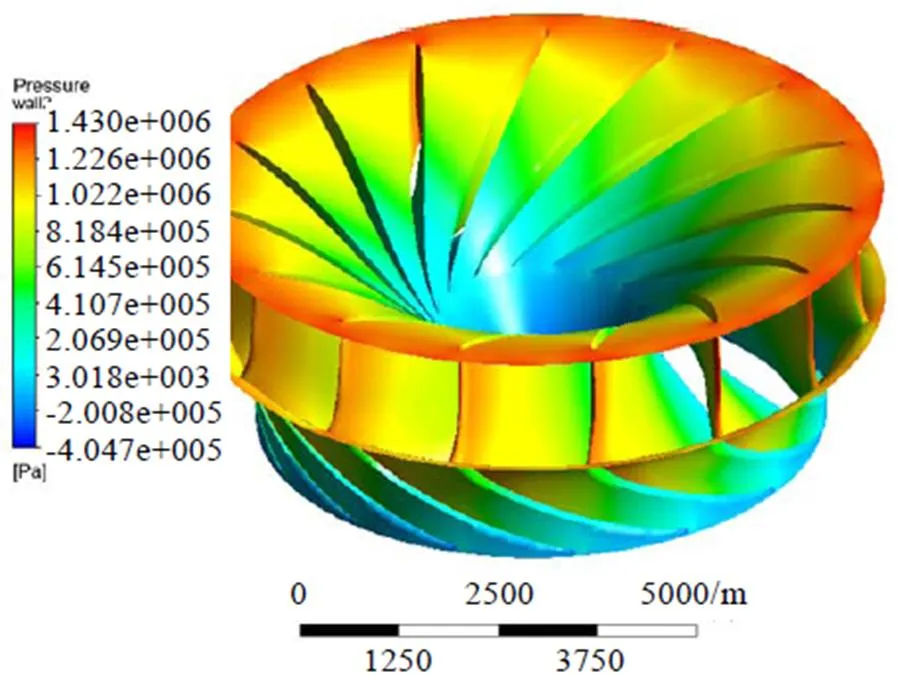
图5 转轮水压力分布图

（2）空气中的模型约束转轮与主轴连接法兰面。

（3）静水中的模型。由于流体域的选取对结构在流体中的固有频率有一定影响[7]，因此，仍选整个流道作为流体域，过流面作为流固耦合面。约束转轮与主轴连接法兰面。

2.2.2 计算结果及分析

列出了三种模型的前几阶计算结果见表2，转轮在静水中的振型如图6所示。

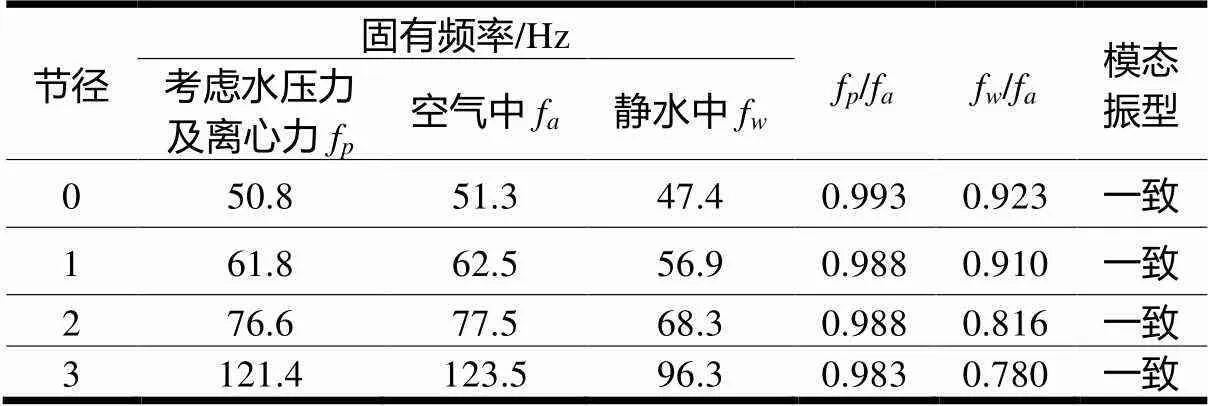
表2 转轮固有频率计算结果

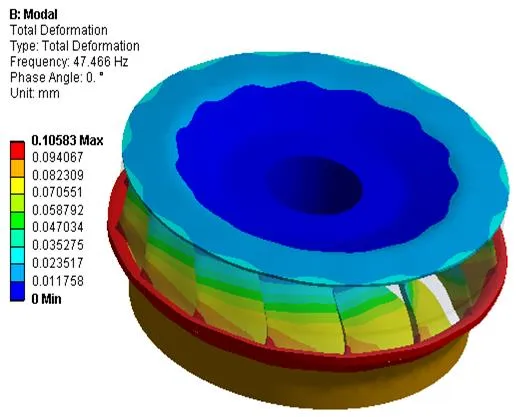
通过对转轮在三种模型下计算结果对比分析可以看出，转轮在同一阶次的振型是一致的；在水压力及离心力作用下转轮的固有频率与空气中相比，下降系数约为1%左右，这是由于对于水电机组而言，部件的结构尺寸相对较大，刚性相对较强，而在静水中的固有频率与空气中相比，下降系数约在10%~20%之间。由于水压力和离心力载荷对转轮固有频率的影响程度非常小，这种微小的影响在工程中可以忽略不计，因此，在求解转轮模态时，只计算转轮在静水中的固有频率和振型就可以满足工程技术的要求。

3 结论

利用双向流固耦合的方法，既考虑工作介质水对转轮的影响，也考虑转轮对流体域的反作用，求得了转轮的动应力及变形随时间的变化。运用这种方法求得转轮动应力后就可以在设计阶段较准确的预测转轮的疲劳强度，最大程度避免转轮裂纹的产生。同时可以对转轮在各个工况运行时的动应力及变形进行模拟，发现转轮在哪些工况下运行时动应力较大，实际运行中能够避免。在运行过程中，转轮的应力和变形近似做周期振动，周期和叶片与导叶个数有关；与在空气中相比，在静水中转轮的固有频率下降较多，且不同阶次下降幅度不同，然而在水压力及离心力作用下转轮的固有频率下降较少，约1%，这是由于水电机组刚度较强的原因，这点在工程中可以忽略，因此，求解转轮模态时，计算转轮在静水中的模态即可。

[1] 于纪幸, 徐抱朴, 孙殿湖, 等. 大朝山水电站水轮机转轮制造和质量分析[J]. 大电机技术, 2004(2): 46-51.

[2] 肖若富, 王正伟, 罗永要. 基于流固耦合的混流式水轮机转轮静应力特性分析[J]. 水力发电学报, 2007, 26(3)：120-124.

[3] 肖若富, 王福军, 桂中华. 混流式水轮机叶片疲劳裂纹分析及其改进方案[J]. 水利学报, 2011, 42(8): 970-974.

[4] 吴彤峰, 黄文, 毛汉领. 混流式机组转轮的有限元计算及裂纹成因分析[J]. 广西科学院学报, 1999,(3): 129-131.

[5] 郑小波, 罗兴锜, 郭鹏程, 基于CFD分析的轴流式叶片动应力问题研究[J]. 水力发电学报, 2009, 28(3): 187-192.

[6] Albert Ruprecht, Thomas Helmrich, Thomas Aschenbrenner, Ahomas Acherer. Simulation of Vortex Rope in a Turbine Draft Tube[A]. Proceedings of the XXISTIAHR Symposium on Hydraulic Machinery and Systems[C]. Lausanne: 2002, 9-12.

[7] 庞立军. 水轮机活动导叶水下模态分析[J]. 东方电气评论，2010, 24(93): 53-56.

Dynamic Characteristic Analysis of Turbine Runner by Two-way Staggered Fluid-structure Coupling Method

LI Yongheng1,2, PANG Lijun1,2

(1. State Key Laboratory of Hydropower Equipment, Harbin 150040, China;2. Harbin Institute of Large Electrical Machinery, Harbin 150040, China)

Due to the complexity of structure and fluid-structure coupling, it is difficult to accurately simulate the stress state of the turbine runner. The dynamic stress of the turbine runner in running were obtained by using the two-way staggered fluid-structure coupling method. By analyzing the results, it was found that the stress of the turbine runner was approximate periodicity and the periodicity has something to do with the number of guide vanes and the blades. After acquiring the dynamic stress, the fatigue strength could be accurately predicted, and the stress states under all working condition could be simulated. Meanwhile, the nature frequency and the vibration mode of the turbine runner were studied. Because of the greater structural stiffness of the hydroelectric generating set, the nature frequency under the water pressure and the centrifugal load was less about 1% than that in the air, and the decrease amplitude under still water had a more significant.

two-way staggered fluid-structure coupling method; dynamic stress of turbine runner; dynamic characteristic; hydraulic turbine

TK730.3+23

A

1000-3983(2014)02-0053-05

国家科技支撑计划（2012BAF12B16-1）

2013-02-10

李永恒（1983-），男，2009年7月毕业于西安交通大学流体机械及工程专业，研究方向为流体机械结构强度与振动，工程师。

审稿人：吕桂萍