基于遗传算法的水轮机调速系统PID参数整定

龙永辉，肖康乐



基于遗传算法的水轮机调速系统PID参数整定

龙永辉1，肖康乐2

（1. 中国石化集团西南石油局重庆钻井公司，重庆400042；2. 江苏沙河抽水蓄能发电有限公司，江苏溧阳213300）

本文结合实际案例研究了遗传算法在水轮机调速系统PID正定控制过程中的应用，研究结果指出：PID调节当前比较流行的调节方式，以往常用的水轮机调速系统PID的调节参数主要是靠经验通过人工试凑的方法进行设定的，缺乏理论性指导；本文通过使用遗传算法与PID控制参数的相互结合，对其中的水轮机调速参数，，K进行了不同程度的优化，取得了良好的实验结果。

水轮机；PID调节；遗传算法

0 前言

水轮机调节速度的PID控制系统算法比较简单，实用性比较好，在实际控制运行过程中具有较高的稳定性。本文所研究的主要内容就是基于遗传算法的水轮机调速系统的PID参数正定的研究分析。下面简单的对遗传算法和水轮机的调速进行简单的介绍。本文所提高的遗传算法是由美国芝加哥大学的霍兰德教授在上个世纪六十年代提出来的，这种算法以遗传机制和生物进化理论为基础并进行随机搜索的优化算法。水轮机调速控制系统中的PID算法通过引入优化参数形成的编码群体，并结合遗传算法中的复制、交叉以及变异，对个体进行适配值的筛选，如果适配值较高，剩下的个体将会组成新的个体，继承了上一代的信息，同时又是对上一代群体的优化，如此循环往复，最终得到最优解。其次，本文所提到的水轮机调速系统原理主要是由用来检测机组转速功率的检测元件将其检测结果转化成一定的控制信号通过PID调节来控制执行机构来控制接力器的行程，达到控制导叶开度的目的，从而控制通过水轮机的水流量，达到调节的作用。如图1所示。其方框中为执行机构即被控对象。

1 遗传算法在水轮机调速系统的最优参数整定中的应用

1.1 PID最优参数的表示方法

水轮机调速系统参数的具体范围和精度要求都是由用户提出来的，然后对所要调节的参数进行二进制形式的编码，在二进制编码中，由于需要将二进制数转换为十进制数，因此存在量化误差，降低了寻优速度；实数值编码对原参数直接进行遗传操作，使寻优范围充满整个最优解可能存在的空间。本文中以实数值编码作为编码方式。

1.2 初始调速参数样本的选择

由于水轮机的调速系统的PID正定算法采用的是一种二进制算法，所以应该采用计算机随机产生的初始样本种群。此外，考虑到计算的复杂程度来规定种群的大小。

图1 微机型调速器框图

1.3 选择

一般来说，一个个体的适应值越高，它在种群中扩大的几率就越大，优良特性得到遗传的可能性也就越大。本文采用适应度比例方法与最优保留策略进行选择操作，种群中个体的选择概率为：

式中，f是个体适应度；f是种群总适应度；p是个体选择概率。

1.4 交叉/基因重组

基因重组又称交叉是将2个父个体的部分结构加以替代重组而生成新个体的操作，也称为交叉.采用中间重组方式，子个体按下式产生：子个体=×父个体1+（1－）×父个体2

式中，是一个比例因子，可由[O,1]上均匀分布的随机数产生。子代中每个变量的值均可按上面的表达式计算，但每个变量的值不同。

1.5 PID算法适配函数的确定

稳定性、准确性以及快速性是评价水轮机控制性能的主要三个指标。适配函数是遗传算法指导搜索的唯一信息，它的选取是算法的关键。根据控制性能的要求，参数选择的目标函数可按下列方法选取：

本文在最小目标函数方面的选择方面所采用的依据主要是误差绝对值的时间积分特性，主要目的是为了满足控制过程的动态特性。通过在目标函数中综合了控制输入的平方项，进一步实现了对输入能量过大或者超调的控制，针对超调采用的做法就是将其作为最优指标的一个项目。下面的时间积分方程是参数选取的最优指标：

上边目标函数是针对被控对象输入，输出及控制量进行考虑的，为了更符合水轮机调速系统的要求，还要对整个系统内部进行分析。

根据参考文献[2]有以下传递方块图，如图2所示。

图2 传递方块图

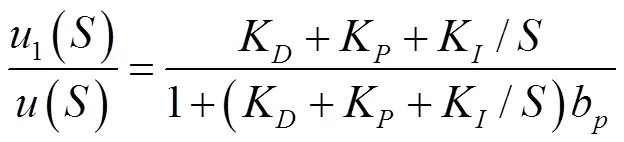
水轮机调速系统在小波动情况下，基于遗传算法的PID控制系统可以近似的假设成一个线性的系统，对于现行系统而言，其目标函数如下：

取理想水轮机模型系数对其仿真，其参数如下：

T=0.1s，T=3s，e=1.5s，e=0.1s，T=1.5s，

e=1.0s，e=0.5s，b=0.04s，T=8s。

设样本个数为30，交叉概率P=0.8，P=0.06；

参数K，K取值范围为[0，10]；

K取值范围[0,6]，取1=0.009，2=0.001，3=2.0，4=150。

图3 程序流程图

图4 目标函数J ′的优化过程

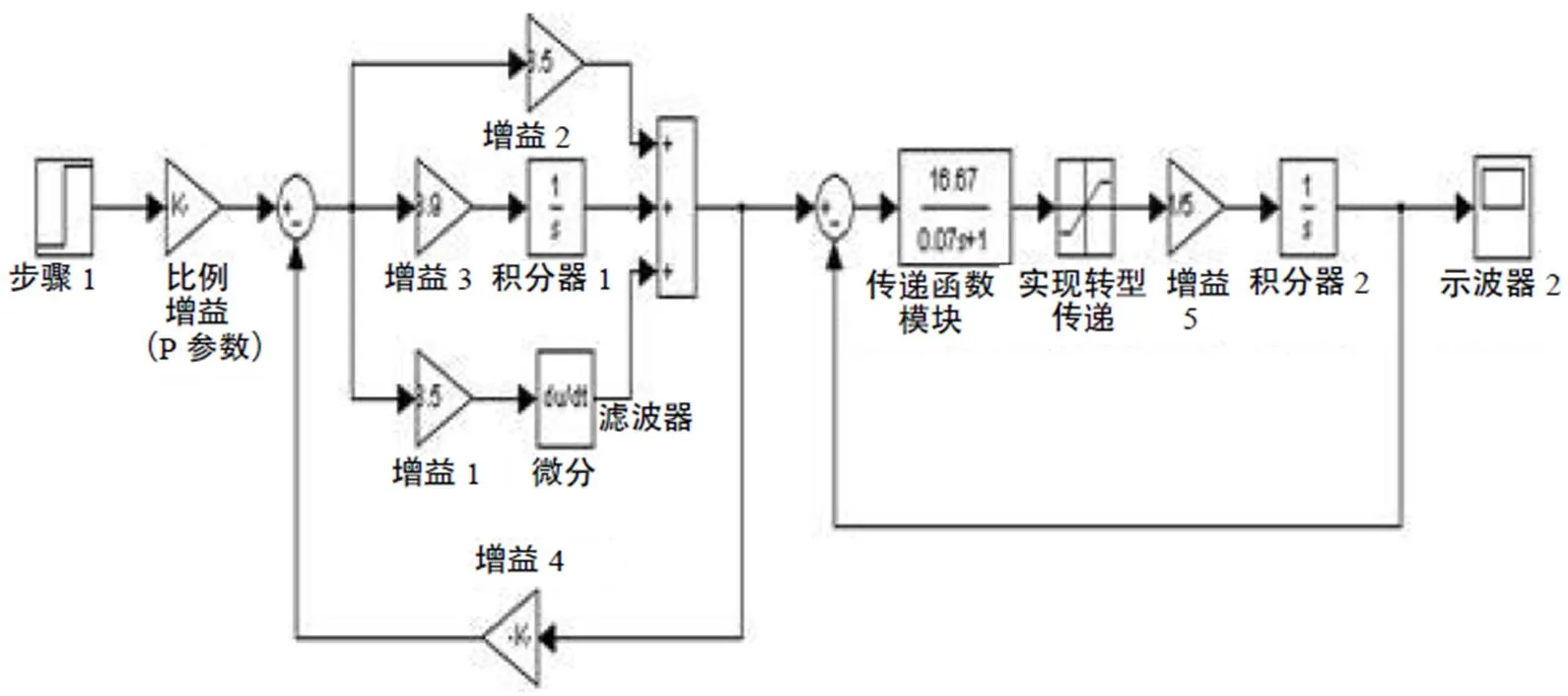
图5 SIMULINK仿真图

图6 仿真结果

SIMULINK仿真图用STEP代表转速、功率共同作用的偏差信号，通过仿真结果可以看出，遗传算法整定出的PID参数值使该控制系统无超调现象，并且调节时间在30s内，说明该整定方法能够满足调速器的要求，适合水轮机调速过程的控制。

2 结论

本文结合实际案例研究了遗传算法在水轮机调速系统PID正定控制过程中的应用，这种经过优化的计算方法的最优适配函数是根据系统的状态方程得来的。其整定结果通过MATLAB/SIMULIK仿真得到满意结果。该整定方法可对水轮机调速系统PID参数的设定起到一定的指导作用。

[1] 陈珩. 电力系统稳态分析[M]. 北京: 中国电力出版社, 1995.

[2] 魏守平. 现代水轮机调节技术[M]. 华中科技大学出版, 2001.

[3] 郭培源. 电力系统自动控制新技术[M]. 北京: 科学出版社. 2003.

[4] 王小平. 遗传算法理论应用与软件实现[M]. 西安:交通大学出版社. 2002.

[5] 李敏强. 遗传算法的基本理论与应用[M]. 北京:科学出版社, 2002.

[6] 刘金琨. 先进PID控制MATLAB仿真[M]. 北京：电子工业出版社, 2004.

Turbine Governor Based on Genetic Algorithm PID Parameter Tuning System

LONG Yonghui1, XIAO Kangle2

（1. SINOPEC. Southwest Petroleum Bureau. ChongQing Drilling Company, Chongqing 400042, China; 2. JiangSu Shahe Pumped-storage Power Generating Co.,Itd, Liyang213300, china）

Studing the genetic algorithm in the turbine governor control system PID definite course in this paper, the actual case study concluded that, PID regulator to adjust the current popular way. The original method of tuning the PID parameter of water turbine governor is mainly depended on experience. Through the use of genetic algorithms in combination with each other to control the parameters of PID, on which the turbine governor parameters Kp, Ki, KDhad varying degrees of optimization, and achieved good results.

water turbine governor; PID regulation; genetic algorihm

TK730.4+1

A

1000-3983(2014)02-0058-04

2013-04-20

龙永辉（1979-），男，2005年本科毕业于沈阳建筑大学，建筑机械专业；2008年研究生毕业于西南石油大学，石油机械专业。现主要从事油田钻井野外作业的现场技术工作，助理工程师。

审稿人：朴秀日