温度与应变率对Cu70Zn30孪晶变形的影响
2014-10-20周剑秋叶志雄
周剑秋,叶志雄,邱 奇,江 娥
武汉工程大学机电工程学院,湖北 武汉 430205
0 引 言
孪晶变形是塑性变形的主要方式,因为其独特的变形机理而被广泛的研究[1-4].共格孪晶界可以像晶界一样阻碍位错运动,从而提高材料的强度[5].研究发现,通过在多晶铜中引入纳米级的孪晶,材料的强度会达到1GPa[6].同时,当孪晶间距大小λ=15nm时,材料的强度会达到最大值,此后继续减小孪晶间距,材料的强度反而减小[7].低温和高应变率可以促进孪晶的形成,Christian与Mahajan[1]阐述了温度与应变率对粗晶面心立方晶格材料(FCC)的作用.众多实验证实,在常温准静态变形中适度的应变条件下,粗晶铜不会发生孪晶变形,然而在高应变率或者低温的条件下能够产生孪晶[8-13].上述文献表明,温度与应变率可以促进材料的孪晶变形,孪晶的存在对材料的性能有很大的影响.但是,目前关于温度与应变率对孪晶变形的影响人们了解的还是很少,中科院卢柯院士的研究表明[14],随着温度的降低与应变率的增加,孪晶的生长像一个“内嵌”的过程,不断的在未形成孪晶区域生成新的孪晶.笔者主要建立一个关于Cu70-Zn30的力学本构模型,模拟不同的温度与不同的应变率的情况下Cu70-Zn30的孪晶变形,并通过与实验结果相比较,预测孪晶变形过程中孪晶间距的演化过程.
1 理论模型
1.1 Cu70-Zn30的变形机理
滑移与孪生是材料塑性变形的主要变形机制,变形机理与材料的层错能大小有密切的关系.随着纯铜中锌的含量的增加,材料的层错能也逐渐减小,从纯铜的80mJ/m2减小到Cu70-Zn30的14mJ/m2[15].本实验研究的材料为 Cu70-Zn30,因为其层错能很小,容易形成层错,常温下会存在大量孪晶,孪晶变形成为其主要的变形机理.
1.2 Cu70-Zn30的流动应力
材料的流动应力主要归功于材料内部障碍对位错的阻碍作用,根据障碍作用范围的大小将流动应力分为短程应力与长程应力[16].短程应力可以通过热激活运动来克服,降低温度或者增加应变率可以导致短程应力增大.然而长程障碍主要包括晶界、孪晶界等其他微观结构,不随温度与应变率的改变而变化,长程应力主要与应变有关.因此,铜锌合金的流动应力可以描述为:
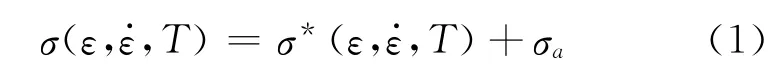
式(1)中σa是长程应力(非热应力),σ*为短程应力(热激活应力).由于热激活应力主要与温度、应变率有关,因此在本文中,热激活应力采用Johnson-Cook方程[17].
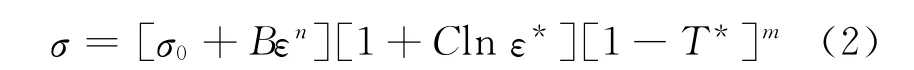
式(2)中,ε表示应变,T*=,T表示温度,Tm是材料的熔点温度,Tr为参考温度,本文取77K,ε*=表示应变,一般取0.001/s,σ0,B和n为材料常数,C与m分别表示应变率硬化指数与热软化指数.
长程应力采用幂次强化[16],主要与应变大小有关系,表述为

参照 OFFC Cu[16]以及粗晶铜[18]的拉伸实验数据分别取=380MPa,n1=0.4,引入施密特因子M,将剪切应力转化为

联合方程(2)与方程(4),材料的流动应力可以表示为

2 Cu70-Zn30的孪晶变形
塑性变形机理与材料的层错能大小有关联,Cu70-Zn30在常温下存在大量孪晶,其变形机理主要是孪晶变形.孪晶界阻碍位错的运动,从而提高材料的强度.为了能够很好的描述在不同条件下的孪晶变形,有必要去描述孪晶的结构原理图.孪晶片层与基体部分被晶面分开组成一个三维的孪晶晶粒模型,如图1所示,孪晶片层厚度用t表示,孪晶间距大小用λ表示.
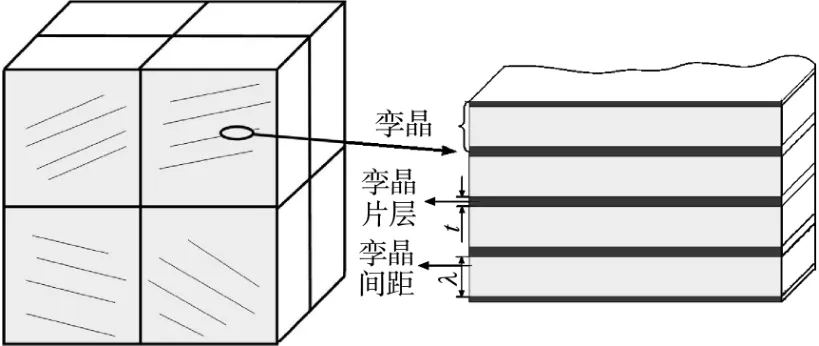
图1 理想状态下Cu70-Zn30的孪晶结构示意图Fig.1 Schematic framework of Cu70-Zn30alloy with twins
2.1 局部应力
根据泰勒位错硬化模型[19-20],对于FCC 材料,由于位错运动而引起的局部应力σ1为
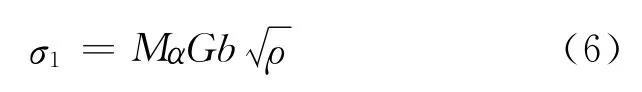
式(6)中,M=3.06表示泰勒常数,α表示经验常数,G是材料的弹性模量,b为柏氏矢量,ρ表示位错密度.在等位错分布的模型中,位错密度ρ与两个相邻障碍的距离ΔL 满足式子:ΔL≈ρ-1/2,在这里ΔL用孪晶间距λ代替,故

2.2 变形孪晶的应变硬化作用
孪晶界能阻碍位错的运动,因此晶体材料中的变形孪晶对其流动应力有着应变强化效应.随着塑性应变的增加,孪晶强化作用越明显,此外孪晶结构细化晶粒也提高了材料的应变硬化作用.晶体材料中的孪晶强化原理图如图2所示.

图2 孪晶强化原理示意图Fig.2 Schematic illustration of strain hardening about DTs
依照描述晶界滑移阻力的H-P关系,将孪晶界造成的位错滑移阻力的提高能力表达为

式(8)中,KT为孪晶变形时的 H-P斜率.联合式(7)与式(8)可以得到材料在孪晶变形时总的流动应力关系式为
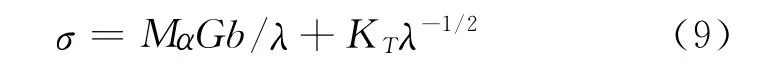
因此,式(5)与式(9)对等会得到孪晶间距λ与温度、应变率的关系式为
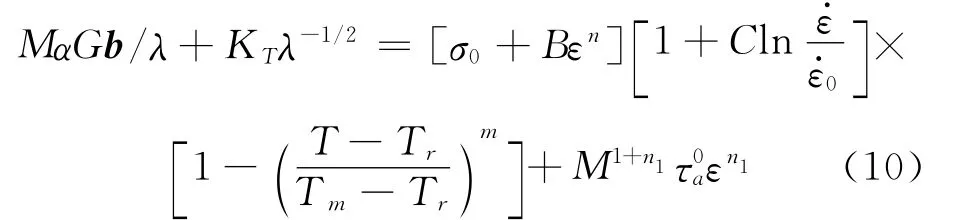
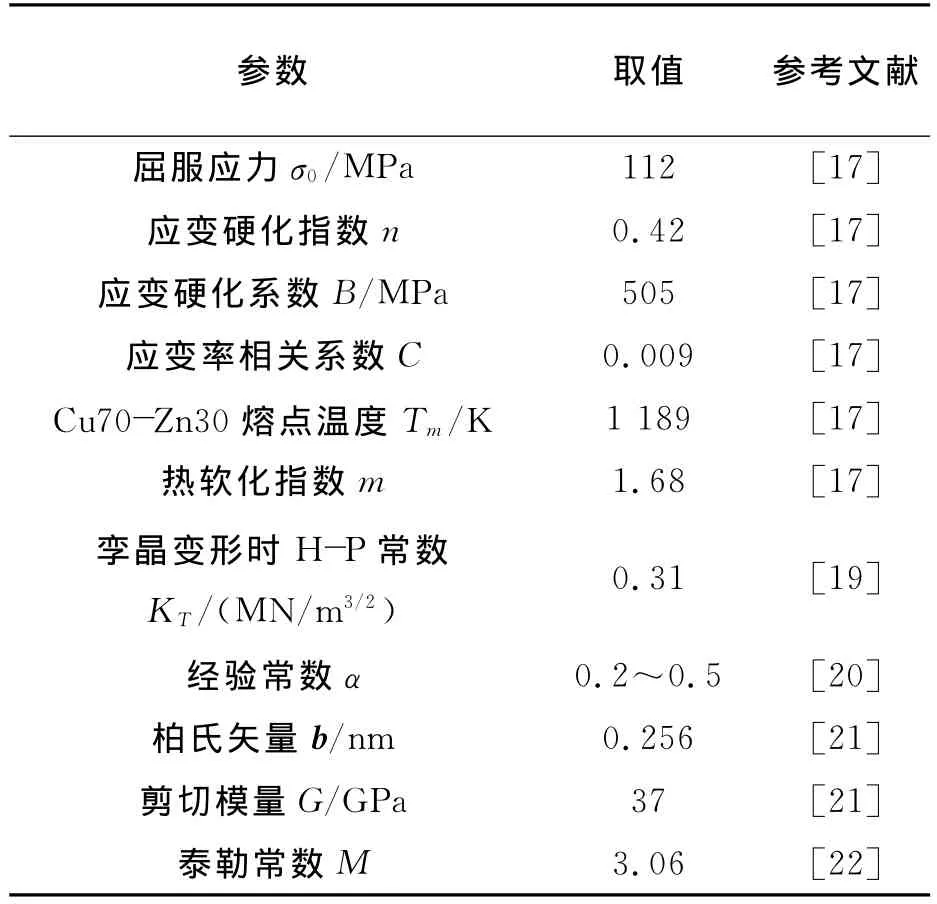
表1 方程(10)计算所需的参数Table 1 The parameters used in calculation in equation(10)
3 结果与讨论
3.1 结果与实验对比
为了验证式子(10)的合理性,将Cu70-Zn30的实验数据与数值模拟的结果进行比较,计算所需的参数如表1所示,实验数据来自于Xiao G H和Tao N R[14]等人的研究论文,首先采用氩气气氛炉对Cu70-Zn30进行退火,退火温度为700℃,退火时间为1h,获得了平均晶粒尺寸为110μm的Cu70-Zn30粗晶体结构,然后在液氮温度下对材料进行动态塑性变形(LNT-DPD)处理,发现Cu70-Zn30晶体内部有大量的纳米孪晶,并且随着应变的增加,孪晶片层厚度与孪晶间距不断减小.本文数值模拟了孪晶间距在液氮温度77K,应变率为1 000/s的变化曲线,如图3所示.
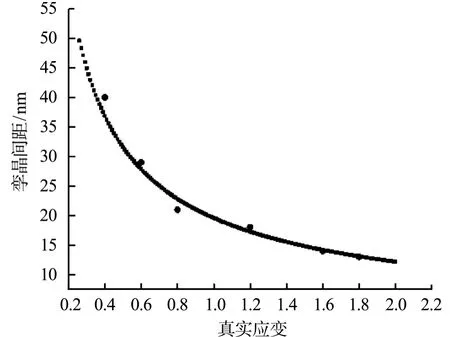
图3 Cu70-Zn30在温度为77K,应变率为1 000/s下孪晶间距-应变曲线与实验数据对比图Fig.3 Comparison between the calculated and experimental TB spacing-strain curve under dynamic plastic deformation at a liquid nitrogen temperature
从图3中可以看出,Cu70-Zn30在温度为77K,应变率为1 000/s下孪晶间距-应变曲线与实验数据能够很好的吻合.
3.2 孪晶片层厚度的演化过程
根据文献[23],孪晶间距与孪晶片层厚度的关系为

式(11)中t表示孪晶片层的平均厚度,f为孪晶的体积分数.
在塑性变形过程中,位错被孪晶界所阻碍,随着应变的增加,位错在孪晶界堆积形成应力集中.应力集中的程度大小与位错堆积的数量有关.如图4所示,对比实验数据[14],发现温度降低与应变率的增大均能导致孪晶片层厚度的减小,使得孪晶内部可塞积的位错数量减小,这就需要更高的驱动应力才能使位错穿过孪晶界,因此更小的孪晶间距与孪晶片层厚度可以增强材料的流动应力.

图4 Cu70-Zn30在应变率为1 000/s,不同的温度条件下孪晶片层厚度-应变曲线与实验数据对比图Fig.4 Comparison between the calculated and experimental Twin layer thickness-strain curve under dynamic plastic deformation at a liquid nitrogen temperature
3.3 温度对孪晶变形的影响
根据文献[24],在塑性变形过程中,需要考虑由于材料的变形而导致的绝热温升ΔT=σdε,其中,β=0.9(假设塑性变形中所做的功90%都转为热量),ρs=8.52g/cm2表示Cu70-Zn30的密度,为比热容(385J/kg·K).图5与图6分别表示铜锌合金在应变率为0.001/s和1 000/s,不同的温度的条件下的孪晶间距随应变的变化曲线.在温度范围为77K<T<1 096K,孪晶间距λ随着温度的降低而减小,温度的变化对孪晶变形的影响很大.主要是因为在低温的条件下,位错的运动受到抑制,而孪生应力与温度无关,因此低温的状态下,孪晶变形成为其主要的变形机理.塑性应变导致孪晶数量增多,材料内部的孪生区域也增大,从而引起孪晶间距的减小.前期生成的孪晶由于剧烈的塑性变形发生破碎,孪晶片层厚度减小.随着应变的继续进行,孪晶区域增加,未发生孪晶的区域减小,为后续孪晶的形成与生长所提供的空间也逐渐减小,故导致孪晶片层厚度与孪晶间距均减小.
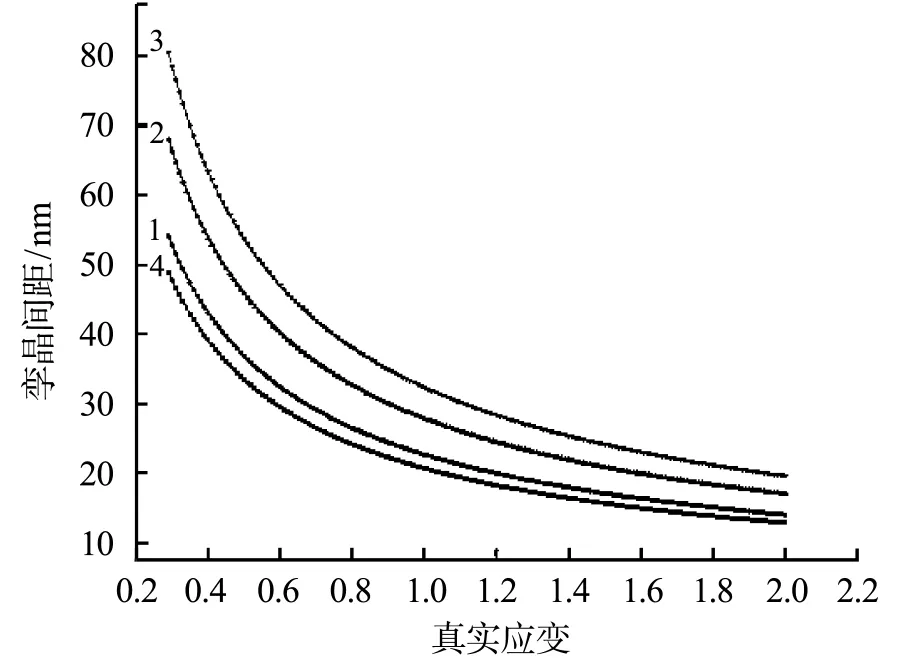
图5 Cu70-Zn30在应变率为0.001/s,不同的温度下孪晶间距变化的模拟结果Fig.5 The predictions for Cu70-Zn30at 0.001/s strain rate and indicated temperature
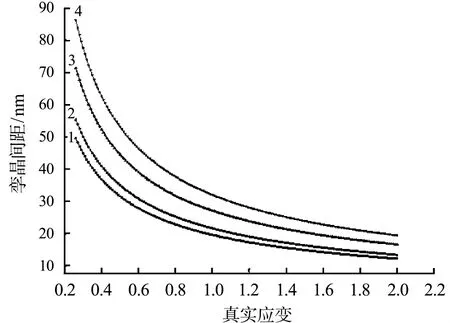
图6 Cu70-Zn30在应变率为1 000/s,不同的温度下孪晶间距变化的模拟结果Fig.6 The predictions for Cu70-Zn30at 1 000/s strain rate and indicated temperature
3.4 应变率对孪晶变形的影响
图7、图8分别表示铜锌合金在温度为77K和496K,不同的应变率的条件下的孪晶间距随应变的变化曲线,孪晶间距随着应变率的增大而减小,但是应变率的作用并不明显.图9中,三种不同条件下孪晶间距随应变变化曲线,其中在温度T=77K,ε·=0.001/s时,孪晶间距最小.对比图7、图8和图9发现,孪晶变形对温度要敏感的多.主要原因是应变率主要影响孪晶的形核与孪晶生长的时间.孪晶形核需要较高的应力集中,应变率越大,应力集中时间越短,形核速度越快,孪晶生长的时间越短,从而导致孪晶片层厚度减小,另外一方面,应变率越高,应变速度越快,孪晶的数量也随着应变增加,所以孪晶间距也减小.

图7 铜锌合金在温度为77K,不同的应变率的条件下的孪晶间距随应变的变化曲线Fig.7 TB spacing evolves with different strain rates at 77

图8 铜锌合金在温度为496K,不同的应变率的条件下的孪晶间距随应变的变化曲线Fig.8 TB spacing evolves with different strain rates at 496 1——1 000/s;2——1/s;3——0.001/s

图9 三种不同条件下孪晶间距随应变变化曲线Fig.9 TB spacing evolves with different strain rates at different temperatures
4 结 语
通过建立一个关于Cu70-Zn30的力学理论模型,模拟不同的温度与不同的应变率的情况下Cu70-Zn30的孪晶变形,并与实验结果相比较发现,低温与高应变率均能促进孪晶变形,孪晶间距与孪晶片层厚度随着温度的降低与应变率的升高而减小,但是材料的孪晶变形对温度的变化要更为敏感.
[1]CHRISTIAN J W,MAHAJAN S.Deformation twinning[J].Progress in Materials Science,1995,39(1):1-157.
[2]ZHU L,RUAN H,LI X,et al.Modeling grain size dependent optimal twin spacing for achieving ultimate high strength and related high ductility in nanotwinned metals[J].Acta Materialia,2011,59(14):5544-5557.
[3]KOCHMANN D M,LE K C.A continuum model for initiation and evolution of deformation twinning[J].Journal of the Mechanics and Physics of Solids,2009,57(6):987-1002.
[4]STEBNER A P,VOGEL S C,NOEBE R D,et al.Micromechanical quantification of elastic,twinning,and slip strain partitioning exhibited by polycrystalline,monoclinic nickel-titanium during large uniaxial deformations measured via in-situ neutron diffraction[J].Journal of the Mechanics and Physics of Solids,2013,61(11):2302-2330.
[5]MEYERS M A,VOHRINGER O,LUBARDA V A.The onset of twinning in metals:a constitutive description[J].Acta Materialia,2001,49(19):4025-4039.
[6]SHEN Y F,LU L,LU Q H,et al.Tensile properties of copper with nano-scale twins[J].Scripta Materialia,2005,52(10):989-994.
[7]SCHIOTZ J,JACOBSEN K W.A maximum in the strength of nanocrystalline copper[J].Science,2003,301(5638):1357-1359.
[8]JOHARI O,THOMAS G.Substructures in explosively deformed Cu and Cu-Al alloys[J].Acta Metallurgica,1964,12(10):1153-1159.
[9]CRIMP M A,SMITH B C,MIKKOLA D E.Sub-structure development in shock-loaded Cu-8.7Ge and Copper:the role of temperature,grain size and stacking fault energy[J].Materials Science and Engineering,1987(96):27-40.
[10]GRAY III G T,HUANG J C.Influence of repeated shock loading on the substructure evolution of 99.99wt.%aluminum[J].Materials Science and Engineering:A,1991,145(1):21-35.
[11]MURR L E,ESQUIVEL E V.Observations of common microstructural issues associated with dynamic deformation phenomena:Twins,microbands,grain size effects,shear bands,and dynamic recrystallization[J].Journal of Materials Science,2004,39(4):1153-1168.
[12]BLEWITT T H,COLTMAN R R,JAMISON R E,et al.Radiation hardening of copper single crystals[J].Journal of Nuclear Materials,1960,2(4):277-298.
[13]WANG Y,JIAO T,MA E.Dynamic processes for nanostructure development in Cu after severe cryogenic rolling deformation[J].Materials Transactions,2003,44(10):1926-1934.
[14]XIAO G H,TAO N R,LU K.Effects of strain,strain rate and temperature on deformation twinning in a Cu-Zn alloy[J].Scripta Materialia,2008,59(9):975-978.
[15]梁晓光,伞星源,杨鹏,等.Cu及Cu-Zn合金压缩行为机理的研究[J].昆明理工大学学报:自然科学版,2011,36(4):23-28.LIANG Xiao-guang, SAN Xing-yuan,YANG Peng,et al.Study on mechanism of compression behavior of Cu and Cu-Zn alloys[J].Journal of Kunming University of Science and Technology,2011,36(4):23-28.(in Chinese)
[16]NEMAT-Nasser S,LI Y.Flow stress of fcc polycrystals with application to OFHC Cu[J].Acta Materialia,1998,46(2):565-577.
[17]JOHNSON G R,COOK W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperatures[C]//Proceedings of the 7th International Symposium on Ballistics.Netherlands,1983:541-547.
[18]XIAO G H,TAO N R,Lu K.Strength-ductility combination of nanostructured Cu-Zn alloy with nanotwin bundles[J].Scripta Materialia,2011,65(2):119-122.
[19]BAHMANPOUR H,YOUSSEF K M,HORKY J,et al.Deformation twins and related softening behavior in nanocrystalline Cu-30%Zn alloy[J].Acta Materialia,2012,60(8):3340-3349.
[20]ZHANG S,ZHOU J,WANG L,et al.The effect of the angle between loading axis and twin boundary on the mechanical behaviors of nanotwinned materials[J].Materials & Design,2013(45):292-299.
[21]HAGHSHENAS M,KLASSEN R J.Indentation-based assessment of the dependence of geometrically necessary dislocations upon depth and strain rate in FCC materials[J].Materials Science and Engineering:A,2013(586):223-230.
[22]FISK M,ION J C,LINDGREN L E.Flow stress modelfor IN718accounting for evolution of strengthening precipitates during thermal treatment[J].Computational Materials Science,2014(82):531-539.
[23]KARAMAN I,SEHITOGLU H,BEAUDOIN A J,et al.Modeling the deformation behavior of Hadfield steel single and polycrystals due to twinning and slip[J].Acta Materialia,2000,48(9):2031-2047.
[24]MISHRA A,KAD B K,GREGORI F,et al.Microstructural evolution in copper subjected to severe plastic deformation:Experiments and analysis[J].Acta Materialia,2007,55(1):13-28.
