Ka频段设备自动校相模型优化

高 山，刘桂生，李天宝，何嘉靖，贵 宇

(太原卫星发射中心，山西太原 030027)

0 引言

Ka频段设备采用双通道单脉冲自跟踪体制，天线接收的信号经馈源分为和、差信号后，经不同接收信道变频、滤波处理后，送入基带解调方位、俯仰误差电压［1－3〛。因此设备中和、差信号由于传输通道不同而引入的相位差主要来自以下部分:①馈源之后因传输波导长度不同产生的相位差;② 场放、2级下变频器及连接线缆差异产生的相位差。该设备采用自动校相方法来消除上述相位差，达到调整自跟踪性能的目的［4－6］。而在实际工作中，由于自跟踪零点不准确时常出现自动校相检查失败的情况。本文通过分析自动校相模型，计算得到了自跟踪零点不准确引入的误差，并提出了新的数据处理方法，进一步增强了自动校相模型的适用性。

1 自动校相模型分析

在自动校相模型中，角误差解调是以和信号为基准的［7］。假设和、差信号分别为:

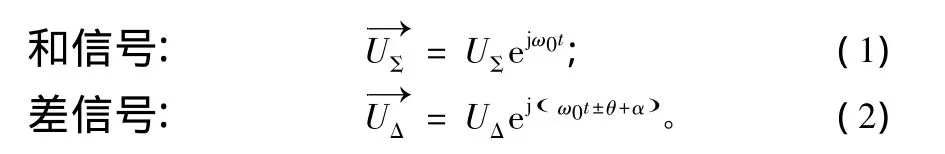
式中，ω0为载波角频率;UΣ、UΔ分别为和、差信号幅度;θ为天线未对准目标而引入的相位差(对于左旋信号取正号，对于右旋信号取负号);α为和差通道差异而引入的相位差，也就是自动校相中需要校准的通道移相值［8－12］。

本文将以左旋信号为例进行分析，对于右旋信号同理可得。

设备进行角误差解调时，实际上是求解下式:

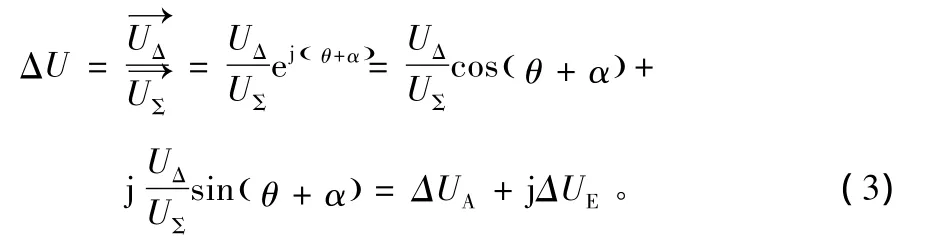
另外，理论上方位误差电压与俯仰误差电压是严格正交的，但由于装配工艺等原因，实际中两者不可能严格正交，即式(3)应表示为:

式中，αA为方位移相值;αE为俯仰移相值。

1.1 模型假设

假设1:理想情况下，和差通道无相位差，单向拉偏天线时误差电压为单向固定值。

在理想情况下(即和差通道无相位差，此时α=0，定向灵敏度为2400 mV/mil)，天线对塔，此时θ=0°，UΔ=0 V，计算得 ΔUA=ΔUE=0 V;天线方为正向拉偏1 mil，此时 θ=180°，UΔ= －2.4 V，计算得ΔUA= －2.4 V，ΔUE=0 V，如图1所示。其余3个方向单向拉偏时，方位俯仰误差电压以此类推。

假设2:实际情况下，和差通道存在恒定相位差，单向拉偏天线时误差电压为固定值。在实际情况下(即和差通道存在固定相位差，此时α为非零固定值，定向灵敏度为实际固定值)，天线对塔，此时θ=0°，UΔ=0 V，计算得 ΔUA=ΔUE=0 V;天线方位正向拉偏 1 mil，此时 θ=180°，UΔ为固定值，ΔUA、ΔUE均为固定值，如图2所示。其中，UΔ为总误差电压，ΔUA为其在横轴上的投影即方位误差电压，ΔUE为其在纵轴上的投影即俯仰误差电压。其余3个方向单向拉偏时，方位俯仰误差电压以此类推。显然，假设1、假设2是合理的。

自动校相模型是以上述2种情况为基础，建立模型实现自跟踪参数解调计算。

图1 理想误差电压

图2 实际误差电压

1.2 模型的建立

1.2.1 参数计算模块

自动校相模型中，需要计算的自跟踪参数包括方位移相值、俯仰移相值、方位增益和俯仰增益4个参数。

自动校相模型中，方位移相值和方位增益采用以下方法计算。当天线方位正向拉偏时，基带以步进0.5°，范围0 ～360°设置 αA(设置 αE=αA+90°)，分别计算式(4)结果，获得方位俯仰误差电压与αA的对应关系曲线，再对曲线进行拟合处理，寻找俯仰误差电压为0，方位误差电压负向最大点，反算此点的αA值，即为方位移相值。

同时，方位增益PA可以通道计算实际误差电压US和理论误差电压UL的功率差得到，即

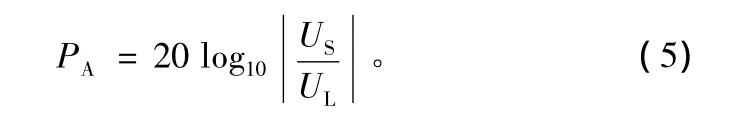
自动校相模型中，俯仰移相值和俯仰增益采用以下方法计算。当天线俯仰正向拉偏时，基带以步进0.5°，范围0 ～360°设置αE(设置αA=αE－90°)，分别计算式(4)结果，获得方位俯仰误差电压与αE的对应关系曲线，再对曲线进行拟合处理，寻找方位误差电压为0，俯仰误差电压负向最大点，反算此点的αE值，即为俯仰移相值。

同时，俯仰增益PE可以通道计算实际误差电压US和理论误差电压UL的功率差得到，即

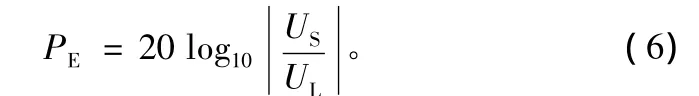
自动校相模型将天线4个方向单向拉偏时分别计算得到的4组自跟踪参数进行算术平均作为最终的自跟踪参数保存并下发。

1.2.2 性能检查模块

自动校相模型在参数计算结束后，天伺馈分系统进行自跟踪性能检查，主要包括:检查方位交叉耦合系数、方位定向灵敏度、俯仰交叉耦合系数和俯仰定向灵敏度。

在性能检查模块中，程序控制天线分别在方位、俯仰4向单向拉偏1 mil，记录方位俯仰误差电压，计算单向交叉耦合系数和定向灵敏度，并将判定结果上报监控。

1.3 模型的边界条件

在自动校相模型中，方位移相值和俯仰移相值范围均为360°，故当自动校相解算自跟踪参数时，需考虑0°和360°的边界条件，即当2次方位拉偏时，解算得到的方位移相值相差大于180°时，需要进行如下边界条件处理。

假设方位正向拉偏解算方位移相值为αA1，方位负向拉偏解算方位移相值为αA2，则最终方位移相值为:

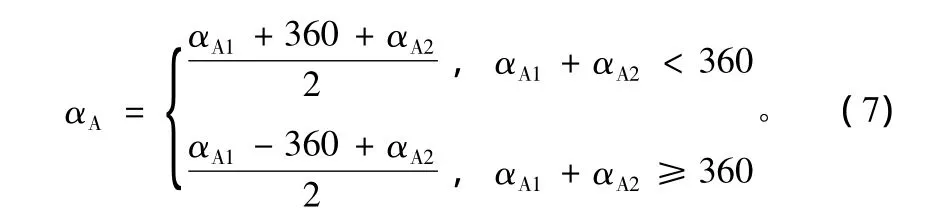
对于俯仰移相值的边界条件处理方法相同。

2 数据处理方法的优化

2.1 问题原因分析

通过对自动校相模型的分析，结合设备特点，对实际工作中出现的由于自跟踪零点不准确导致自动校相检查失败情况进行原因分析如下。

在自动校相模型中，默认了自动校相时需要找准自跟踪零点，这样在整个自动校相检查过程中，误差电压的变化才能正确反映天线拉偏动作，自动校相检查解算自跟踪参数才正确。

当自跟踪零点不准确时，自动校相检查过程中天线4个方向单向拉偏时，其实际误差电压如图3所示。

图3 天线单向拉偏误差电压

图3中，O为实际自跟踪零点;O'为自动校相检查中装填的自跟踪零点;图3(a)为按照自动校相检查流程相对于装填自跟踪零点O'产生的误差电压;图3(b)为自动校相实际解算时采用的误差电压。在装填自跟踪零点不准确情况下解调方位俯仰误差电压，相当于存在一个常值(即天线处于O'时产生的角误差电压值)，此时自动校相检查采用的角误差电压为:

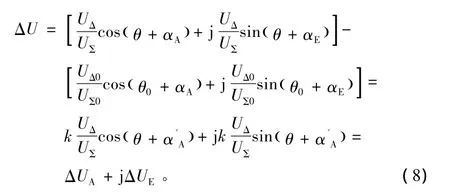
式中，为方便描述，式(8)中变量定义如下:

将式(8)与式(1)相比，当自跟踪零点不准确引入的测量误差不可忽略时，自动校相检查解算的方位移相值和俯仰移相值相当于增加了相位差(θ－θ')，方位增益和俯仰增益相当于变化了k倍。

而当自动校相使用的自跟踪零点偏差达到半功率波束宽度时，自动校相检查将无法解算方位移相值或俯仰移相值，自动校相检查中止。

该设备自动校相精度要求为5°，反算自跟踪零点不准确度最大为0.005°，而在实际工作中，Ka频段信号受环境影响，电零点漂移可达0.05°/24 h。在这种条件下，当前自动校相模型不利于设备自跟踪性能的调整，同时也限制了设备的机动能力。

2.2 数据处理方法优化建议

根据上述分析，在自动校相检查中若以相对装填自跟踪零点O'产生的误差电压解算自跟踪参数，解算结果即实际情况相符。故建议在当前自动校相模型作优化如下:① 在天线对塔后，记录天线位于装填自跟踪零点时的误差电压;②在天线单向拉偏后，记录当前误差电压;③ 如图4(c)所示，利用前两步结果计算相对状态自跟踪零点误差电压;④以第3步结果计算自跟踪参数;⑤ 对4方向结果取算术平均值。

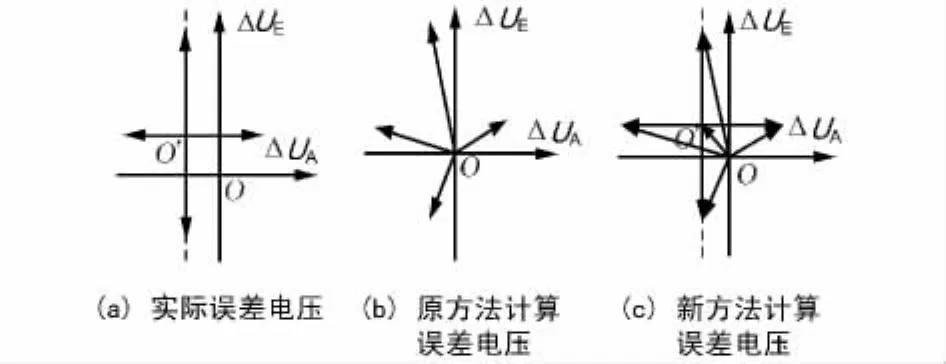
图4 向量法获取误差电压

需要说明的是，图4(a)为按照自动校相检查流程相对于装填自跟踪零点 O'产生的误差电压，图4(b)为现有自动校相检查解算自跟踪参数采用的误差电压，图4(c)为优化后自动校相检查解算自跟踪参数采用的误差电压。

3 结束语

针对设备自跟踪零点不准确引起的自动校相失败情况，对自动校相模型进行了分析，并对模型实现时的数据处理方法提出了优化建议。优化后的自动校相功能弱化了标校环境对设备自跟踪性能调整造成的影响，增强了对标校环境的适应性，提高了设备的机动参试能力。

在后续的模型改进中，还需要对下述情况进行深入分析，总结经验，从而为进一步优化完善自动校相模型提出合理化建议:①继续观察设备误差电压的特点规律，优化误差电压的选择使用方法;② 继续积累标校环境对误差电压和自动校相结果影响的经验，并以此对模型进行进一步完善，提高自动校相对标校环境的适应性;③从判定条件智能化方向继续探讨自动校相模型的优化建议，增强自动校相检查的科学性、合理性和智能性。 ■

［1］周志敏，李企舜.现代航天测控原理［M］.长沙:国防科技大学出版社，1998.

［2］黄学德.导弹测控系统［M］.北京:国防工业出版社，2000.

［3］赵业福.无线电跟踪测量［M］.北京:国防工业出版社，2003.

［4］袁 刚，江 涛.差模跟踪技术的应用［J］.现代雷达，2004(1):49－52.

［5］汪晓燕.单通道单脉冲角跟踪系统的研究［J］.电讯技术，2005(3):117－120.

［6］高京龙.单脉冲单通道跟踪体制精度分析方法［J］.无线电工程，2007，37(7):32 －34.

［7］李 靖，李 强，李 硕.单脉冲跟踪接收机相位自动校正的研究［J］.无线电工程，2008，38(5):56－58.

［8］王迎节，杨社年，聂 磊，等.天线跟踪和控制测量方法分析［J］.无线电通信技术，2011，37(4):31－33.

［9］李 勇，刘 洋.一种新型数字化中频调制解调器设计［J］.无线电工程，2012，42(5):27 －29，39.

［10］朱宏权，王俊峰.中频带宽对调频遥测解调性能的影响分析［J］.无线电工程，2013，43(6):17 －19.

［11］于开勇，李静芳，潘申富.载波相位误差对解调性能的影响分析［J］.无线电通信技术，2014，40(1):26－27，40.

［12］李 强.单通道数字跟踪接收机的设计［J］.无线电通信技术，2014，40(2):67 －69，89.