基于Matlab的IIR数字低通滤波器的设计方法

龚 涛

·（中国舰船研究设计中心，武汉 430064）

基于Matlab的IIR数字低通滤波器的设计方法

龚 涛

·（中国舰船研究设计中心，武汉 430064）

详细的阐述了IIR数字滤波器设计的一般步骤，首先根据给定的目标数字滤波器的性能指标，将其转换为模拟滤波器的指标参数，再根据巴特沃思（Butterworth）低通模拟滤波器的设计原理设计出相应技术指标下的模拟低通滤波器，最后采用双线性变换将设计出的模拟低通滤波器转换为数字滤波器，即得到了期望的IIR数字滤波器。针对实例，在Matlab环境下分别设计出了4阶、11阶、25阶的IIR数字滤波器，通过仿真验证了滤波器的速度与滤波效果之间不是完全的统一。最后，分析了双线性变换频率畸变现象，造成相同频率下离散后的幅值变小。通过频率预曲折方法对双线性变换进行相应的补偿。以25阶滤波器为例，仿真结果显示，在指定频率处实现了幅值在转换前后大小不变的效果。

数字滤波器，双线性变换，频率畸变，预曲折

0 引言

实现数字化是控制系统的重要发展方向，而数字信号处理已在通信、语音、图像、自动控制、雷达、军事、航空航天等领域广泛应用。数字信号处理方法通常涉及变换、滤波、频谱分析、编码解码等处理。数字滤波是重要环节，它能满足滤波器对幅度和相位特性的严格要求，能克服模拟滤波器所无法解决的电压和温度漂移以及噪声等问题。

数字滤波器从实现方法上有无限脉冲响应（IIR）滤波器和有限脉冲响应（FIR）滤波器之分，它们的设计一般都包括如下3个步骤：

(1)给出所需要的滤波器技术指标；

(2)设计离散系统传递函数H(z)使其逼近所需要的技术指标；

(3)实现传递函数H(z)设计系统。

FIR滤波器可以对给定的频率特性直接进行设计，而IIR滤波器目前最通用的方法是利用已经很成熟的模拟滤波器的设计方法来进行设计。而模拟滤波器的设计方法又有Butterworth、Chebyshev（I型、II型）、椭圆滤波器等不同的设计方法。模拟滤波器的设计已经有了一套相当成熟的方法，它不但有完整的设计公式，而且还有较为完整的图表供查询，因此，充分利用这些已有的资源将会给数字滤波器的设计带来很大的方便。

本文针对一个实例采用双线性z变换设计IIR低通滤波器，具体设计步骤如下：

(1)根据双线性变换s平面到z平面的映射关系，将给出的数字滤波器的性能指标转换为模拟滤波器的技术指标；

(2)依据转换后的技术指标设计巴特沃斯（Butterworth）模拟低通滤波器G(s)；

(3)再按一定规则将G(s)转换为H(z)，采用双线性Z变换。

设计流程图如下所示：

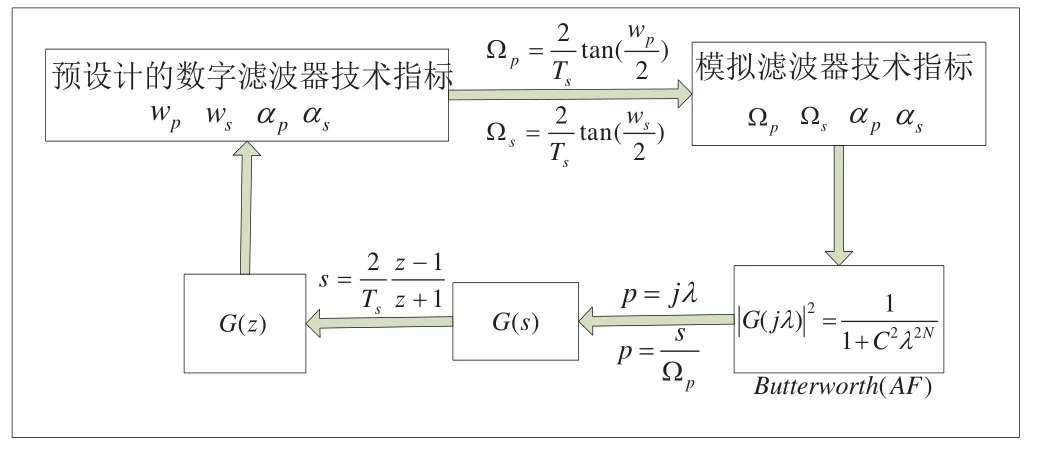
图1 双线性Z变换IIR数字低通滤波器设计流程图

1 滤波器设计过程

1.1 性能指标转换

数字滤波器设计首先要找到合适的映射关系，将其离散时间传递函数H(z)从z平面映射到连续时间传递函数的s复平面上，这种关系保证：

(1)s平面的整个jΩ轴只映射到z平面的单位圆上；

(2)若G(s)是稳定的，由G(s)映射得到的H(z)也应该是稳定的；

(3)这种映射是可逆的，既能由G(s)得到H(z)，也能由H(z)得到G(s)；

(4)如果G(j0)=1，那么H(ej0)也应等于1。满足以上4个条件的映射关系为：

此关系称为双线性z变换，由此关系不难求出：

用s平面和z平面中频率表示，由（1）中映射关系可以得到以下频率映射关系：

式（4）给出了s平面和z平面之间的频率映射关系。由此可知，s平面的虚轴对应z平面的单位圆。当Ω由0变至+∞时，z平面中ω相应的由0变至π；当Ω由0变至-∞时，z平面ω则相应的由0变至-π。这种映射正是利用了正切函数的非线性特点，把整个jΩ轴压缩到了单位圆的一周上。

这样，当给定了数字滤波器的技术指标：通带截止频率ωp、阻带截止频率ωs、峰值通带波纹αp、最小阻带衰减αs后，根据（4）式，有：

1.2 模拟低通滤波器设计

Butterworth低通滤波器的设计可按以下3个步骤来进行。

(1)将实际频率Ω归一化得到归一化的幅平方特性。

由此可以看出，在|G(jλ)|2中只有两个参数C和N，N是滤波器的阶次。

(2)依据由目标数字滤波器技术指标转换后得到的模拟滤波器技术指标，求出参数C和N。

由式（9）可得：

这样C和N便可求出。

3)确定G(s)

若令αp=3dB，则C=1，则Butterworth滤波器形式如下：

因为p=jλ，有

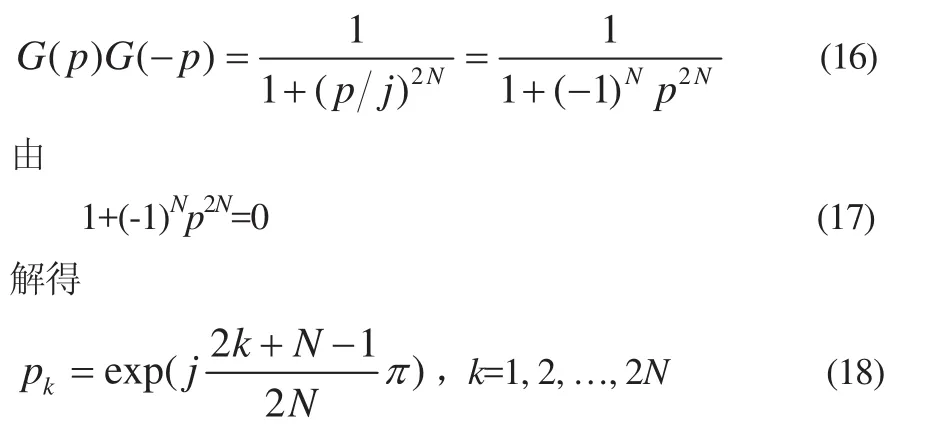
由上式解可以看出，2N个极点将均匀分布在s平面的半径为1的圆上，相距(π/Ν)rad。为了保证所设计的滤波器是稳定的，应将前N个极点，即位于s平面左半平面的N个极点赋予G(p)，即

这样，得到了归一化的转移函数G(p)。因为p=jλ=jΩ/Ωp=s/Ωp，所以，在求得G(p)后，用s/Ωp代替变量p，即得到实际需要的G(s)。

1.3 双线性变换

上述Butterworth低通模拟滤波器G(s)，即是由期望的数字滤波器技术指标转换后而求出的相应的模拟滤波器。利用双线性z变换，即可获得具备期望技术指标的IIR数字低通滤波器H(z)，即

1.4 畸变修正

由于双线性变换采用了正切函数的非线性特点，将s平面jΩ轴一一映射到z平面的单位圆周上，高度压缩必然导致频率映射的非线性，即出现畸变现象。

以一些具体的数据可以看出，s平面及z平面中出现的频率畸变如下表所示：

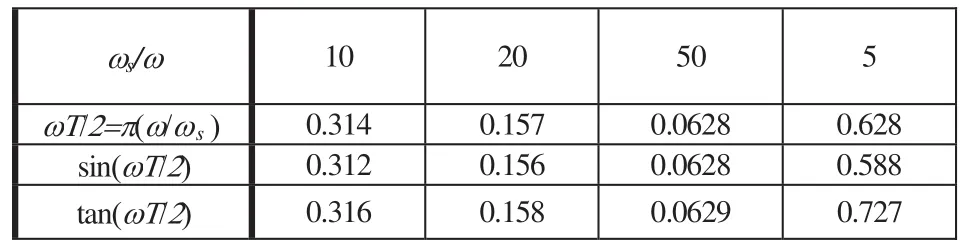
表1 具体数据举例

由上表数据可知，

图2 双线性变换出现的频率畸变

为了减小畸变的影响，就应修正双线性变换，以确保在某一频率处变换前后的幅值相同，即。具体步骤如下：

1)计算预修正频率ω∗

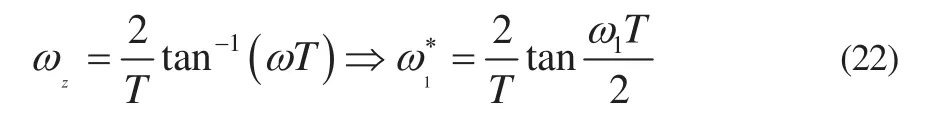
2)将D(s)修正为

3)采用频率预曲折的方法对双线性变换进行相应的补偿，修正后的双线性变换表达式如下：

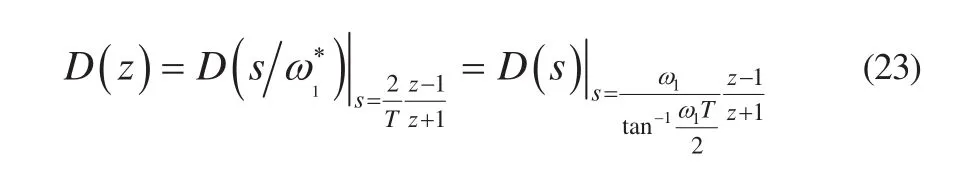
3 IIR数字滤波器设计实例

此节，针对具体实例进 IIR数字滤波器的设计。对一个含有2、3、5次谐波和高斯噪声的交流电流进行滤波，滤除3次及5次谐波，得到只含有基波和2次谐波的电流，采样频率是1kHz，具体参数如下表。

表2 含谐波、噪声电流具体参数

3.1 双线性变换设计IIR数字滤波器

详细程序设计：

运行程序，仿真波形如下所示：

图3 输入信号的时域波形与频谱

图4 fp=105Hz,fs=145Hz,αp=3dB,αs=12dB 技术指标下的4阶IIR数字滤波器滤波效果

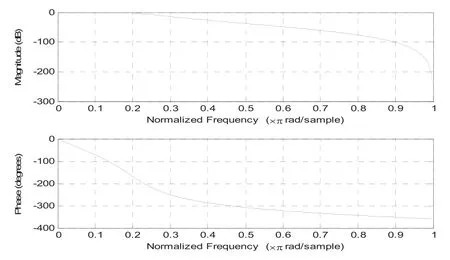
图5 fp=105Hz,fs=145Hz,αp=3dB,αs=12dB 技术指标下数字滤波器的幅频特性

在以上给定技术指标下，得到的4阶IIR数字滤波器已经将5次谐波完全滤除，3次谐波大大衰减，但是仍含有部分3次谐波。为了增强滤波效果，获得更加陡的幅频特性，缩短了fp与fs之间的过渡区域，并增大了阻带频率开始处的下降增益αs，由滤波器的设计过程可知，所获得滤波器阶数将会相应增大。技术指标修改如下：fp=110Hz,fs=135Hz,αp=3dB,αs=20dB获得11阶的IIR数字滤波器，滤波效果如下所示。

图6 11阶数字滤波器滤波效果

可以看出，信号中3次、5次谐波已经完全被消除，从其频谱图中可以看出，在通带0-100Hz以内，却出现了幅值比较低的连续频率信号。此时滤波器的幅频特性如下所示。由幅频特性可以看出，所设计的数字滤波器出现比较大的负的相位裕度，此滤波器如果加入实际系统将会造成系统的不稳定。

图7 11阶滤波器幅频特性

继续增大滤波器阶数，给定数字滤波器技术指标如下：fp=110Hz,fs=125Hz,αp=3dB,αs=30dB,得到25阶数字滤波器，其滤波效果及频谱特性如下图所示。可知，出现的杂频相对更加明显，幅频特性也出现更大的负的相位裕度。

图8 25阶数字滤波器滤波效果

图9 25阶滤波器幅频特性

由以上仿真可知，滤波器的阶数越高，滤波的幅频特性越陡，即滤波速度越快。但是却带来了更大的负的相位裕度，同时也引入了在通带0-100Hz内的其他杂频。可知，在滤波速度与效果上不是完全统一的。

3.2 频率预曲折修正双线性变换

由以上仿真结果可知，经过滤波后，虽已滤除了3次、5次谐波，但是由于双线性变换的频率畸变导致2次谐波幅值有些变小。此时，要保证基波及2次谐波处幅值在离散前后不发生变化，需要利用频率预曲折方法对双线性变换进行相应的补偿。指令如下：

[num1 den1]=C2DM(num,den,Ts,'prewarp',100);

即在频率100Hz处保证离散前后幅值大小不发生变化。

图10 修正后的25阶滤波器滤波效果

可知，经过频率预曲折方法修正后的双线性变换，在指定频率处的幅值大小与原信号2次谐波幅值大小保持不变。达到补偿的效果。

4 结论

本文详细的阐述了IIR数字滤波器设计的一般步骤，即首先根据给定的目标数字滤波器的技术指标，将其转换为模拟滤波器的技术指标，再根据巴特沃思（Butterworth）低通模拟滤波器的设计原理设计出相应技术指标下的模拟低通滤波器，最后采用双线性变换将设计出的模拟低通滤波器转换为数字滤波器，即得到了期望技术指标的IIR数字滤波器。

针对实例，设计出了4阶IIR数字滤波器，达到较为理想的滤波效果，3次、5次谐波已基本被滤除。通过改变技术指标，分别设计了11阶、25阶数字滤波器，通过仿真，验证了滤波器的速度与滤波效果之间不是完全的统一。阶数越高，滤波特性越陡峭，速度越快，但同时造成较大的负的相位裕度，也引入通带的其他杂频。

最后，分析了双线性变换频率畸变现象，在z平面上相映射的频率要小于其在s平面上所对应的频率，并且相同频率下z平面与s平面中所对应的幅值也不相同，造成相同频率下离散后的幅值变小。通过频率预曲折方法对双线性变换进行相应的补偿。以25阶滤波器为例，仿真结果显示，在指定频率处实现了幅值在转换前后大小不变的效果。

[1]丁美玉.数字信号处理.西安：西安电子科技大学出版社，2005

[2]S.K.Mitra.Digital Signal Processing–A Computer-Based Approach,Third Ed.,McGraw-Hill,2005

[3]郑南宁.数字信号处理.北京：清华大学出版社，2007

[4]张德丰.MATLAB数字信号处理与应用.北京：清华大学出版社，2010

[5]陈怀琛.数字信号处理教程.北京：电子工业出版社，2009

[6]葛哲学.精通MATLAB.北京：国防工业出版社，2008

Designing and Implementation of Lowpass IIR Digital Filter

GONG Tao
(China Ship Development and Design Center,Wuhan 430064,China)

This paper described the general steps of IIR digital filter design.Firstly,the given specifications of the digital filter were converted to those of the equivalent analog filter.Then,a low pass analog filter with the specifications was implemented according to the Butterworth low-pass analog filter designing method.Finally,the analog filter was converted to the correspondent digital filter by using bilinear transform so that the desired IIR low-pass digital filter was derived.For verification,in the MATLAB environment the 4-order,11-order and 25-order IIR low-pass digital filters were designed and verified by simulation.The results have shown that the speed and the filtering performance cannot be balanced.Finally,the frequency distortion phenomenon of the bilinear transform was analyzed and it is demonstrated that the amplitude in the same frequency will be small after discretization.Therefore,the Prewarping method can be used to compensate the bilinear transform appropriately.Simulations of a 25-order digital filter verify the validity of the compensation effect of the frequency prewarping.

digital filter,bilinear transform,frequency distortion,prewarping

U665.14

A

龚涛（1975-）， ，硕士，高级工程师，研究方向：电气工程。