模糊可变集合及其应用

陈守煜，薛志春，李 敏

（大连理工大学 水利工程学院 水资源与防洪研究所，辽宁 大连 116024）

0 引 言

1999年蔡文研究员在科学通报杂志上发表了题为 《可拓论及其应用》的综合性论文［1－2］。该文总结了1983年以来可拓学 （物元模型或物元分析）的代表性研究成果［3－5］。2000～2003年又相继在中国工程科学等杂志上发表了可拓学的工程应用与新进展等文章［6－8］。由此可拓学受到了科学与技术界相关研究人员的关注。

笔者在研究中发现，可拓学论著 ［1－6］给出的以 “距”与 “位值”概念为基础，实轴上点x的关联函数公式 （1）是错误的，不能在工程领域中应用，因为在工程上的误用，可能导致严重的后果。

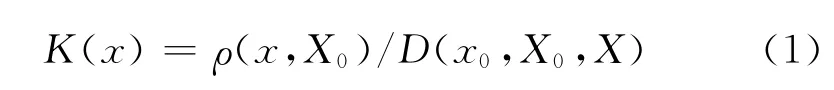
式中X0＝ ［a，b］，X＝ ［c，d］，X⊃X0，且无公共端点。

同时，文献 ［1－8］中建立给出的可拓学的基础概念：零界元素及关联函数，存在一定的问题。由于可拓学是一门以解决事物矛盾问题为研究对象，横跨哲学、数学与工程学的横断学科，这些问题的存在直接影响可拓学基础的科学性。

为了有助于工程模糊集理论与可拓学的发展，本文首先根据自然辩证法关于运动的矛盾性原理，分析文献 ［1－8］中可拓集合的零界概念与关联函数存在的问题，证明关联函数式 （1）是错误的。然后根据工程模糊集相对隶属函数有关概念与理论［9］，建立模糊可变集合的概念、定义，并给出应用实例。

1 文献 ［1－8］零界概念与关联函数存在的问题

文献 ［1］对零界元素的论述为：“零界元素描述了质变的临界点，零界元素既有性质˜A，又不具有性质˜A，如一只脚在门内，一只脚在门外的人，既属于门内的人的集合，又属于门外的人的集合”；并在数学上用关联函数K（u）＝0来描述零界元素u。文献 ［4］的论述为：“在导电的导体和不导电的绝缘体之间存在既导电、又不能导电的半导体；在酸性物体和碱性物体之间存在中性的盐；0℃的H2O处于既是液态又是固态的状态。显然，在自然界和社会生活中，存在大量这样的临界事物……。在可拓集合的框架里，承认了临界事物的存在，并用K（u）＝0来描述这些临界元素。”上述零 （临）界元素概念、关联函数的数学表达式K（u）＝0，无论在哲学或数学上都存在问题。

恩格斯在 《自然辩证法》一书中明确指出：“一切运动都存在于吸引和排斥的相互作用中。”［10］《自然辩证法原理》［11］一书中对此作了系统的阐述。就物质系统运动形式的内在矛盾及其相互转化而言，无论是自然界的物理运动、化学运动、宇宙的天体运动，还是生物界的生命运动，无一不反映出吸引和排斥的两极对立。如物理运动中的 “宏观热现象，本质上是大量分子或原子、电子等微观粒子不规则运动的外在表现。大量分子因分子引力而凝聚，因无规则运动相互排斥而扩散，两者相互作用的强弱不同，使物体形成不同温度下的不同热运动状态。例如，水在加热汽化时，分子的动能 （排斥）超过分子引力而自由扩散，排斥占优势，变成蒸汽；水在冷却结冰时，分子的动能较小，而吸引占优势，于是分子有序排列，结晶而成固态。各种宏观电磁现象，归根结底都是带正、负电荷的粒子之间的吸引和排斥相互作用构成的运动。正电荷和负电荷、磁北极和磁南极、导体和磁体之间，都显示出吸引和排斥的统一。”基于自然辩证法的 《哲理数学基础》［12］一书中对吸引与排斥作了详细地论述：“吸引和排斥是人类社会和自然界普遍存在的一对作用：吸引使事物相互接近和聚集；排斥使事物彼此分开和离散。它们相互制约、相互依存、相互补充，并在一定的条件下相互转化，因而是对称的，也就是对立统一的。由于吸引和排斥相互依存、相互补充而达到近似的平衡，乃有物体的有规则运动。……吸引和排斥的相互作用之关键性作用，不仅在宇宙、星系和恒星的演化中，在化学元素的起源和进化中，在太阳系和地球的演化中，在物质的化学进化中，表现得非常充分，而且在生命体的同化和异化、遗传和变异，以及新陈代谢和自我复制过程中也表现得非常充分。在自然系统中是如此，在社会系统中也不例外。”由以上论述可知，事物质变点的描述根据自然辩证法应是：事物u具有相当于吸引性质的程度（u）与具有相当于排斥性质的程度（u）达到动态平衡状态。其数学表达式为（u）＝（u），或（u）＝（u）－当时，事物u以为其主要性质，为次要性质，当时则相反。当事物从转化为（u），或从转化为即事物发生质变时，必通过质变点文献［1］用“一只脚在门内，一只脚在门外的人，既属于门内的人的集合，又属于门外的人的集合”来说明“零界元素既有性质，又不具有性质”，这不是现象的本质描述。因为一个人从“门内人”集合，转化为“门外人”的集合要有一个过程。当他跨向门槛，身体（可用体重或体积特征计）一半在门内，另一半在门外（不妨近似的认为：一只脚在门内，一只脚在门外），显然，此时他具有门内人、门外人集合的程度各占一半，即处于动态平衡状态。此种状态不是“既属于门内的人的集合，又属于门外的人的集合”，而是“该人具有门内人集合程度与门外人集合的程度相等”。因此，不是关联函数K（u）＝0，而应该是文献［4］以自然界与社会生活中存在临界事物，诸如0℃的水处于既是液态又是固态等状态，作为零（临）界与关联函数K（u）＝0的数学依据，这也不是事物矛盾运动变化：吸引与排斥的本质描述。

文献［1－6］建立给出实轴上点x的公式（1）来表述可拓集合中的关联函数，试图把“具有性质”的事物从定性描述扩展到“具有性质的程度”的定量描述。根据笔者的研究，关联函数式（1）是错误的，现证明如下。

证明可分为（1）递增系列，c＜a＜b＜d；（2）递减系列，c＞a＞b＞d两种不同的实际情况。下面首先给出递增系列c＜a＜b＜d的证明。

当x∉X0，按照文献［1－6］建立给出的“距”与“位值”有关概念的规定，参照图1箭头方向的递增情况，应有：

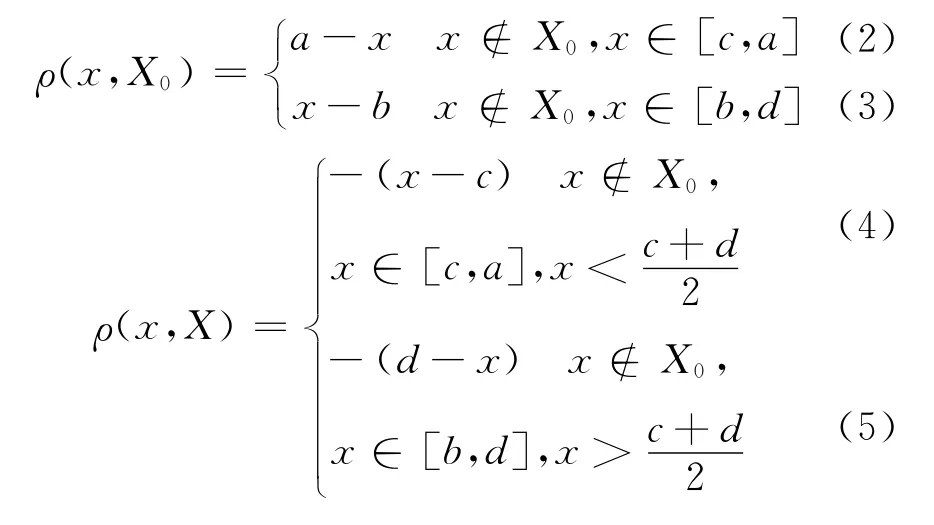
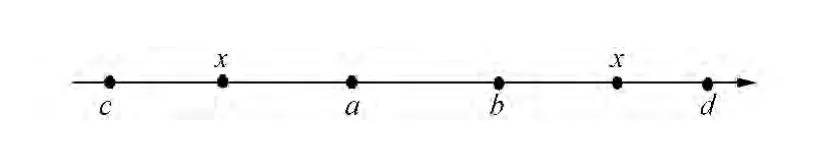
图1 可拓集合中“距”与“位置”变化示意图Fig．1 The changing schematic of“form”and“value”in the extension set

实轴上点x落入区间［c，a］或［b，d］是一个不相容事件，当x∉X0时，存在4种约束条件：式（1）可表为：

显然，上式只有当ρ（x，X）与ρ（x，X0）在相同的区间约束条件下，才是正确的。由式（2）、式（3）与式（4）、式（5）可见，关联函数式（1），只有在约束条件①、③下才有意义。即：

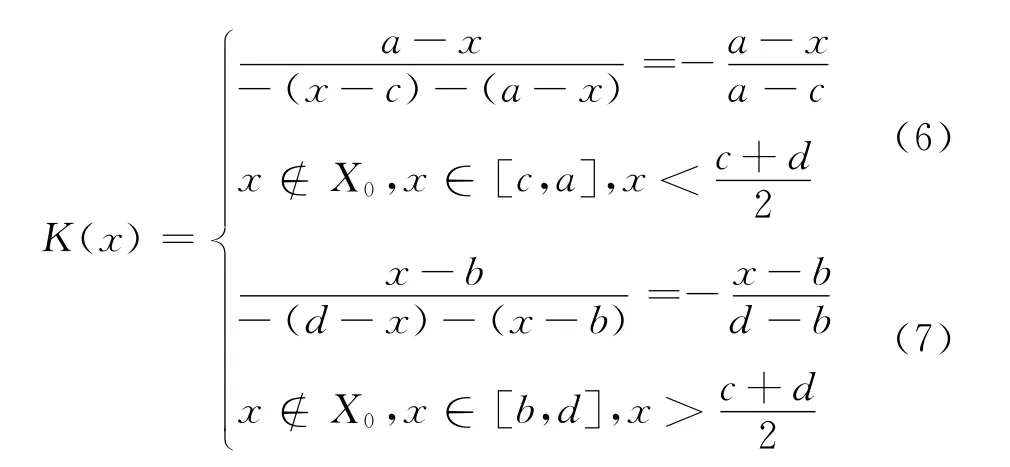
约束条件②、④关联函数式（1）有误。

当x∈X0，设M 为图1实轴上［a，b］区间上关联函数的最大点值。当x∈X0，且x∈［a，M］，即x点落在M 点的左侧时，建立区间［a，M］上的关联函数才有意义。此时要求满足则：

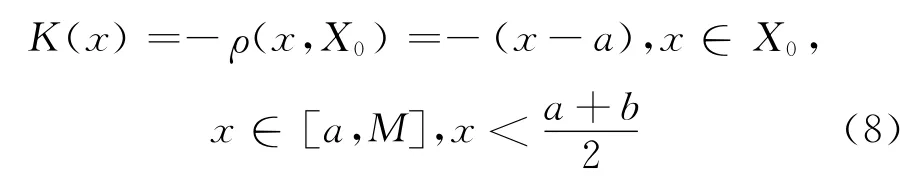
又当x∈X0，且x∈［M，b］时，有意义的是建立［M，b］区间上的关联函数。此时，要求满足约束条件则：

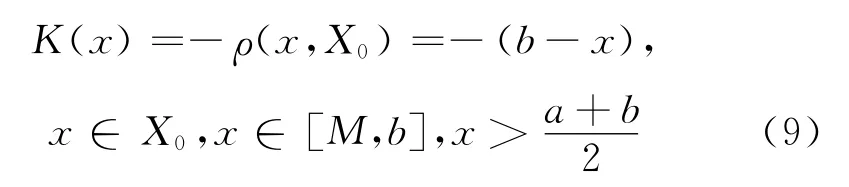
同样，当x∈X0实轴上点x落入［a，M］或［M，b］是不相容事件，当x∈X0又有4种情况：⑤x∈显然，当出现⑥、⑧关联函数式（1）有误。

应该指出，只有当点M 在区间［a，b］的中点时，约束条件⑤至⑧才能够全部满足，但事实上，在实际工程问题中，M 点不一定在［a，b］区间的中点。

在可拓学的一些论著［4－5］中，当x∈X0，对关联函数式（1）作了归一化处理，把ρ（x，X0）除以区间［a，b］的长度，即：

上式也有误，正确的应是：

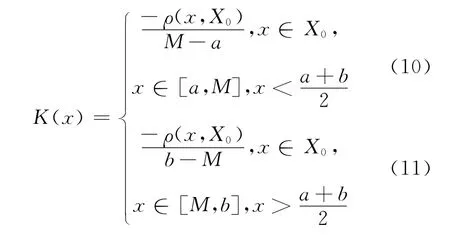
应该强调指出，当x∉X0时，点x落入区间［c，a］或［b，d］是一个不相容事件。当x∈X0时，点x落入区间［a，M］或［M，b］是又一个不相容事件。在实际工程领域中，将有点群xi很多次出现落入区间［c，a］或［b，d］以及［a，M］或［M，b］的约束条件①至⑧，当出现约束条件②、④、⑥与⑧，应用关联函数公式（1）就有误。因而总体来讲，只要有一个点x遇到 ②、④、⑥、⑧中的任何一种情况，就使得工程计算结果失去科学性，甚至导致最后成果有误。因此，可拓学论著［1－8］建立给出的以“距”与“位值”概念为基础的关联函数式（1）难以在实际工程领域中应用。

类似地，可以证明当为递减系列c＞a＞b＞d时，可拓学论著［1－6］中关联函数式（1）的错误，限于篇幅，证明从略。

2 以相对隶属函数为基础的模糊可变集合概念与原理

为了探讨研究解决上述可拓集合的零界元素与关联函数存在的问题，笔者以工程模糊集理论［9］为基础，建立以相对隶属函数为基础的模糊可变集合概念、理论与方法。

定义2．1 设U 为论域，u为U 中的任意元素，u∈U。（u）与（u）分别为事物u所具有的表征吸引性与排斥性程度的相对隶属函数［13－14］。令：

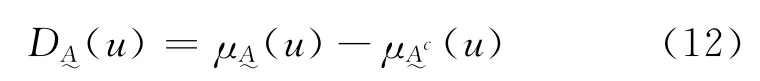
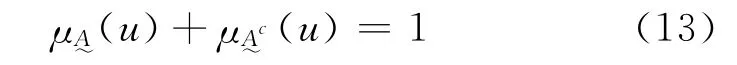
则D（u）是U到区间［－1，1］的一个映射，称为论域U关于元素u的相对差异度或相对差异函数，简称差异度或差异函数。

定义2．2 设U 为论域，u为U 中的任意元素，令：

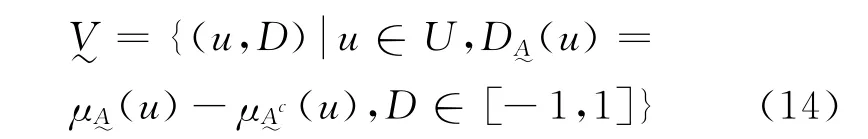
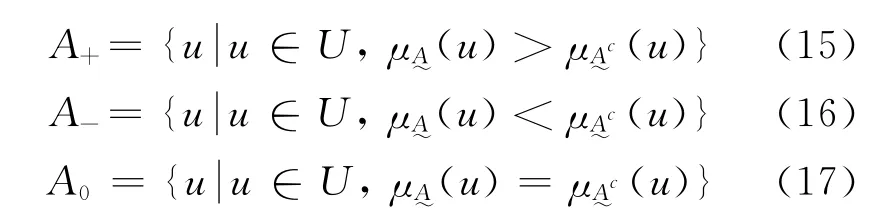
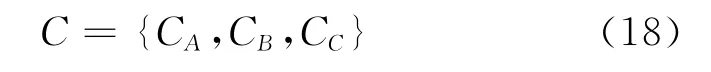
CA为模型可变集，CB为模型参数可变集，CC为除模型及其参数外，可变其他因素集。令：

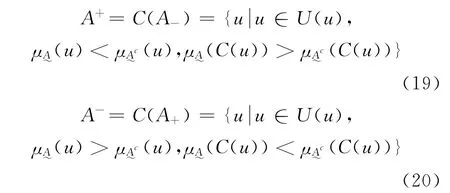
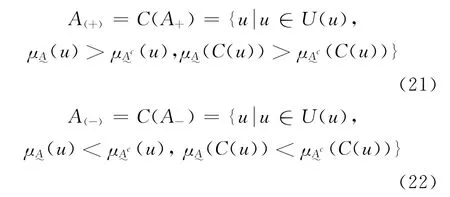
模糊可变集包括笔者在工程模糊集理论中提出的模糊优选模型［15］、模糊模式识别模型［16］、模糊聚类循环迭代模型［17］，以及模糊决策、识别与聚类的统一模型［18］等。模型的参数可变集包括模型的指标权重、指标标准值等重要模型参数。有关模型与模型参数的可变性，将在模糊水文学应用实例中给出相应的说明［19－21］。

3 相对隶属函数公式

设X0＝［a，b］为实轴上模糊可变集合的吸引（为主）域，即u（p）＞u（pc）区间，X＝［c，d］为包含X0的x的范围域或x的范围区间X0⊂X（图2）。

根据模糊可变集合定义可知［c，a］与［b，d］均为其排斥（为主）域，即u（p）＜u（pc）区间。设M为吸引（为主）域区间［a，b］中u（p）＝1的点值，在通常情况下M为区间［a，b］的中点值。设x为X区间内任意点的量值，则x落入M 点左侧时的相对隶属函数公式为：

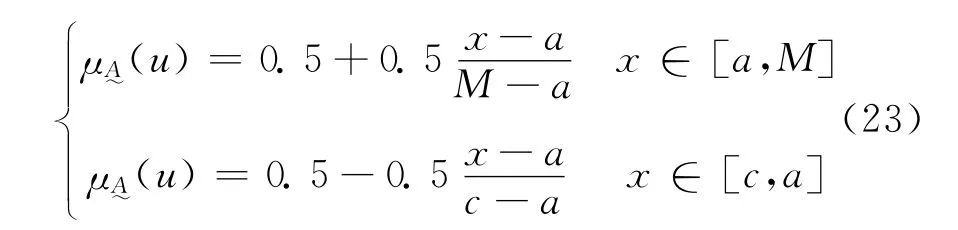
x落入M 点右侧时，其相对隶属函数公式为：

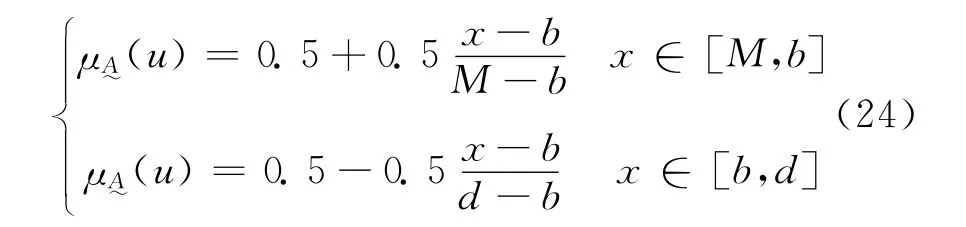
4 应用实例

为了比较模糊可变集合与可拓集合在应用中计算结果的科学性，引用文献［5］中列举的一个算例：已知某一人类化石数据

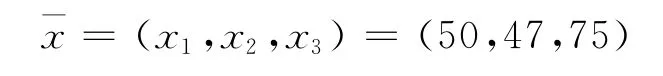
试应用模糊可变原理识别该化石属于人的程度。根据资料确定3项识别指标相关数据为：①颅盖高指数；②前囱角；③额角。已知有关数据为：

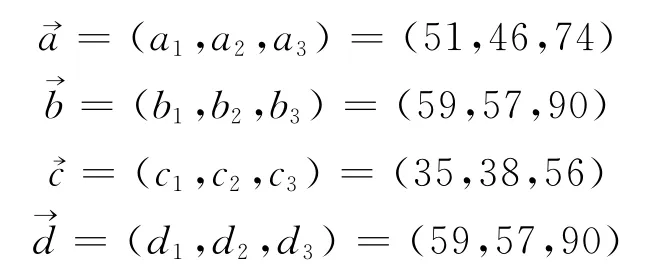
应用模糊可变原理计算如下。

应用笔者在文献［9］中提出的模糊优选可变模型：

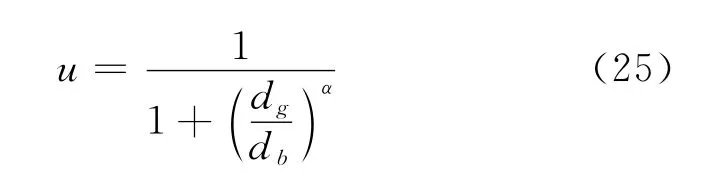
式中

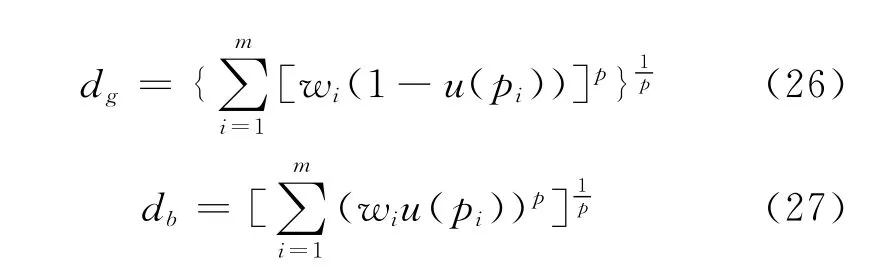
其中u为综合相对隶属度；α为模型优化准则参数，α＝1为最小一乘方准则，α＝2为最小二乘方准则；p为距离参数，p＝1为海明距离，p＝2为欧氏距离；m为识别指标数。

当α＝1，p＝1即为线性模型u＝0．515；当α＝1，p＝2时，u＝0．515；当α＝2，p＝1时，u＝0．530；当α＝2，p＝2时，u＝0．530。由于模型的改变，综合相对隶属度0．515变为0．530。综合以上情况，可以组成一个模糊可变集合u＝｛0．515，0．515，0．530，0．530｝。可见模型的改变，u的综合相对隶属度仍处在u的吸引（为主）域中，从工程应用的角度而言，增加了成果的可信性。可取集合u的均值0．523，作为识别的最后成果，即该化石隶属于人的相对隶属度为0．523。已经由猿通过质变点0．5转化为人，但隶属于人的相对隶属度还很低，或隶属于人类的初级阶段。

类似的，可改变模型的参数，如固定模型改变模型中的指标权重，综合隶属度就会有相应的变化，例如把等权重变为w＝（w1，w2，w3）＝（0．4，0．3，0．3），采用α＝1，p＝1的线性模型，u＝0．510。当然可以既改变模型又改变模型中的参数，本例不再详述。

文献［5］可拓集合对指标（1）进行关联函数计算时，由于本例x1＝50，a1＝51，c1＝35，d1＝59，属于本文第1节中所述的情况②，不能应用式（1）计算指标（1）的关联函数，故文献［5］指标（1）关联函数计算值有误，使得文献［5］最后计算结果失去科学性。此外，文献［5］中可拓集合方法的最后计算结果未体现出可拓变化的初衷。

5 结 论

根据本文研究，可以得出以下的结论：①文献［1－8］关联函数公式（1）有误，不能在实际工程领域中应用；②可拓学的基础概念；零（临）界元素、关联函数只是描述客观事物运动发展变化、量变、质变及其转化等自然辩证法概念的表象，而非本质描述。作为研究矛盾问题为主要对象的哲学、数学与工程学相结合的横断新学科，似应加以改进；③差异函数概念是对客观事物运动发展变化、量变与质变，及其转化的本质——吸引与排斥的一种描述，

符合自然辩证法原理；④模糊可变集合概念、理论与方法，是工程模糊集相对隶属度可变理论的发展，提出的模糊可变概念、理论、模型与方法，是笔者在长期水利水电与水文水资源工程实践中提出的理论与工程方法，其基本原理与方法，将继续在实际应用中检验、提高与发展。

［1］蔡 文．可拓论及其应用［J］．科学通报，1999，44（7）：673－682．

［2］CAI Wen．Extension theory and its application［J］．Chinese Science Bulletion，1999，44（17）：1 538－1 548．

［3］蔡 文．可拓集合和不相容问题［J］．科学探索学报，1983，（10）：83－97．

［4］蔡 文．物元模型及其应用［M］．北京：科学技术文献出版社，1994．

［5］蔡 文，杨春燕，林伟初．可拓工程方法［M］．北京：科学出版社，1997．

［6］杨春燕，蔡 文．可拓工程研究［J］．中国工程科学，2000，2（12）：90－96．

［7］蔡 文，杨春燕，何 斌．可拓学基础理论研究的新进展［J］．中国工程科学，2003，5（2）：80－87．

［8］蔡 文．建设一门新的横断学科［C］／／中国人工智能进展（2003）．北京：北京邮电大学出版社，2003．

［9］陈守煜．工程模糊集理论与应用［M］．北京：国防工业出版社，1998．

［10］恩格斯．自然辩证法［M］．北京：人民出版社，1971．

［11］中国科学技术大学．自然辩证法原理［M］．长沙：湖南教育出版社，1986．

［12］孟凯韬．哲理数学基础［M］．北京：中国科学技术出版社，1999．

［13］陈守煜．复杂水资源系统优化模糊识别理论与应用［M］．长春：吉林大学出版社，2002．

［14］CHEN Shou－Yu．Relative membership function and new frame of fuzzy sets theory for pattern recognition［J］．The Journal of Fuzzy Mathematics，1997，5（2）：401－411．

［15］CHEN Shou－Yu．Nonstructured decision making analysis and fuzzy optimum seeking theory for multiobjective systems［J］．Journal of Fuzzy Mathematics，1996，4（4）：835－842．

［16］CHEN Shou－Yu．Fuzzy recognition theoretical model［J］．Journal of Fuzzy Mathematics，1993，1（2）：261－269．

［17］陈守煜．模糊聚类循环迭代理论与模型［J］．模糊系统与数学，2004，18（2）：57－61．

［18］陈守煜，韩晓军，王建明，等．模糊聚类、识别、优选统一理论与循环迭代模型［J］．大连理工大学学报，2004，44（6）：883－886．

［19］陈守煜．工程可变模糊集理论与模型─模糊水文水资源学数学基础［J］．大连理工大学学报，2005，45（2）：308－312．

［20］陈守煜．可变模糊集理论哲学基础［J］．大连理工大学学报：社会科学版，2005，26（1）：1－5．

［21］陈守煜．质量互变定理用于织别可拓学与集对分析的基础性错误［J］．黑龙江大学工程学报，2014，5（1）：1－4．