单级倒立摆的分数阶PIλDμ控制器设计

李明杰，赵志诚，桑 海

(太原科技大学电子信息工程学院，太原 030024)

倒立摆系统是一个复杂的、非线性、多变量、强耦合、不稳定的高阶系统，也是验证各种先进控制策略的典型实验平台。目前针对倒立摆系统控制的方法主要包括 PID 控制[1]、状态反馈控制[2]、模糊控制[3]、拟人智能控制[4]、滑模变结构控制[5]，以及这些控制算法相互结合与集成，而且由倒立摆系统研究产生的控制方法和技术在机器人控制、人工智能、军事领域和一般工业应用等方面都具有广泛的应用开发前景，所以对单级倒立摆系统这样的一个典型被控对象进行研究，无论在理论上和实践中都具有重要的意义。

分数阶微积分理论的建立至今已有三百多年的历史，分数阶微积分就是指微分和积分的阶次可以是任何数或者说可以是分数，常用的整数阶微积分是分数阶的一种特殊形式，但早期主要侧重于理论研究，近年来将分数阶控制理论与PID控制器参数整定理论相结合，分数阶PIλDμ控制已引起众多研究者的关注[6-12]。常规的整数阶PID控制器由于结构简单、易于操作、鲁棒性强等特点，在工业控制领域得到广泛应用。Podlubny教授提出的分数阶PIλDμ控制器具有优于整数阶 PID控制器的性能[13]。两者相比，整数阶PID控制器只是分数阶PIλDμ控制器的特例，分数阶 PIλDμ控制将传统的PID控制推广到分数阶领域，比传统的PID控制多了2个可调参数λ和μ，即积分项和微分项的阶次，因此它具有更大的可调范围和更好的控制品质[14]，为控制系统获得更优性能提供了可能。

1 系统建模及化简

1.1 系统的数学建模

在忽略了空气阻力和各种摩擦之后，可将单级倒立摆系统抽象成小车和匀质杆组成的系统，其结构如图1所示。

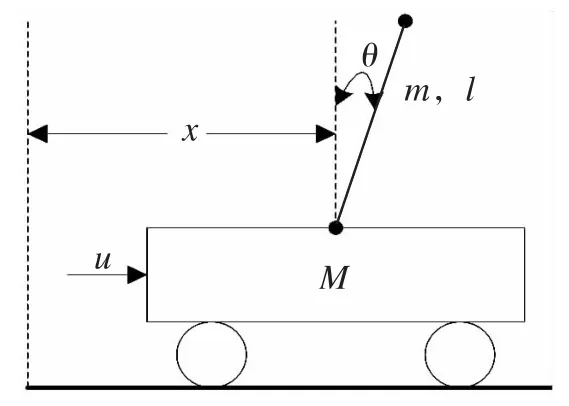
图1 单级倒立摆系统模型Fig.1 Single inverted-pendulum system model

假定系统的相关参数如下:小车质量M=1.096 kg，摆杆质量 m=0.109 kg，小车摩擦系数 b=0.1 N/m/s，摆杆转动轴心到杆质心的长度l=0.25 m，摆杆惯量 I=0.0034 kg·m2，重力加速度 g=9.8 m/s2，u为作用在小车上的力(N)，θ是摆杆与垂线向上方向的夹角(rad)，x是小车运动的水平位移(m).

单级倒立摆系统的控制目标是通过实时给定的控制量u来控制小车的位移x和摆杆的角度θ，使之能够快速的回到倒立的平衡位置。运用牛顿力学定律以及刚体沿定轴转动性质，采用分离法分别对小车和摆杆进行受力分析，建立系统的运动方程:

1.2 模型简化处理

系统在平衡位置附近时摆角θ变化很小(θ≪1 rad)，在此为了把系统的精确模型简化处理，假设摆角θ只在平衡点附近发生细微变化，则可以对系统进行近似处理，此时有dθ/dr≈0、cosθ≈1、sinθ≈θ，将其代入式(1)可得到下面方程组:

设系统的状态空间方程为:

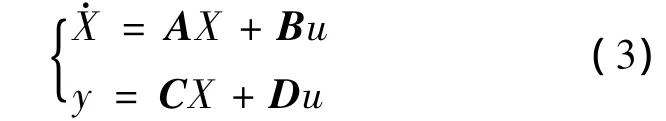
对式(2)进行整理后得系统的状态空间方程:

将系统的参数代入空间状态方程可得:

2 分数阶PIλDμ控制器

将传统的整数阶PID控制器的微分项和积分项的阶次推广到分数域，可得到分数阶PIλDμ控制器如下式:

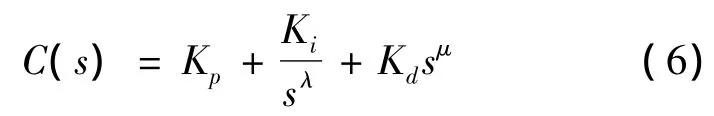
式中，λ和μ分别为分数阶PIλDμ控制器的积分和微分阶次，且均为大于0的任意实数，Kp、Ki、Kd分别为比例、积分、微分增益。由式(6)可以看出当λ=μ=1时，C(s)为PID控制器;当λ =1，μ=0时，C(s)为PI控制器;当 λ =0，μ =1时，C(s)为PD控制器，由此可见整数阶PID控制器为分数阶PIλDμ控制器的特例。

由于分数阶系统微积分的阶次不是整数，只能用微分方程的有限项近似逼近来实现。在采用连续滤波器的多种实现算法中，最常用的当属Oustaloup算法[15]，该方法首先选定拟合频率段 (ω1，ω2)，ω1和ω2分别为拟合频率的下限和上限，则构造的连续滤波器的传递函数模型为:

图2 分数阶PIλDμ控制器结构Fig.2 Structure of Fractional-order PIλDμ controller

3 分数阶PDμ控制器设计

由数学模型可知，单级倒立摆是一个单输入(小车受到外力F)双输出(摆杆角度θ和小车运动的水平位移x)的被控对象，为此本文提出双回路分数阶PDμ控制方案，其原理如图3所示，这样可对系统的两个被控变量同时进行闭环调节，实现倒立摆的稳定控制。

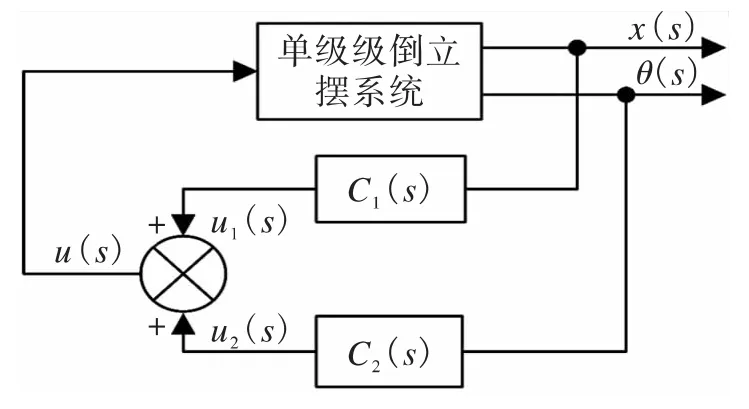
图3 双回路控制原理图Fig.3 The scheme of double-loop control system

由图3所示控制系统总的控制律u是两个单回路控制律之和，即u(s)=u1(s)+u2(s).对控制系统结构分析可知，由控制系统的输出变量来构成闭环反馈控制，得输出反馈控制系统如图4所示，其中，H为输出反馈控制器矩阵。

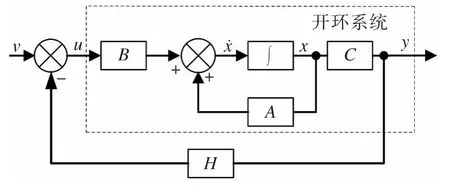
图4 输出反馈系统结构Fig.4 Structure of output feedback system

针对此系统的设计合适的输出反馈控制器，使闭环系统稳定，同时使两个回路都有良好的动态特性。由图4可知输出反馈控制可以视为当K=HC时的状态反馈控制。

考虑系统的稳定性和各种性能指标很大程度上与闭环系统的极点分布有关，因此，在进行控制系统设计时，应将闭环系统的极点配置在期望的位置。这样通过输出反馈控制器来改变控制系统的极点位置可使闭环系统具有所期望的动态特性，使闭环系统渐进稳定，满足设计要求。

由图4可知，若两个回路的控制器为分数阶PDμ控制器的传递函数分别C1(s)=kp1+kd1sα和C2(s)=kp2+kd2sβ，输出反馈控制器矩阵 H= [kp1+kd1sα，kp2+kd2sβ]，其中0 ＜ α、β ＜ 2.可得系统的特征多项式为:

式中，a*=-a，b*=ekp1+fkp2-d，c*=(ceaf)kp2+(ad-cb)，d*=ekd1，e*=(fb-ed)kd1，f*=fkd2，g*=(ce-af)kd2，h*=(fb-ed)kp1;a=-0.0883167，b=0.629317，c=-0.235655，d=27.8285，e=0.883167，f=2.35655.

本文的目的是设计一个输出反馈控制器，能使系统特征多项式所指定的极点都在稳定区域内，使系统达到渐进稳定，所指定的极点不仅要改善系统的性能品质而且同时要使整个系统达到渐进稳定。

对于在复平面s上的一点s=σ+jω的分数阶γ次方有:

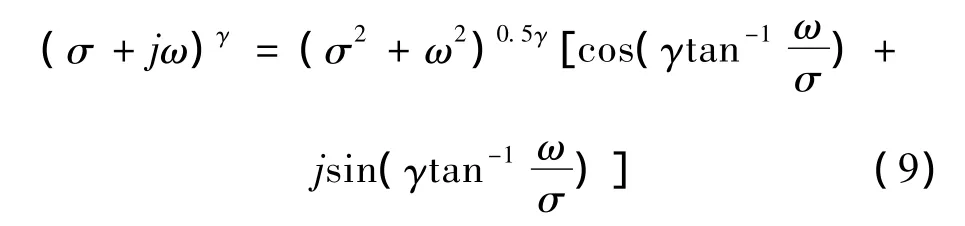
假设闭环系统期望的最大超调量Mp=10%和上升时间 t=0.5 s，得 ζ=0.65，ω0=2.15，这样得到闭环系统的主导极点为 s1，2=-1.432 ± j1.671，将s1=-1.432+j1.671代入式(8)所示的特征多项式得:

式中，R(kp1，kd1，kp2，kd2，α，β)和 I(kp1，kd1，kp2，kd2，α，β)分别表示主导极点 s1=-1.432+j1.671处f(s)的实部和虚部。

利用微粒群优化算法(PSO)对控制器参数进行寻优，选择优化性能指标为:

式中，P=tan-1(I/R)，其参数取值 -200≤kp1，kd1≤0;1 ≤kp2，kd2≤500;0 ≤ α，β ≤2;种群数K=30，学习因子 C1=C2=1.5，惯性权值 ω =0.8.

4 仿真研究

设小车位移x的初始值为0.1 m，摆杆角度θ的初始值为0.05 rad，仿真时间为10 s，仿真步长为5 ms，采用微粒群优化算法得到控制器参数kp1=-15.5326，kd1=-22.6401，kp2=137.5812，kd2=25.9820，α =0.8952，β =1.0384;同时，当控制器为整数阶PD控制器时，即α=β=1时kp1=-55.4252，kd1=-26.4270，kp2=103.8714，kd2=19.2023.系统仿真结果如图5、图6所示。

图5 小车位移响应曲线Fig.5 Response curve of cart displacement

从仿真曲线可以看出，使用分数阶PDμ控制器小车的位移在较短的时间达到稳定状态，而且超调小;摆杆角度响应速度快，超调小。

图6 摆杆角度响应曲线Fig.6 Response curve of swing link angle

5 结论

采用双回路控制系统构建输出反馈闭环控制系统，将分数阶PDμ控制器应用到单级倒立摆系统，研究了输出反馈分数阶控制器的设计问题。仿真结果表明，对于单级倒立摆系统，双回路分数阶PDμ控制较整数阶PD控制，收敛速度快，振荡小，能取得更好的控制效果。

[1]杨世勇，徐莉萍，王培进.单级倒立摆的PID控制研究[J].控制工程，2007，14(s):23-25.

[2]杨平，徐春梅，王欢，等.直线型一级倒立摆状态反馈控制设计与实现[J].上海电力学院学报，2007，23(1):21-25.

[3]侯涛，范多旺，杨剑锋.基于T-S型的平面倒立摆双闭环模糊控制研究[J].控制工程，2012，19(5):753-756.

[4]司昌龙，张明廉.拟人智能控制及控制律转化研究[D].北京:北京航空航天大学，2003.

[5]张志强，李战明.基于模糊滑模变结构的倒立摆控制方法研究[D].兰州:兰州理工大学，2008.

[6]ARIJIT BISWAS，SWAGATAM DAS，AJITH ABRAHAM.Design of fractional-order PIλDμcontrollers with an improved differential evolution [J].Engineering Applications of Artificial Intelligence，2009，22(2):343-350.

[7]CAO JUNYI，CAO BING GANG.Digital realiation and characteristics of fractional order controllers[J].Control Theory and Applications，2006，23(5):792-793.

[8]ZENG QINGSHAN，CAO GUANGYI，ZHU XINJIAN.Analysis of the effect on control of order variation for fractional-order PIλ-Dμcontrollers[J].Journal of Harbin Institute of Technology，2005，12(3):336-340.

[9]DINGYU XUE，CHUNNA ZHAO，YANGQUAN CHEN.Fractional order PID control of a DC-motor with elastic shaft:A case study[C]∥Proc of the 2006 American Control Conf.Minneapolis，2006:3182-3187.

[10]严慧，于盛林，李远禄.分数阶PIλDμ控制器参数设计方法—极点阶数搜索法[J].信息与控制，2007，36(4):445-450.

[11]李大字，刘展，靳其兵，等.分数阶控制器参数整定策略研究[J].系统仿真学报，2007，19(19):4402-440.

[12]梁涛年，陈建军.分数阶参数不确定系统的PIλ控制器[J].控制理论与应用，2011，28(3):400-40.

[13]Chen Y Q，MOORE K L，Vinagre B M，et al.Robust PID controller autouning with a phase shaper[M].Augsburg，Germany:UBooks，2005:687-706.

[14]PODLUBNY I.Fractional-order systems and PIλDμcontroller[J].IEEE Transactions on autouning Controller，1999，44(1):208-214.

[15]OUSTALOUP A，LEVRON F，MATHIEU B，et al.Frequency-Band Complex Noninteger Differentiator:Characterization and Synthesis[J].IEEE Transaction on Circuit and Systems-I:Fundamental Theory and Applications，2000，47(1):25-39.