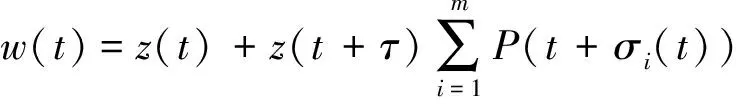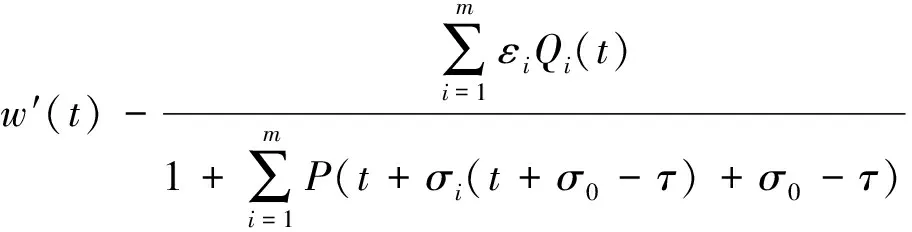非线性中立型变时滞微分方程解的零点分布
2014-06-13孟智娟
孟智娟,杨 军
(1.太原科技大学应用科学学院,太原 030024;2.燕山大学理学院,河北 秦皇岛 066004)
近年来,对时滞微分方程和中立型微分方程振动解的零点分布及零点个数进行了许多研究[1-10],并获得了许多很多的结论,但几乎都是对单个常时滞线性微分方程的零点距进行了估计,对具有多个变时滞非线性微分方程振动解的零点分布研究结果寥寥无几,本文考虑微分方程:

(1)
其中:
P(t),Qi(t),σi(t)∈C([t0,+∞],R+),τ∈R+
(2)

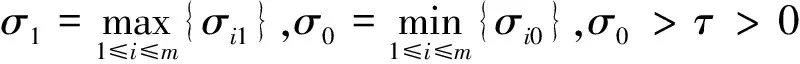
解的零点分布,对其相邻零点间的距离进行了估计,并改进和推广了已有的一些的结果。
1 引理
首先,如文献[3]中,定义序列{an(ρ)},0<ρ<1,如下:
a0(ρ)=1,an+1(ρ)=eρan(ρ),n=1,2,…
(3)

(4)
再定义序列{bm(ρ)},0<ρ<1如下:

(5)
易证,0<ρ<1时,bm+1(ρ) (6) 为了证明本文的结论,我们用到以下的引理。 考虑微分不等式: (7) 引理1假设Qi(t),σi(t)∈C([t0,+∞],R+),i=1,2,…,m,x(t)是不等式(7)在[t0,+∞]上的解,若存在t1≥t0,0<ρ<1,使得: (8) 且存在T0≥t1,T≥T0+3σ1,使x(t)在[T0,T]上恒为正,则对任意n≥1,T-(2+n)σ0≥T0有: (9) 证:由(7)得: (10) 故x(t)在[T0,T-σ0]上不减,因此有: (11) 当T0≤t≤T-3σ0时,式(7)两边除以x(t)并从t到t+σ0积分得: (12) ρa0(ρ) 引理2假设Qi(t),σi(t)∈C([t0,+∞),R+),i=1,2,…m,x(t)是不等式(7)在[t0,+∞)上的解,若存在t1≥t0,0<ρ<1,使得: (13) (14) 且存在T0≥t1+σ1,正整数N≥4使x(t)在[T0,T0+Nσ0]上恒为正,则对任意m≤N-3有: (15) t1+σ0 (16) 由t-σ0≤s≤t,知t≤s+σ0≤t+σ0≤T0+(N-2)σ0,(7)式从t到s+σ0积分得: 由(10)式知x(u+σi(u))在T0≤u≤T0+(N-2)σ0上不减,联立(14)式得: (17) 由(16),(17)两式得: 因x(λt)≤x(t),则: (18) 又t∈[T0+σ0,T0+(N-3)σ0]时,x(t-σ0)>0,由(18)式得: (19) 当T0+2σ0≤t≤T0+(N-3)σ0时,易知T0+σ0≤t-σ0≤T0+(N-4)σ0,由(19)得: 代入(18)式得: 因此: 重复上述过程,得: (20) 定理1假设(2)成立,且Qi(t),σi(t)是以τ为周期的函数。 (21) 记Ri(t)=P(t+σi(t)),i=1,2,…,m P(t)∈C′([t0,+∞),R+), (22) 且存在t1≥t0使得: (23) 则对任意T≥t1,方程(1)在[T,T+3σ0-τ]上至少存在一个零点。 证明:否则,不失一般性,设方程(1)的解x(t)>0,t∈[T,T+3σ0-τ]为方便起见,下记: z(t)=x(t)+P(t)x(t+τ) (24) 则z(t)>0,t∈[T,T+3σ0-2τ] (25) (26) (27) (28) 则w(t)>0,t∈[T,T+3(σ0-τ)] (29) (30) 由式(26)和式(28)知: t∈[T,T+2(σ0-τ)] 由式(30)知: 则有: (31) (31)式从T到T+σ0-τ积分得: w(T+σ0-τ)≥w(T)+w(T+σ0-τ) 即w(t)≤0,产生矛盾,证毕。 定理2假设式(2),式(21),式(22)成立,存在t1≥t0和正常数ρ,1/e<ρ<1,使得: 进一步设: t1≤t≤s+σ0-τ≤t+σ0-τ 则对任意的T≥t1+σ0-τ,方程(1)的解x(t)在[T,T+2σ0+K(σ0-τ)]上至少存在一个零点,这里: 定理3假定式(2),式(21),式(22)和式(33)成立,且存在t1≥t0和正常数ρ,0<ρ≤1/e,使(32)式成立,进一步假设存在序列{Ti},Ti→∞,i→+∞使得: 其中a(ρ)是方程(4)在[1,e]上的实根. 定理2,定理3证明略,由引理1,引理2及定理1容易得证,事实上,定理1,2,3给出了方程(1)解振动的充分条件。 参考文献: [1] 李秉团.一阶时滞微分方程解的零点距估计[J].应用数学学报,1990,13(4):467-472. [2] 林诗仲.一阶中立型微分方程解的零点估计[J].应用数学学报,1994,17(3):458-461. [3] 周勇,刘正荣,俞元洪.中立型时滞微分方程解的零点距估计[J].应用数学学报,1998,21(4):505-512. [4] 于江.一阶时滞型微分方程解的零点距估计[J].山西大学学报,1995,18(2):134-137. [5] LIANG FAXUN.The Distribution of zeros of Solutions of First-Order Delay Differential Equations[J].Mathematical Analysis and Applications,1994,186:383-392. [6] ZHOU YONG.The Distribution of zeros of Solutions of First-Order Neutral Differential Equations[J].Northeast Math J,1997,13(2):153-159. [7] ZHOU YONG.An Estimate for Distance Between Adjacent Zeros of Solutions of Neutral Equations[J].Chinese Quarterly Journal of Mathematics,1996,11(4):38-43. [8] HAIPING YE,GUOZHU GAO.The Distribution of Zeros of Solutions of Neutral Advanced Differential Equations[J].Applied Mathematics Letters,2004,17:997-1005. [9] 闫信州,曹秀梅,姜德民,等.时间标度上的一阶时滞型微分方程解的零点距估计[J].莱阳农学院学报,2006,23(2):150-153. [10] CHEN YU.Estimates of the zeros and Growths of Meromorphic Solutions of Homogeneous and Non-homogeneous second order Linear Differential Equations[J].Mathema Tica Applicata,2010,23(1):18-26.


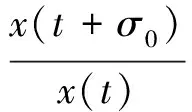

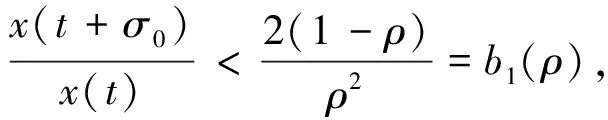



2 主要结果