一种四阶P-Laplace图像盲复原方法
2014-10-16王国宇姬婷婷
刘 琨,王国宇,姬婷婷
(中国海洋大学信息科学与工程学院,山东 青岛266100)
图像在形成、传输和存储过程中不可避免地引起图像质量的退化,如成像系统的缺陷、外部干扰等等。在成像系统为线性平移不变系统的假定下,可用如下模型来描述退化的图像[1]:

其中:u(x,y)表示理想图像;h(x,y)表示成像系统的点扩散函数;n表示图像的加性噪声;u0(x,y)为退化模糊图像;表示卷积操作。
图像盲复原问题是图像处理问题中的经典问题之一,近年来图像盲复原算法得到了广泛的研究。图像复原算法大致可以分为两类:一类是先辨识点扩散函数,再利用传统的复原算法进行复原;另一类是同时估计点扩散函数和原始图像。目前成功的算法以Kundur等人提出的利用非负和有限支撑约束的递归逆滤波盲图像恢复算法(NAS-RIF)[2]以及 Rudin、Chan等人提出的全变分(TV)正则化盲图像恢复算法[3-5]最为典型。而NAS-RIF算法由于需预先知道图像的支持域,且算法对噪声敏感等原因,致使应用受到限制。全变分正则化盲图像恢复算法较为成功,但由于该算法采用的是二阶偏微分方程模型,在复原图像的同时容易引起阶梯效应。基于偏微分正则化方法同时估计点扩散函数和原始图像方法中,以You和Kaveh提出的二阶偏微分[6]以及Chan和 Wong提出的偏微分盲图像复原方法[4]最为典型。但是You和Kaveh提出的算法容易引起图像模糊,而Chan和Wong提出的算法容易引起阶梯效应。P-Laplace方法[7]相对于以上方法有了很大改进,但复原出来的图像仍然不够理想。
为了克服阶梯效应和模糊问题,很多学者做了广泛研究[7-9],虽然 P-Laplace方法在对图像边缘和内部平滑区域做分别处理时对TV复原方法中出现的阶梯效应有一定的缓解作用,但仍然不够理想。本文在不改变图像演化方程基本性质的基础上改进P-Laplace方法,引入参数λ调节复原过程中的保真项并对偏微分方程做单调灰度变化,进一步缓解了阶梯效应,但通过大量的实验验证,改进的P-Laplace方法存在的阶梯效应问题仍然会对图像清晰度产生影响。在此考虑到四阶偏微分方程模型较二阶模型在去除噪声和保持边界的同时,能更好地避免阶梯效应[10-12],本文提出了一种四阶P-Laplace偏微分图像复原方法,引入了新的能量泛函,进一步避免阶梯效应以提高复原图像质量。实验结果证明,该算法相比于TV和P-Laplace复原方法,对模糊图像有更好的复原效果,同时也适用于水下图像和雾天图像的图像复原。
1 P-Laplace图像盲复原模型

其中:α1,α2是正的参数;p(u)为扩散控制因子,取值范围为其值由等照度线的曲率k和梯度模值共同决定:

2 四阶P-Laplace图像盲复原
在以上P-Laplace图像盲复原模型的基础上,对于(6)式中的ut,将右边乘以梯度模值u ,便得
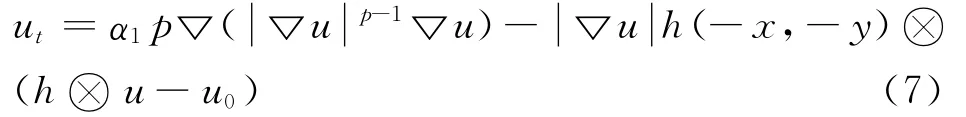
由于单调灰度变换不改变图像演化的方程的基本性质[8],因而改进的模型(7)是近似满足形态学原则的,但这种改进会使阶梯效应得到有效的缓解。
不少学者在克服由TV正则化所产生的阶梯现象时,提出了一种有效的采用高阶范数来度量图像的方法[10-12]。考虑到四阶偏微分方程模型在去除噪声和保持边界的同时能避免阶梯效应,将四阶偏微分方程引入,本文提出一种四阶P-Laplace图像盲复原方法,能量泛函表示如下:
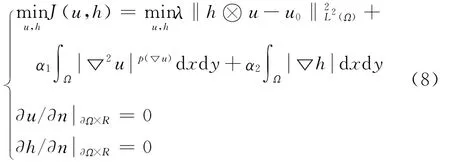
其Euler-Lagrange方程为:
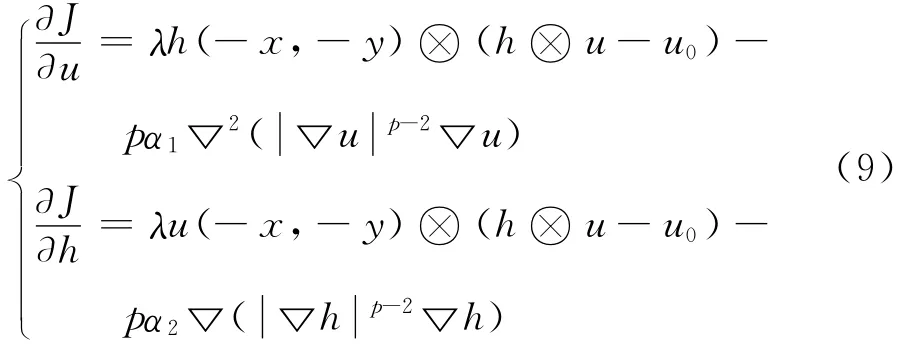
通过梯度下降流法,将模型的求解转化为非线性反应扩散方程组,并进行单调灰度变换得:
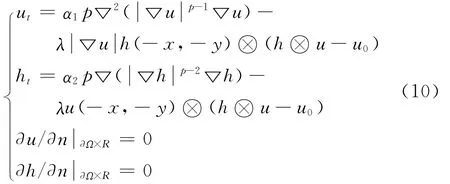
初始值u(x,0)=u0(x)满足周期性条件。
由于满足平面方程的图像,其强度函数的Laplace算子为零并满足Euler-Lagrange方程,因此一个平面图像就是一个不动点,由此平面图像就是式(9)的全局最小解[10]。采用四阶偏微分方程的最大优点是由于它用分片平面图像来近似边界,从而消除了二阶非线性扩散所造成的阶梯效应。
同时,四阶P-Laplace图像盲复原模型中引入参数λ调节复原过程中的保真项,在保证复原效果的前提下,减少复原过程中的计算量。
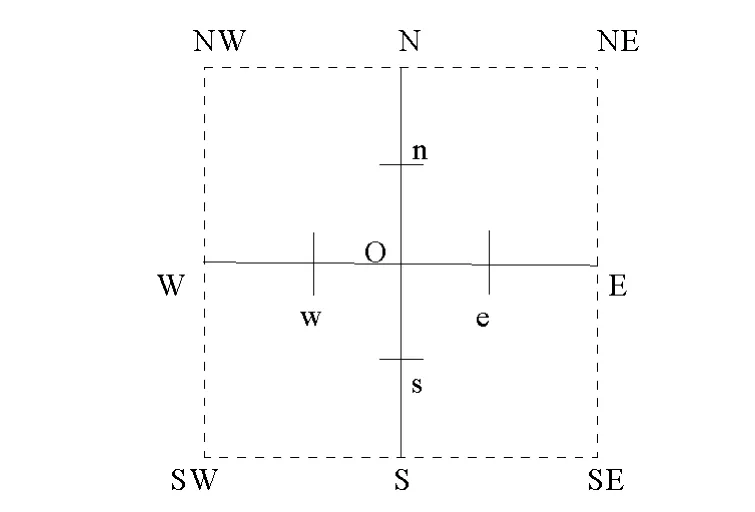
图1 待修复像素及邻域点示意图Fig.1 Pixels under repaired and neighborhood point
3 数值计算方法
这里采用差分的数值计算方法,将图像离散化,记h为空间步长,u(xi,yi,tn)记为uni,j,则ut估计用差分格式:
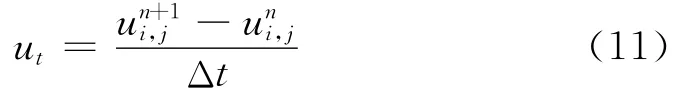
其中Δt是时间步长,用中心差分进行估计:
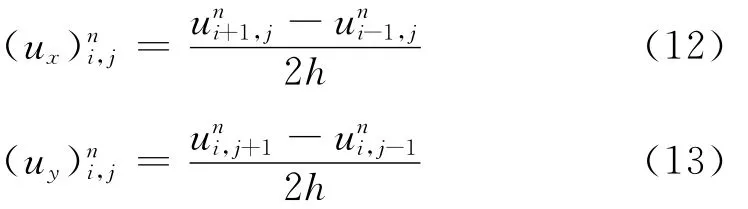
对于散度算子,这里采用半点中心差分法实现。如图1所示,待修复点为O,N、S、W、E为O的4个邻域点,n、s、w、e分别为对应的4个邻域半点。令:
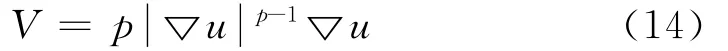
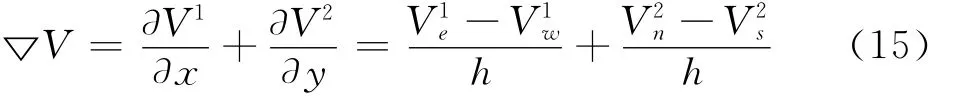
由于半点值不能直接得到,以eS点为例求解如下:

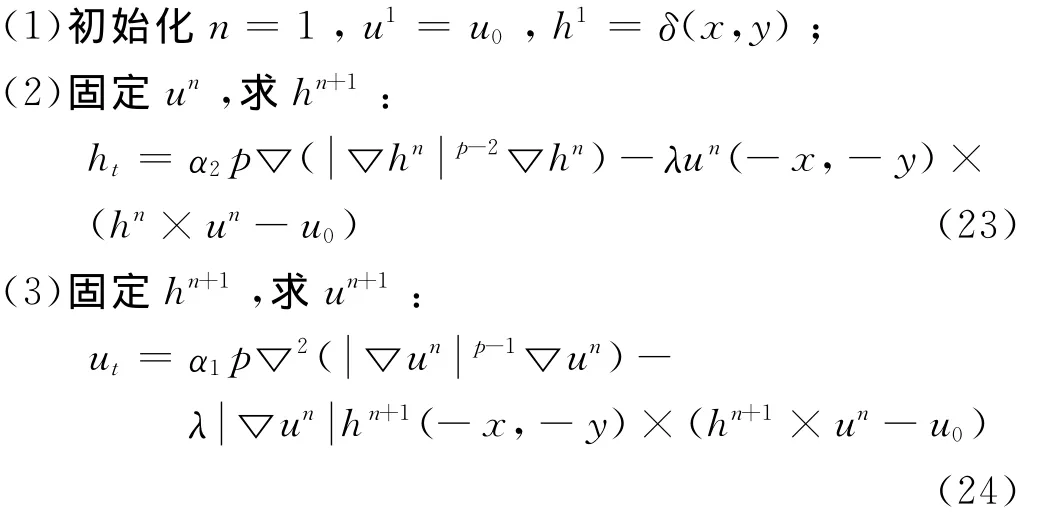
如此交替公式(23)和(24)的迭代,根据迭代次数,最终得到复原图像。
4 实验结果和分析
4.1 本文方法与其他方法的对比分析
为了验证本文算法的正确性和有效性,采用大小为256×256像素的Lena标准灰度图像作为测试图像,分别对无噪模糊图像和带有不同程度噪声的模糊退化图像进行复原。模糊的退化图像是利用二维高斯函数卷积核进行模糊化,噪声是高斯白噪声。实验分别比较了TV复原方法、P-Laplace方法和本文方法。
实验中,标准Lena图像通过7×7的高斯点扩散函数进行模糊,高斯白噪声均值为0、标准差分别取2、4、6…16,交替迭代次数为100次,参数λ=1.5,正则化约束参数α1=α2=0.002。图2为Lena清晰图像,图3中的4幅图为无噪模糊图像以及分别采用TV复原方法、P-Laplace方法和本文方法复原模糊图像(见图3(a))的效果图;图4中的4幅图为带噪模糊图像(高斯白噪声标准差为6)以及分别采用TV复原方法、P-Laplace方法和本文方法复原带噪模糊图像(见图4(a))的效果图。

图2 Lena清晰图像Fig.2 The sharp image Lena

图3 无噪模糊图像以及图像恢复结果Fig.3 The blurred image without noise andimage restoration results

图4 带噪模糊图像以及图像恢复结果Fig.4 The blurred image with noise and image restoration results
从图3、4可以看到,不管是无噪模糊图像还是带噪模糊图像,视觉效果上TV方法的复原效果一般,PLaplace方法的复原效果有明显改进,而本文方法的复原效果最好。用峰值信噪比PSNR值作为评价标准,表1为无噪模糊图像以及3种复原方法复原结果的PSNR值,图5为带噪模糊图像(带有不同程度噪声)以及3种复原方法复原结果PSNR值的走势图。
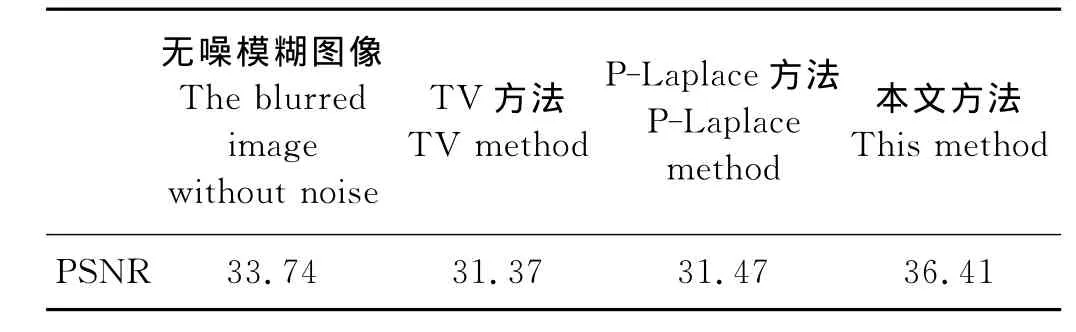
表1 无噪模糊图像的复原评价Table 1 The evaluation of blurred image restoration without noise
表1显示,对无噪模糊图像的复原中,本文方法的PSNR值最大,有明显的复原效果并且优于TV方法和P-Laplace方法。从图5可以看出,当噪声程度较低时,本文方法的PSNR值远远大于带噪模糊图像以及其他方法的复原结果,说明本文方法的复原效果是最好的。

图5 不同程度带噪模糊图像的复原评价Fig.5 The evaluation of blurred image restoration with noise in different level
4.2 本文方法与P-Laplace方法的对比分析
为了进一步验证本文方法相比较传统P-Laplace方法的优越性,实验又采用大小为256×256像素的Lady图像作为测试图像,分别对无噪模糊图像和带有不同程度噪声的模糊退化图像进行复原。模糊的退化图像是利用二维高斯函数卷积核进行模糊化,噪声是高斯白噪声。实验详细比较了P-Laplace方法和本文方法。
实验中,Lady图像通过7×7的高斯点扩散函数进行模糊,高斯白噪声均值为0、标准差分别取2、4、6、8,交替迭代次数为150次,参数λ=1.5,正则化约束参数α1=α2=0.002。图6为Lady清晰图像,图7中的两幅图分别为无噪模糊图像和带噪模糊图像(高斯白噪声标准差为2),图8中的两幅图为分别采用P-Laplace方法和本文方法复原无噪模糊图像(见图7(a))的效果图;图9中的两幅图为分别采用P-Laplace方法和本文方法复原带噪模糊图像(见图7(b))的效果图。

图6 Lady清晰图像Fig.6 The sharp image Lady

图7 无噪模糊图像以及带噪模糊图像Fig.7 The blurred image without noise and the blurred image with noise
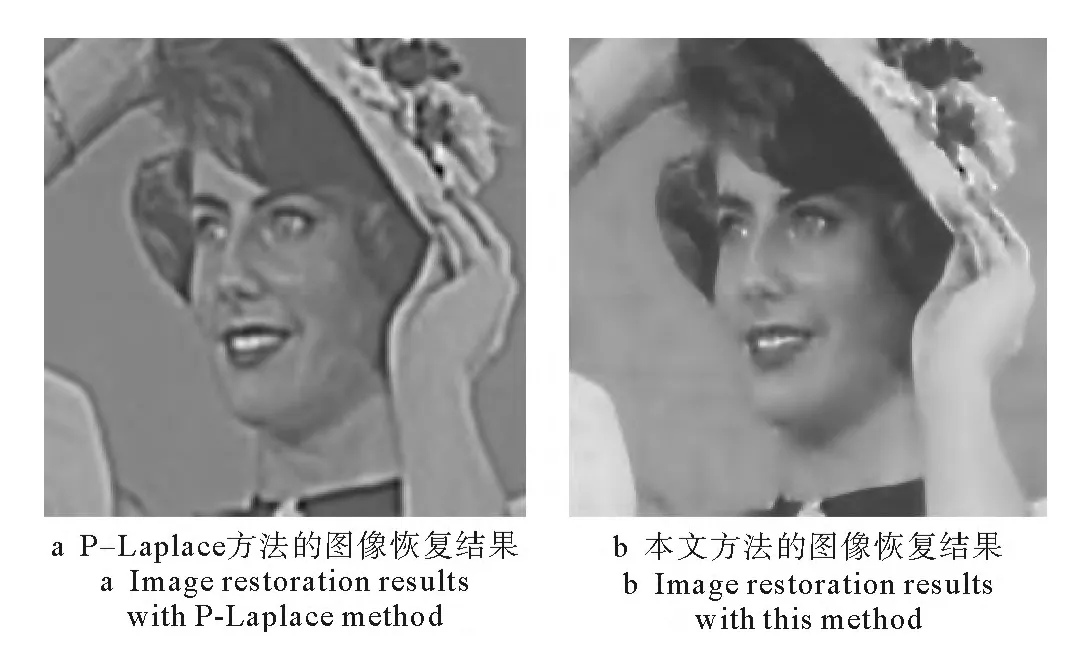
图8 对无噪模糊图像的图像恢复结果Fig.8 Image restoration results on the blurred image without noise

图9 对带噪模糊图像的图像恢复结果Fig.9 Image restoration results on the blurred image with noise
从图像恢复结果可以看出,在主观视觉上,不管是对无噪模糊图像的复原还是对带噪模糊图像的复原,P-Laplace方法的复原结果中都能看到明显的阶梯效应问题,而本文方法在去除噪声和保持边界的同时能避免阶梯效应,相比较P-Laplace方法,本文方法有很好的复原效果。用峰值信噪比PSNR值作为评价标准,对无噪模糊图像复原时,P-Laplace方法的PSNR值为26.75,而本文方法的PSNR值为30.36,复原效果明显优于P-Laplace方法,表2统计了带噪模糊图像(带有不同程度噪声)以及两种方法复原结果的PSNR值,可以看出,在相同程度噪声干扰下,本文方法比PLaplace方法的PSNR值大,相比较P-Laplace方法有明显的复原效果。
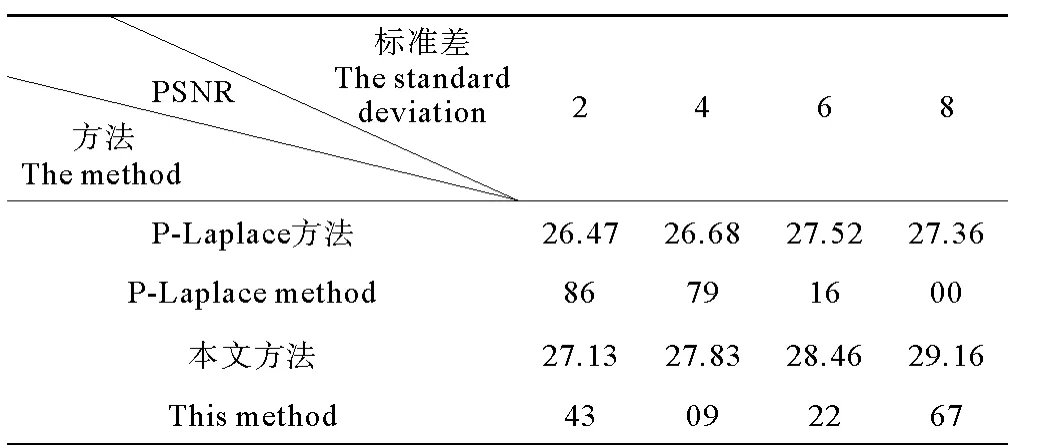
表2 带噪模糊图像的复原评价Table2 The evaluation of blurred image restoration with noise
4.3 本文方法的普适性研究
为了验证本文算法的普遍性和有效性,实验中又分别采用大小为512×512像素的Lena标准灰度图像、水下图像(见图10)和雾天图像(见图11)做测试,复原效果如下图显示。

图10 水下图像的图像恢复结果Fig.10 Image restoration results of the underwater picture

图11 雾天图像的图像恢复结果Fig.11 Image restoration results of the fog image
从水下图像和雾天图像的恢复结果看,经过本文方法的图像恢复处理,可以清楚地看到原来模糊图像中看不清的细节,整幅图像的清晰度也有了很大的提高,在主观视觉上本文方法有很好的复原效果,说明本文方法也适用于水下图像和雾天图像的图像复原。
5 结语
本文提出的四阶P-Laplace图像盲复原方法能够很好地避免阶梯效应,对退化图像的图像恢复有很好的复原效果,特别是对加性噪声比较小的模糊图像的图像复原。同时,本文方法还适用于水下图像和雾天图像。本文方法虽然在保持边界和细节复原方面相比其他方法有很好的效果,但从带有不同程度噪声的模糊图像的图像恢复结果看(见图5),在噪声程度比较大时,本文方法的复原效果一般,因此对于噪声程度较大的退化图像,本文方法还有待进一步改进。
[1] Kurdur D,Hatzinakos D.Blind image deconvolution [J].IEEE Signal Processing Magazine,1996,13(13):43-64.
[2] Kurdur D,Hatzinakos D.Blind image restoration via recursive filtering using deterministic constraints [C].//Proceedings of the 1996IEEE International Conference on Acoustics.Atlanta :Speech and Signal Processing,1996:2283-2286.
[3] Rudin L I,0sher S,Fatima E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1):259-268.
[4] Chan T,Wong C.Total variation blind deconvolution [J].IEEE Transactions on Image Processing,1998,7(3):370-395.
[5] Chan T,Wong C.Convergence of the alternating minimization algorithm for blind deconvolution[J].Linear Algebra and Its Application,2000,316(3):259-285.
[6] You Y,Kaveh M.Blind image restoration by anisotropic regularization [J].IEEE Transactions on Image Processing,1999,8(3):396-407.
[7] 陈建军.基于偏微分方程的图像降噪和图像恢复研究 [D].重庆:重庆大学,2009.
[8] 王大凯,侯榆青.图像处理的偏微分方程方法 [M].1版.北京:科学出版社,2008:147-151.
[9] 马少贤,江成顺.基于四阶偏微分方程的盲图像恢复模型 [J].中国图象图形学报,2010,15(1):26-30.
[10] You Y,Kaveh M.Fourth-order partial differential equations for noise removal[J].IEEE Transactions on Image Processing,2000,9(10):1723-1730.
[11] Chan T,Marquina A,Mulet P.High-order total variation based image restoration [J].SIAM Journal on Scientific Computing,2000,22(2):503-516.
[12] You Y,Kaveh M .Image enhancement using fourth order partial differential equations [C].//Proceedings of the Thirty-Second Asilomar Conference on Signals.Pacific Grove:Systems & Computers,1998:1677-1681.
