大直径浮式结构涡激振动的数值模拟*

周 阳，黄维平

（中国海洋大学山东省海洋工程重点实验室，山东 青岛266100）

对涡激振动的研究由来已久，主要针对物体在一定速度的流体中，其尾流产生交替的涡泄，导致物体两侧压强的交替变化，从而引起结构的振动，对于Spar平台等大直径浮式结构，尾流的涡旋脱落周期较长，且其自身刚度远远大于系泊系统的刚度，发生涡激振动时，其运动幅度以壳体的整体运动为主，这种振动称为涡激运动（Vortex－Induced Motion，VIM）。目前海洋工程方面，主要是针对立管和海底管线等大长细比的柔性结构进行涡激振动研究［1－2］。但是，对于Spar平台这种大型新型海洋结构物的涡激运动研究才刚起步［3－7］。国际上已有一些学者对涡激运动进行了运动特性研究［8－10］，其中包括侧重于工程应用角度的对海洋平台等结构物进行的涡激运动整体预报的相关研究［8－9］，还包括侧重于考察非流线型柱状主体周围的复杂流动现象、涡的生成和脱落特征方面的机理性研究［10］。

涡激运动包括横流向和顺流向的两向涡激运动。大部分软件对涡激运动进行计算时，会忽略流固耦合的作用，即使考虑流固耦合，也只是考虑结构位移对流场变化带来的影响，而不考虑结构速度带来的影响，即非线性阻尼带来的影响。为了更好的研究流固耦合对于Spar平台两向涡激运动的影响，本文运用Matlab程序分别对Spar平台顺流向和横流向涡激运动进行了流固耦合数值模拟，探讨结构速度和两向涡激运动之间的关系，并对结构非线性阻尼的影响进行了探讨。

1 模型介绍

本文主要针对一硬舱外径为28m，长为70m，连接段外径为14m，长为84m，软舱外径为28m，长为15m的简易Spar平台模型进行分析，其中干舷为16m（见图1）。系泊系统由9根系泊缆组成，9根系泊缆分成3组对称布置（见图2），其水平刚度为93.745kN／m。进行了流速为0.2～2m／s的情况下的两向涡激运动的数值模拟。

图1 Spar平台模型Fig.1 Model of Spar platform

2 数值模拟方法

本文将Spar平台看做刚体进行整体分析，运用Matlab软件根据Newmark－β法编程完成平台的两向涡激运动响应计算［11］。

图2 Spar平台系泊系统平面布置Fig.2 Floorplan of Spar mooring system

2.1 数模建立

由于数值模拟的需要，需要对模型进行简化，并引入一些假定。

平台所受涡激升力包括两部分，一部分为硬舱和软舱涡泄时产生的两向涡激升力，由于直径相同，因此升力频率一样，故对于平台的受力可以叠加在一起进行。另一部分为连接段涡泄时产生的两向涡激升力，由于直径与硬舱和软舱不同，因此其涡泄升力频率不一样，其作用力要单独加在平台上。

由于研究平台涡激运动时，只考虑水平面内的运动，因此系泊系统的刚度只考虑其水平刚度，由于位移比较小，同时忽略了平台产生位移时对系泊系统水平刚度的影响，将水平刚度视为一个定值。

由于Spar平台自上而下不是均匀的圆筒形，其涡激升力沿高度方向也不统一，因此，实际过程中，平台会发生一定的横摇和纵摇，为了计算需要，本文同时忽略了平台发生横摇和纵摇时对此次数值模拟的影响。

2.2 Newmark－β法参数选定

Newmark－β法中，根据拉格朗日中值定理，t＋Δt时刻的速度表示成

于是t＋Δt时刻的速度

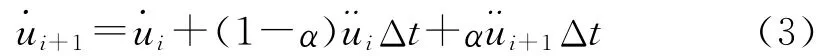
由泰勒级数导出

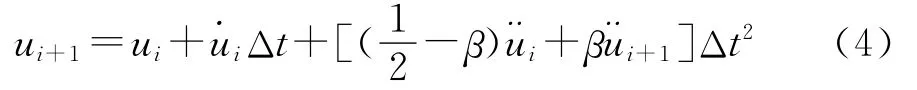
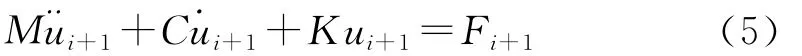
利用式（3）和（4），写出t＋Δt时刻的速度和加速度的表达式

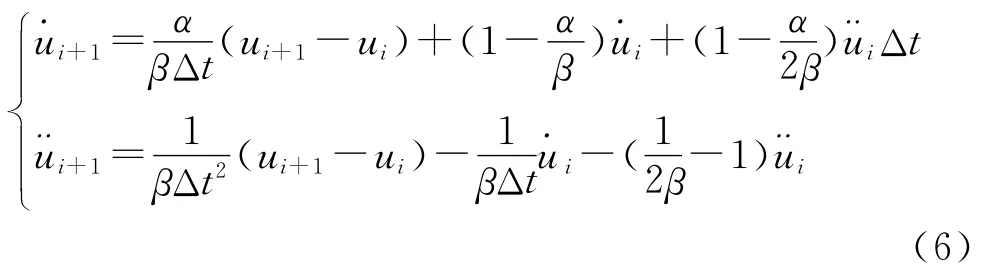
把式（6）代入（5）并消去lui＋1和¨ui＋1得到关于ui＋1的求解方程

其中

求解方程（7）得到ui＋1，然后根据公式（6）可求得

根据上面建立的迭代公式，可归纳出Newmark－β法的计算过程：第一步形成K＊，第二步根据F＊i＋1求解方程（7）得到位移响应ui＋1，并按照式（6）求速度和加速度响应。逐步进行迭代即可得到整个时间段的响应情况，这是一种数值解的方法。在此次计算中，取α＝

3 流固耦合时两向涡激运动的数值模拟

3.1 考虑非线性阻尼时顺流向涡激运动响应

平台的顺流向涡激运动是指涡旋脱落时对平台引起沿着来流方向的曳力，导致平台产生沿流方向的往复运动，相关圆柱形平台的运动方程如下：

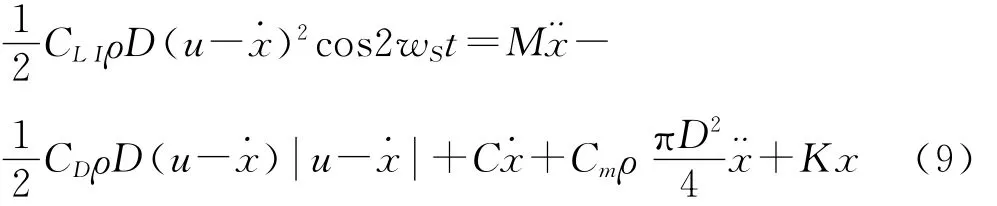
式中：CLI为脉动拖曳力系数，与Re有关；u为来流速度；x为立管顺流向振动位移；lx为立管顺流向振动速度为立管顺流向振动加速度；wS为涡泄频率；M为单位长度质量；K为单位长度锚链水平刚度；C为结构阻尼；Cm为附加质量系数；CD为拖曳力系数。其中根据文献［3，6］，选定CLI为0.05，CD为1.4，Cm为1。涡泄圆频率其中St为斯托哈尔数，取0.25。

本文提及的非线性阻尼项指的是由于平台和流体之间的相对运动而引起的拖曳力项，对于顺流向的情况，非线性阻尼项为

由于Spar平台中间段，硬舱和软舱的直径不同，计算时将中间段的涡激升力以及硬舱和软舱的涡激升力根据式（9）沿长度方向积分分别加载于平台之上，附加质量力也如此处理。而与平台质量相关的惯性力，总平台结构阻尼以及总锚链水平刚度则以实际Spar平台的参数为准进行加载，其中Spar平台总质量为38 000t，总结构阻尼为4.18×105kg·s－1，总锚链水平刚度为93.745kN／m。此文对于Spar平台的涡激运动数值模拟均采用这种加载方式进行。

根据Newmark－β法对平台的运动方程进行编程计算，分析Spar平台考虑流固耦合时在流速0.2～2m／s工况中，由于涡泄引起的顺流向振动响应。平台的位移以幅值比的形式给出，即位移比硬舱直径的形式，同时计算流速度以约化速度的形式给出（见图3）。

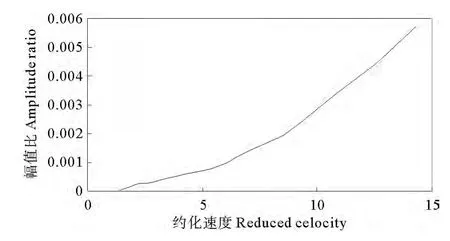
图3 顺流向涡激运动幅值比随约化速度的变化Fig.3 The relationship between in－line amplitude ratio of VIM and reduced velocity

从图中可以看到，顺流向的幅值比随着约化速度的增加而增加，是一个递增曲线，可见流速的大小对于平台顺流向的运动幅值起着关键的作用。但是顺流向的运动响应很小，即使在约化速度为15的情况下，其幅值比仅约为0.006，即位移为0.168m。所以目前对于Spar平台的顺流向响应基本不予以考虑。

图4是1m／s流速时顺流向涡激运动位移响应情况，可见Spar平台在顺流向产生了恒定的刚体位移23.78m，并在这个位置附近来回振荡。

运用Matlab对数据采用快速傅里叶变换（FFT）进行谱分析，得位移周期见图5，清晰可见与涡激升力一致的运动周期56s。通过图5可知，连接段处涡旋脱落对平台整体顺流向的运动响应影响比较微弱，因为通过计算可知连接段处涡旋脱落所引起的顺流向振动周期为28s，而这个数据在周期图上并不是很明显。

图4 1m／s时平台顺流向位移图Fig.4 Displacement time history in the in－line direction when the velocity is 1m／s

图5 1m／s时的周期图Fig.5 Periodogram when the velocity is 1m／s

3.2 考虑非线性阻尼时横流向涡激运动响应

平台的横流向涡激运动是指涡旋脱落时对平台引起垂直于来流方向的升力，导致平台产生垂直于来流方向的往复运动，相关圆柱形平台的运动方程如下：

式中：CL为升力系数，与Re有关；y为立管横流向振动位移；ly为立管横流向振动速度为立管横流向振动即为非线性阻尼项。

运用Matlab对平台的运动方程进行编程计算，分析Spar平台考虑流固耦合时在流速0.2～2m／s工况中，由于涡泄引起的横流向振动响应（见图6）。

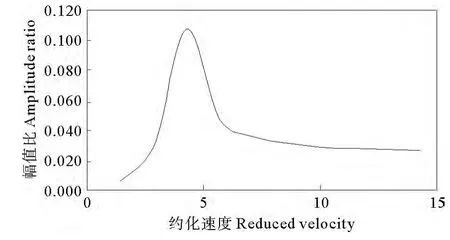
图6 横流向涡激运动幅值比随约化速度的变化Fig.6 The relationship between crosss－flow amplitude ratio of VIM and reduced velocity

从图中可以看到，随着约化速度的增加，横流向的幅值比先增加后减小，在约化速度为5的附近出现一个峰值，此时硬舱涡泄引起的横流向升力频率接近平台的固有频率，结构发生共振。从图形可见，这与顺流向的运动响应有一定的不同，制约横流向运动响应幅值的不再是单一的流速，而是与结构的固有频率也有一定的关系，来流引起的升力频率越远离固有频率，响应则越小。同时又可从图中看到，横流向的响应幅值比明显比顺流向的大得多，在共振时，平台的幅值比达到了0.11附近，即位移为3.08m，这使得横流向涡激运动的研究成为Spar平台两向涡激运动的重点。

图7是1m／s流速时横流向涡激运动位移响应情况，可见Spar平台在位移为0处来回振荡，做简谐运动，幅值接近1m。

图7 1m／s时平台横流向位移图Fig.7 Displacement time history in the cross－flow direction when the velocity is 1m／s

运用Matlab对数据采用快速傅里叶变换（FFT）进行谱分析，得位移周期图8，清晰可见与涡激升力一致的运动周期56，112s和平台的固有周期200s。其中周期56s是连接段涡激升力产生的，周期112s是硬舱和软舱涡激升力产生的。从图8可见，涡激升力周期与平台固有周期比较接近，随着流速的降低，平台将会和涡激产生的升力产生共振，这和图6显示的结果一致。

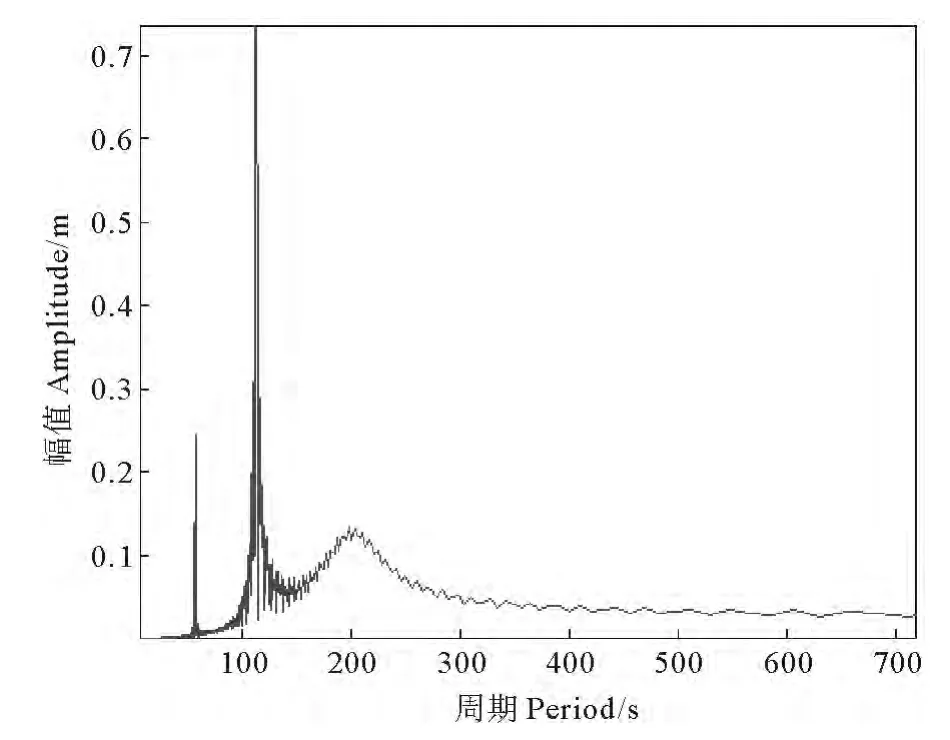
图8 1m／s时的周期图Fig.8 Periodogram when the velocity is 1m／s

3.3 非线性阻尼对顺流向涡激运动响应的影响

为了进一步了解流固耦合中非线性阻尼力对结构运动的影响，不考虑非线性阻尼力时的结构运动模型同样通过Matlab建立起来，这里先讨论非线性阻尼力对顺流向涡激运动响应的影响。

Spar平台在海流作用下产生涡激运动，顺流向的运动较横流向的运动幅度小得多。通过Newmark－β法同样建立不考虑非线性阻尼时的顺流向模型，方程如下，可与公式（9）进行对比：

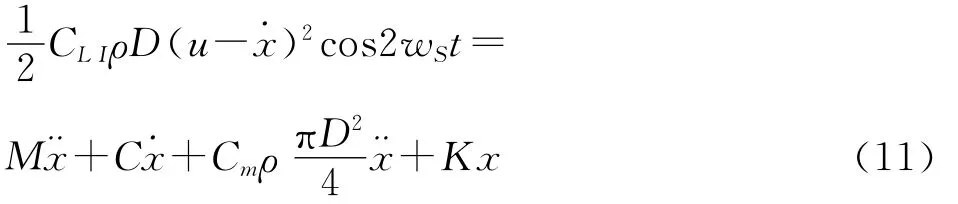
运用方程（11）计算得平台此时的运动响应，同样平台的位移以幅值比的形式给出。为了方便比较，同时将考虑非线性阻尼时，平台顺流向的响应情况在图中给出（见图9）。

图9 顺流向涡激运动幅值比随约化速度的变化Fig.9 The relationship between in－line amplitude ratio of VIM and reduced velocity

通过上图比较发现平台考虑非线性阻尼时的顺流向响应比不考虑时来得小，而且响应均随着约化速度的增加而增加，在约化速度为2.5附近都有一定的突变增加，这是由于在这个约化速度时，平台上部硬舱的顺流向涡激升力频率与平台固有频率接近。然而在共振时，显然非线性阻尼的作用更为明显，它能有效的降低平台顺流向共振时位移响应的计算结果，这对于Spar平台将来可能的顺流向位移计算有一定的参考价值。

3.4 非线性阻尼对横流向涡激运动响应的影响

Spar平台涡激运动时横流向的响应是目前研究热点，是Spar平台设计的重要指标。平台涡激运动时横流向运动的幅值较顺流向运动的幅值大得多，对结构和系泊系统的影响更为显著。对于Spar平台涡激运动的横流向响应必须控制在一定范围内。

通过Matlab软件对Spar平台不考虑非线性阻尼时的情况进行编程，方程如（12），可与公式（10）进行比较。

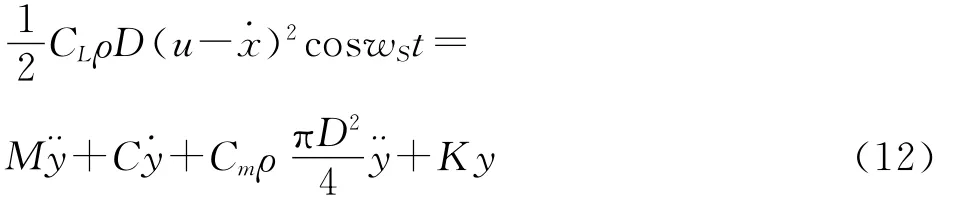
将不考虑非线性阻尼时的横流向响应数据同样以幅值比的形式给出，同时引入考虑非线性阻尼时的数值模拟结果进行比较（见图10）。

图10 横流向涡激运动幅值比随约化速度的变化Fig.10 The relationship between crosss－flow amplitude ratio of VIM and reduced velocity

通过上图比较发现平台考虑非线性阻尼时的横流向响应比不考虑时的响应来得小，这与顺流向的比较情况是一致的，然而横流向响应随着约化速度的增加先增加后减小，在约化速度为5附近出现峰值，这是由于在这个约化速度时，平台上部硬舱的横流向涡激升力频率与平台固有频率接近。在共振时，显然非线性阻尼的作用也是更为明显，它能有效的降低平台横流向共振时位移响应的计算结果。在峰值两边，两条曲线基本重合，可见，当平台不发生共振时，非线性阻尼的作用对于平台的横流向运动响应的计算结果影响很小，这对于Spar平台横流向位移计算有一定的参考价值。

3.5 模型数值验证

为了验证本文数值模拟结果的正确性，本文将考虑非线性阻尼的横流向数值模拟结果与文献［6］进行了对比（见图11）。

图11 数值模拟对比图Fig.11 Comparison diagram of numerical simulation

从图中可以看出，本文计算结果和文献［6］有着一定的吻合性，在约化速度4～6区间内，幅值比均有明显上升趋势，由于本文考虑了非线性阻尼的影响，而且本身Spar平台的结构阻尼较文献［6］中的结构阻尼大，因此在锁定区本文的横流向幅值比比文献［6］中的小是合理的。在约化速度小于4或者大于6时，本文的计算数据与文献［6］有着明显的一致性，这很好的验证了本文理论数值计算的正确性。

4 结论

通过对Spar平台两向涡激运动的数值模拟，得到以下结果：

（1）得到了Spar平台考虑流固耦合时两向涡激运动位移响应情况，并通过频谱分析得到了相应的周期图。其中横流向周期图能较好地反映出硬舱和连接段2个不同直径处的涡泄周期，同时还能从图中观察到平台的固有周期。

（2）顺流向涡激运动响应随着约化速度的增大而增大。横流向涡激运动响应随着约化速度的增大先增大后减小，图形曲线与顺流向的完全不同，在约化速度5附近出现峰值，此时发生共振，由于其幅值较顺流向的大得多，因此横流向运动成为Spar平台涡激运动考虑的重点。

（3）计算非线性阻尼对Spar平台两向涡激运动影响时发现，非线性阻尼能降低Spar平台两向涡激运动的计算结果，并且在共振时，减小的幅度更大。可见在Spar平台两向涡激运动的计算中，只有在远离共振的情况下才可以忽略非线性阻尼。

（4）为了方便计算，本文忽略了涡泄引起的平台的横摇和纵摇问题，有待日后继续深入研究。

［1］ 葛斐，龙旭，王雷，等.大长细比圆柱体顺流向与横向耦合涡激振动的研究 ［J］.中国科学，2009，39（5）：752－759.

［2］ 张立武，陈伟民.深水细长柔性立管涡激振动响应形式判定参数研究 ［J］.中国海上油气，2010，22（3）：202－206.

［3］ 王颖，杨建明，李欣，等.均匀来流中浮式圆柱的涡激运动研究［J］.中国海洋平台，2010，25（1）：8－15.

［4］ 王颖，杨建民，杨晨俊.Spar平台涡激运动关键特性研究进展［J］.中国海洋平台，2008，23（3）：1－10.

［5］ 高云，宗智，于馨.Spar平台涡激运动响应分析 ［J］.中国海洋平台，2011，26（1）：17－22.

［6］ 高云，宗智，于馨.均匀来流中Spar平台涡激运动响应研究 ［J］.中国科学，2011，41（2）：132－139.

［7］ 张蕙，杨建民，肖龙飞，等.均匀流中深水系泊Truss Spar平台涡激运动试验研究 ［J］.海洋工程，2011，29（4）：14－20.

［8］ Sampath Atluri，John Halkyard，Senu Sirnivas.CFD simulation of truss spar vortex－induced motion ［C］.∥ Hamburg，Germany：The 25th International Conference on Offshore Mechanics and Arctic Engineering，2006.

［9］ Dominique Roddier，Tim Finnigan，Stergios Liapis.Influence of the reynolds number on spar vortex induced motions（VIM）：multiple scale model test comparisons［C］.∥Honolulu，Hawaii：Proceedings of the ASME 28th International Conference on Ocean，Offshore and Arctic Engineering，2009.

［10］ Wang Ying，Yang Jianmin，Lv Haining.Computational fluid dynamics and experimental study of lock－in phenomenon in vortexinduced motions of a cell－truss spar［J］.Journal of Shanghai Jiaotong University（Science），2009，14（6）：757－762.

［11］ 孟韬.基于 MATLAB的Newmark－β动力反应数值分析法的精度稳定性分析 ［J］.金色年华，2010，7（6）：6.