不对称独塔斜拉桥风致颤振分析
2014-10-13汪荣绣张景君
汪荣绣,张景君
(大连理工大学建设工程学部,辽宁 大连 116024)
斜拉桥是一种由主梁、索塔和斜拉索3部分组成的高次超静定组合的典型柔性结构,在风荷载作用下容易发生变形和振动,因此对此类桥梁进行抗风性能分析非常重要。其中颤振失稳是最显著的问题。颤振是指在平均风作用下,作为空间结构的桥梁系统,从流动的空气中不断吸收大于结构阻尼耗散能力的发散性气动力引起的自激振动。桥梁颤振的主要形式有古典耦合颤振和分离流扭转颤振,是桥梁结构风致振动中最危险的振动形式[1]。
1 工程概况
盘锦某斜拉桥设计方案为天鹅造型的单塔空间索面斜拉桥,跨径布置为(79.5+185)m。斜拉桥采用塔梁固结、塔墩分离体系,主梁和索塔均采用钢结构。斜拉桥主梁采用钢箱梁,其中主跨主梁为带风嘴的单箱三室钢箱梁;边跨主梁为边主梁形式,由两边的边箱和中间箱梁组成。索塔为空间结构,外形如天鹅的头和颈。索塔顺向弯折,下部两塔柱向边跨倾斜约16.2°,同时向桥中线内倾斜11.9°。斜拉索采用镀锌高强平行钢丝索,钢丝强度为1 670 MPa,钢丝束外设PE护套,两端采用冷铸锚。主跨共13对斜拉索,共26根。边跨背索分为2组,每组4根,共计8根。桥梁结构如图1~3所示(图1~3中长度单位为cm)。
柔性斜拉桥对风的作用比较敏感,因此在设计阶段进行风颤分析非常有意义。由于本桥采用支架施工,施工阶段的抗风性能可以不予考虑,主要研究成桥运营阶段的风致颤振[2-3]。
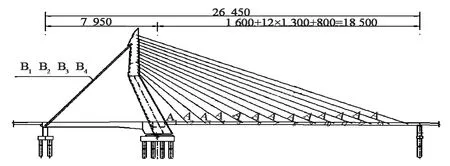
图1 桥梁立面图
2 结构动力特性计算
2.1 建立有限元模型
斜拉桥动力特性分析是桥梁结构进行抗风分析的基础,计算模型的选取直接影响结构的动力特性。模型应注重结构刚度、质量及边界条件的模拟,尽量与实桥相符。
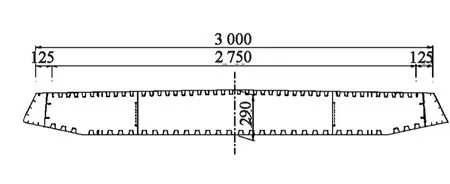
图2 主跨钢箱梁断面图
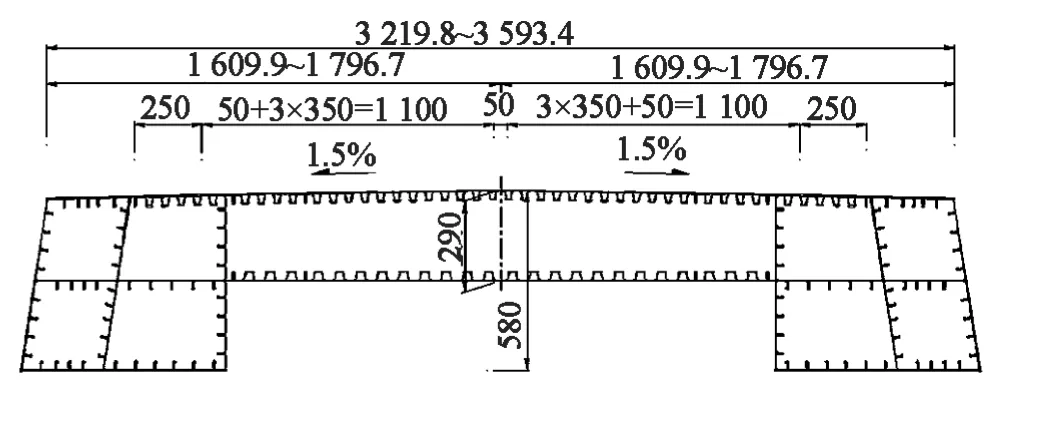
图3 边跨钢箱梁断面图
1)单元划分及模拟
计算模型采用Midas Civil有限元分析程序建立空间三维模型,单元类型的选择和单元尺寸的划分是有限元分析首先要解决的问题。将斜拉索定义为索单元,索塔和主梁定义为梁单元。主梁和索塔根据结构本身的特点按合适的间距进行单元划分,关键截面的单元划分较密,边跨主梁和索塔是变截面,单元划分较密。单元截面采用截面特性计算器进行计算。主梁为封闭箱型,采用单脊梁式模型,桥面系的刚度和质量都集中在中间节点上。主跨和边跨横梁、风嘴结构以及二期恒荷载以梁单元荷载通过静力工况施加,在进行特征值分析过程中将结构自重和荷载转化为质量。承台近似按刚体模拟,质量堆聚在承台质心。对于群桩基础采用六弹簧模型模拟[4-5]。
2)边界条件的处理
本桥分析中未包括非线性时程分析的内容,所以边跨主跨支座用一般支承来模拟,只约束竖向位移。由于该桥为空间索面斜拉桥,所以吊点和主梁间采用刚性连接,使主梁重量通过斜拉索传递至索塔上。梁塔连接模拟为钢臂单元。
3)荷载及支座沉降分析
成桥状态下,斜拉索以初拉力形式施加,考虑结构体系的升降温及斜拉索的升降温作用。考虑支座的不均匀沉降,主跨和边跨支座沉降1 cm,中墩沉降1 cm。
斜拉桥结构Midas计算模型如图4所示。
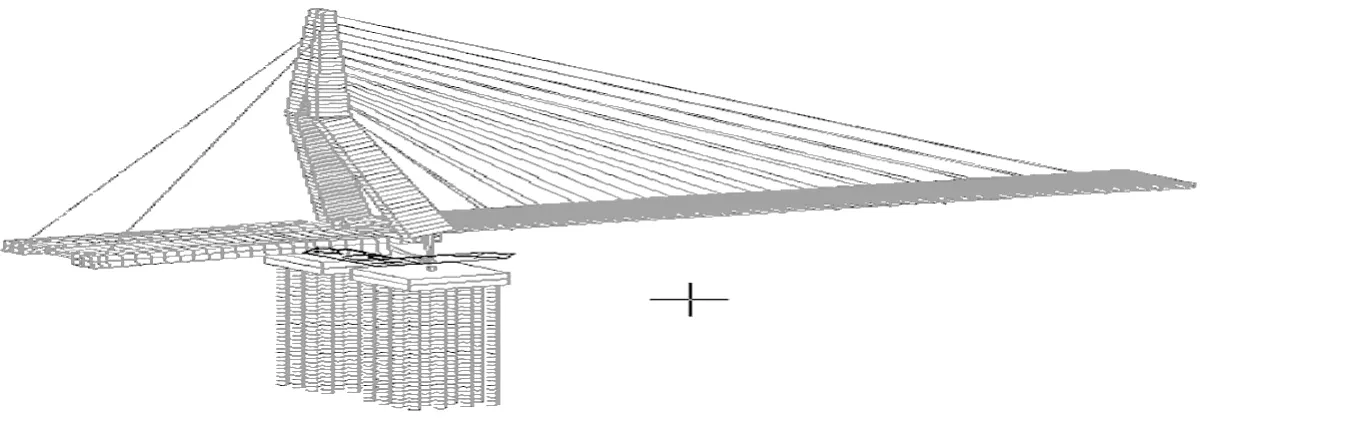
图4 Midas有限元计算模型
2.2 自振频率及振型
结构动力特性计算主要包括自振频率计算及振型分析。在模型中首先将自质量转换为x、y、z 3个方向的质量,其次将二期荷载转换成质量,采用Lanczos方法进行特征值分析,得到全桥的多阶模态的频率及振型特征,如表1所示。桥梁主跨竖弯和扭转的振型图,如图5、6所示。
由表1及图5、6可知,该斜拉桥的结构振动特性为:1)本桥第二振型是主梁的一阶对称竖弯,自振周期为1.346 s,自振周期比较短,自振特性与传统的柔性斜拉桥显著不同,这种桥梁的抗风性能较好。2)对于斜拉桥,斜拉索的作用使侧向弯曲和扭转强烈耦合在一起,其结果不是单纯的扭转振型,这使得颤振形态变得复杂。3)该桥采用的是双索面、钢箱梁截面,提高了结构的抗扭刚度,扭转频率相对较高。4)从振型可以看出,由于结构的不对称性,结构的自振特性表现出明显的不完全对称,塔、梁、墩、索的振动互相影响[6-12]。
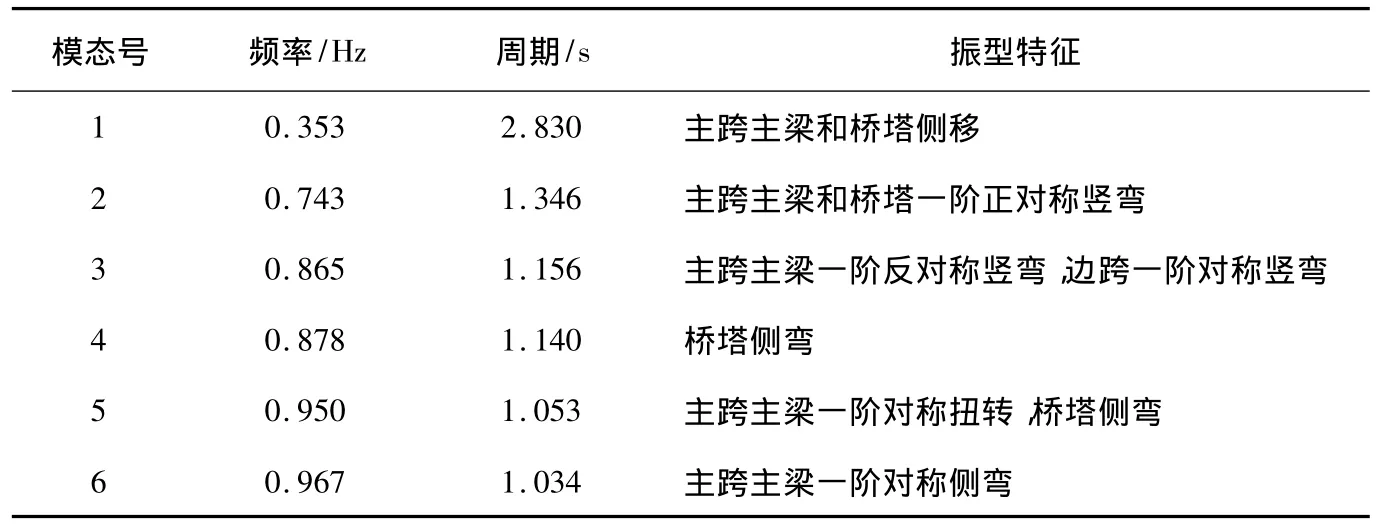
表1 盘锦某斜拉桥前6阶模态的频率值及振型特征

图5 结构一阶对称竖弯模态(f=0.743 Hz)

图6 结构一阶对称扭转模态(f=0.950 Hz)
3 颤振分析
3.1 颤振检验风速
大桥处于辽宁省盘锦市,根据文献[13],地表粗糙度为B类,桥址处的基本风速v10=31.3 m/s,设计基准风速vd的计算式为
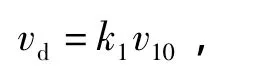
式中 k1为风速高度变化修正系数,k1=1.1。
可得 vd=35.1 m/s。
颤振检验风速计算式为
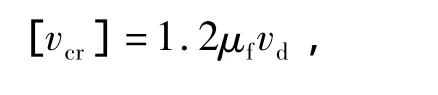
式中 μf为风速脉动修正系数,μf=1.32。
计算得[vcr]=55.6 m/s。
3.2 弯扭耦合颤振
桥梁的弯扭耦合颤振临界风速vcol采用Van der Put公式计算[13],计算式为
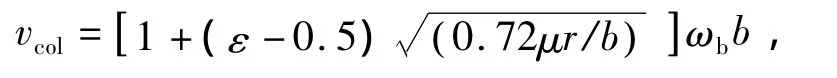
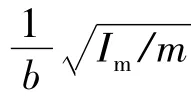
3.3 分离流扭转颤振
桥梁的分离流扭转颤振临界风速vco2由Herzog公式计算[14],计算式为
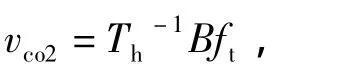
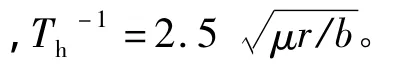
可得vco2=230 m/s>[vcr],对于成桥状态,在当地最大风速作用下不会发生纯扭颤振失稳。
由成桥状态验算结果可知,纯扭转颤振临界风速达230 m/s,远远大于颤振临界检验风速;弯扭耦合颤振临界风速也大于颤振检验风速,能够通过抗风稳定性检算,可以不必进行风洞试验[15]。
4 结语
以盘锦某不对称独塔斜拉桥为例,对该桥成桥状态进行动力特性分析,并在此基础上进行抗风稳定性验算。分析结果表明,纯扭颤振临界风速和弯扭耦合颤振临界风速均大于主梁自激风振的检验风速,因此本桥成桥运营状态能有效防止发散的自激风振。
[1]陈政清,项海帆.桥梁风工程[M].北京:人民交通出版社,2005.
[2]顾安邦,范立础.桥梁工程[M].北京:人民交通出版社,2000.
[3]项海帆.公路桥梁抗风设计指南[M].北京:人民交通出版社,1996.
[4]邱顺东.桥梁工程软件 midas civil应用工程实例[M].北京:人民交通出版社,2011.
[5]邱顺东.桥梁工程软件 midas civil常见问题解析[M].北京:人民交通出版社,2011.
[6]黎曦,涂忠仁,顾安邦.彭溪河特大斜拉桥风致颤振分析[J].重庆交通大学学报,2007,26(6):29-33.
[7]郑斐,黄江,范骏.部分斜拉桥结构分析[J].山东交通学院学报,2007,15(3):37 -42.
[8]杨军,邱文亮.独塔自锚式悬索桥动力特性分析[J].山东交通学院学报,2009,17(1):40-43.
[9]李春才.钢架拱桥动力分析与试验研究[J].山东交通学院学报,2010,18(3):36-41.
[10]谭明伦,段爱忠.钢箱梁独塔斜拉桥抗风性能研究[J].公路交通科技,2013(7):250-253.
[11]田晓霞,陈才俊.斜拉桥抗风性能分析方法及其对策[J].建筑与工程,2011(19):718-719.
[12]蒋华,韦陶贤.矮塔斜拉桥结构动力特性分析[J].四川建材,2011,37(6):100 -102.
[13]中交公路规划设计院.JTG/T D60-01—2004 公路桥梁抗风设计规范[S].武汉:武汉理工大学出版社,2004.
[14]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1992.
[15]项海帆.现代桥梁抗风理论与实践[M].北京:人民交通出版社,2005.
