小方坯连铸结晶器内热力行为研究

符 豪 张炯明 赵新凯 肖 超

(北京科技大学)

0 引言

钢铁生产已经从模铸时代步入到连铸时代，连铸生产以其效率高、产品质量好及生产灵活性高而著称。为了最大限度地了解连铸过程及连铸机理，尤其是结晶器内部的热力状况，工业试验是必不可少的。然而由于工业试验需要花费大量的时间和金钱，而对于某些试验在现在的生产条件下还不能完成。计算机模拟技术成本低，可重复性强，模拟结果直观方便，因此计算机模拟技术成为了了解连铸过程的很好选择。1967年，E.A.Mizikar首次使用了一维差分有限元模型，用于计算铸坯温度场以及坯壳厚度［1］，这一模型预测了冶金长度、坯壳厚度以及拉速之间的关系。此后，工业试验对此模型进行了验证［2］。Brimacombe首次提出要把模拟计算与工业试验相结合，这一思想的提出，指导了未来连铸模拟技术发展的方向［3-4］。1982年，二维模型首次由Samarasekera和Brimacombe应用，从此模拟技术进入二维时代［5］。在结晶器内坯壳凝固过程中，不仅发生传热，也会有各种应力应变的作用，Grill、Weinberg等，首次考虑了坯壳凝固过程中的应力应变作用［6-7］。前人的 努力为以后连铸过程中数值模拟技术打下了坚实的基础。最近，国外的Chun Sheng Li［8］及 Rajil SARASWAT［9］等，应用连铸热力耦合模型对坯壳裂纹、结晶器锥度等问题进行了研究。国内东北大学的蔡兆镇［10］，大连理工大学的李婧［11］，Wang Tongmin［12］也应用此模型进行了一系列研究。但以上模型均为二维有限元模型，二维模型的特点是忽略了拉坯方向的传热，改变实际的三维传热为更加简单的二维传热，而对于二维模型和三维模型的真正的区别，却很少有文献研究。笔者通过建立更符合实际的三维有限元模型，考虑了由于坯壳凝固收缩产生的气隙对传热的影响，研究了结晶器铜板温度及坯壳温度分布状况;拉速和过热度对于热流密度的影响;模型计算了坯壳和铜板之间的气隙分布，特别关注了气隙在横向的分布，研究结果表明坯壳气隙在横向上差别很大，进而提出了结晶器横向锥度的概念，对结晶器设计有一定的指导意义。

1 模型描述

通过建立一个三维的热力耦合模型(使用商业软件Thercast)，来揭示方坯连铸内部温度、应力应变等的变化过程。这一模型的显著特征是各个区域相互独立，分别可以对结晶器、保护渣、钢液等独立划分网格，设置相应参数，在本次模拟中，结晶器和保护渣只进行热计算，钢液及凝固坯壳进行热力计算。模型如图1所示，因为方坯的对称性，此模型为1/4控制模型，为了在保证计算精度的前提下，提高计算速度，坯壳和结晶器接触位置，采用细网格，钢液中心采用粗网格。

图1 模型俯视图

国内某钢厂连铸结晶器参数见表1。在本次模拟中，忽略了方坯结晶器的弧度，把结晶器当作直结晶器进行处理。模拟钢种为40Cr，其物性参数见表2。

表1 连铸结晶器参数

表2 40Cr物性参数

1.1 方坯内部传热控制方程

方坯内部传热方程如下式：

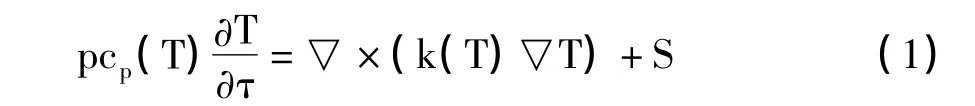
式中：ρ——金属密度，kg/m3;

cp(T)——与温度有关的热熔，J/(kg·℃);

S——为源项，W;

k(T)——与温度有关的导热系数，W/(m·k)。

在钢液内部，由于钢液的流动，已经不是单一的传导传热，一般通过人为扩大导热系数的方法对k处理［13］。

式中：TL——钢液液相线温度，K;

T——钢液温度，℃;

K——等效导热系数，W/(m·k);

m——为常数(一般为4～8，在本次模拟中取6)。

k*——钢液的导热系数，W/(m·k);

关于凝固潜热，通过源项进行考虑。

1.2 方坯/结晶器界面传热控制

把传热热阻和电阻进行类比，可以得出冷却水和坯壳之间传热如图2所示。

图2 冷却水和坯壳之间传热

冷却水和铜板之间的传热热阻可由下式表示：

式中：Rwater——冷却水与铜板之间的传热热阻，k/(m2·w);

hw——冷却水与铜板之间换热系数，(m2·w)/k。

式中：D——等效铜管直径，m;

f——冷却水的流通截面积，m2;

U——湿周，m;

uw——冷却水的平均流速，m/s;

μw——冷却水的粘度，Pa·s;

ρw——冷却水的密度，kg/m3;

λw——冷却水的导热系数，W/(m·k);

cpw——冷却水的比热容，J/(kg·k)。

铜板热阻(Rcopper)由铜板厚度和铜板导热系数控制，可由下式表示：

式中：dcopper——铜板厚度，m;

λcopper——铜板导热系数，W/(m·k)。

铜板和保护渣之间的接触热阻(Rcontact)，由铜板和保护渣性质决定。Rslag为保护渣热阻，由保护渣厚度和保护渣导热热阻控制(在本次模拟中，对实际情况进行了简化处理，保护渣厚度设置为一定值)。

式中：dslag——保护渣厚度，m;

λslag——保护渣导热系数，W/(m·k)。

热量通过气隙有两种方式，传导传热和辐射传热，因此，气隙热阻(Rair)可由下式得出：

式中：hair——总的气隙换热系数，W/(m2·s);

hcond——传导换热系数，W/(m2·s);

hrad——辐射换热系数，W/(m2·s);

Kair——气隙导热系数，W/(m·k);

dair——气隙大小，m;

σr——波尔兹曼常数;

T1和ε1——分别为物体1的温度和辐射系数;

T2和ε2——分别为物体2的温度和辐射系数。

1.3 边界条件

在本次模拟中，铜板四周设置对流传热的边界条件，对流换热系数可以根据连铸的实际状况进行计算(公式(4))。由于冷却水温度变化不大，冷却水设定为恒温状况。

1.4 应力模型

钢液在凝固过程中，凝固坯壳经历了复杂的应力应变的作用：①由于重力的作用，坯壳会受到内部钢液的静压力的作用，②由于坯壳的凝固收缩，会产生一个收缩应力的作用，③由于结晶器锥度或者结晶器震动的原因，外部坯壳可能会受到铜板接触应力的作用。总的应变由以下三部分组成：

式中：εe——弹性应变;

εt——热应变;

εp——塑性应变。

2 模型验证

由于验证模型的工业试验非常复杂，需要花费大量的时间和资金。因此，本次模拟中采用Park所提供的连铸参数，与其通过实验测量的坯壳厚度及结晶器铜板温度进行比较来验证模型［14］。为测量的铸坯中心位置坯壳厚度与模拟计算结果的比较如图3所示，测量结果和模拟结果基本吻合。测量的铜板温度(铜板厚度中心温度)与模拟的铜板温度的对比如图4所示，模拟和实测铜板温度稍有差距，但基本吻合。

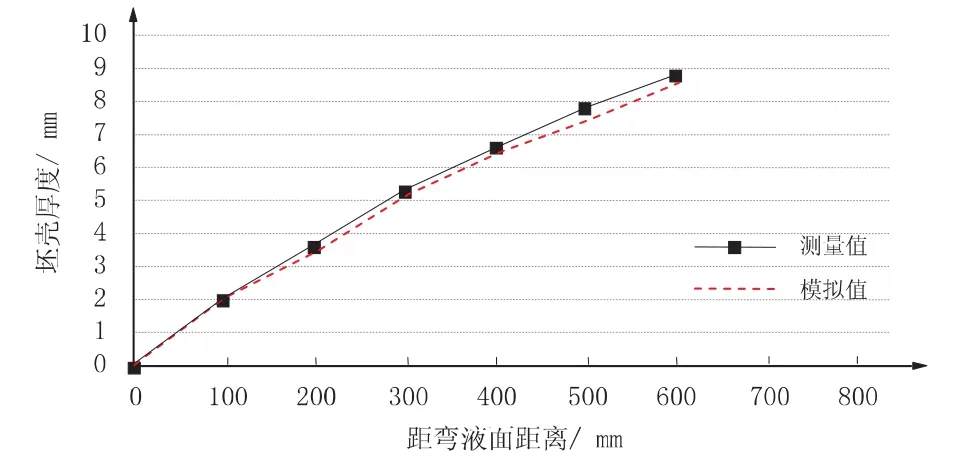
图3 测量坯壳厚度和模拟值对比

图4 测量铜板温度和模拟值对比

3 结果分析

3.1 铜板和坯壳温度场分布

根据表1及表2中的钢种参数及连铸参数，导入到THERCAST中计算。结晶器铜板中心冷热面温度分布如图5所示。

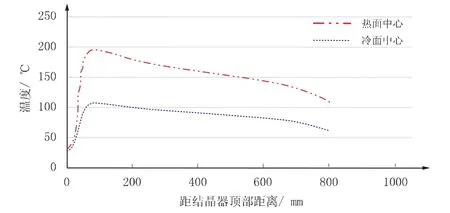
图5 结晶器铜板温度

由图5可以看出，在40 mm处为弯月面位置，在开浇阶段结晶器冷热面温度均直线上升，并在100 mm左右达到最高。冷面中心和热面中心温度在结晶器出口处呈现明显下降趋势，这与出口处中心部位的气隙有关，在这一位置，坯壳强度足以抵抗钢水静压力，因此会形成一定的气隙。

Joong Kil PARK［15］使用二维模型所得到的结果如图6所示。

图6 二维模型铜板温度

对比本次三维模型的结果可以看出，在三维模型中，在弯月面以上位置，铜板冷热面温度有了一些细微差别，在二维模型中，在弯月面以上铜板冷热面对比本次三维模型的结果可以看出，在三维模型中，在弯月面以上位置，铜板冷热面温度有了一些细微差别，在二维模型中，在弯月面以上铜板冷热面温度相同，这主要是因为三维模型考虑了拉坯方向上的传热，而二维模型不能考虑到在拉坯方向上的传热。

铸坯沿拉坯方向温度曲线(弯月面在40 mm处)如图7所示。

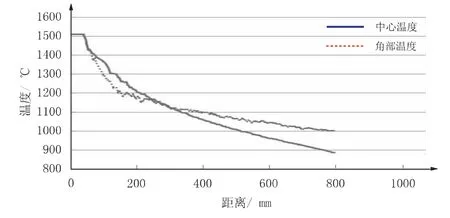
图7 沿着拉坯方向坯壳温度

由图7可以看出，坯壳温度在总体上呈下降趋势，但在局部有回温现象，出结晶器坯壳最低温度为900℃左右，最低温度在中心位置。在0～260 mm位置，角部温度低于中心温度，这是由于角部二维传热的原因，但随着角部气隙增大，热阻增大，角部温度逐渐高于中心温度，在出口处其角部最低温度为998℃。结晶器出口位置处坯壳横向位置温度分布云如图8所示。可以看出温度横向分布状况。

图8 结晶器出口处坯壳横截面温度分布

3.2 拉速和过热度对热流密度的影响

不同拉速下沿拉坯方向上热流密度的大小分布如图9所示。

图9 不同拉速下热流密度沿着拉坯方向分布

由图9可以看出，拉速增加，热流密度随着增加，但热流密度的增加与拉速的增加并不成线性关系，在拉速从0.025 m/s～0.032 m/s时热流密度的增加大于拉速从0.032 m/s～0.039 m/s时热流密度的增加，由此可知，拉速增加会在一定程度上增加热流密度，但增加的程度有限，且拉速很高时，通过提高拉速很难增加热流密度。拉速对热流密度的影响主要有三方面原因：①拉速增加，坯壳在结晶器中停留时间减少，从而导致坯壳厚度变薄，在钢水静压力的作用下，气隙会更小，从而使热流密度增加;②坯壳在结晶器中停留时间短，坯壳表面温度会增加，传热的温度梯度也会增加;③更薄和更高温度的坯壳，由于温度下降引起的收缩也会减少，坯壳和结晶器间间隙更小。

不同拉速下结晶器出口处坯壳应力分布云如图10所示。

图10 不同拉速下周向应力分布

由图10可以看出，不同拉速下，坯壳内部应力稍有差别，但差别不大。

不同过热度下热流密度沿拉坯方向分布如图11所示。

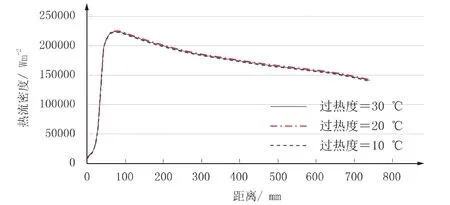
图11 不同过热度热流密度随着拉坯方向分布

由图11可以看出，过热度增加热流密度增加很小，几乎没有增加，对于此现象可以通过以下方程式解释：

式中：q——热流密度，W/(m2·s);

Tshell——坯壳表面温度，K;

Twater——冷却水温度，K;

R总——总的热阻(包括冷却水和铜板之间热阻，铜板内部热阻，铜板和保护渣之间接触热阻，保护渣内部热阻及保护渣和坯壳之间热阻)，(m2·K)/W。

浇注温度改变，对坯壳表面温度影响很小，因此热流密度变化不明显。不同过热度下坯壳在结晶器出口处厚度如图12所示。

图12 不同过热度下坯壳厚度

由图12可以看出，过热度越大，坯壳厚度越薄，但趋势不是太明显，这主要因为由于过热引起的总的热量的增加与凝固潜热相比很小。

3.3 气隙结果及对结晶器设计的指导

坯壳表面气隙分布轮廓如图13所示，为中心和角部气隙大小沿纵向分布曲线如图14所示。

图13 气隙分布轮廓图

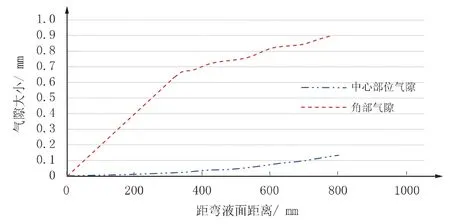
图14 中心和角部气隙大小沿纵向分布

由图13、图14可以看出，坯壳角部气隙在弯月面以下位置开始形成，在0～400 mm气隙增长很快，在400 mm～800 mm气隙缓慢增长，这主要与角部传热有关，在初始阶段热阻较小，热流大，坯壳厚度增长快，因此形成的凝固收缩也大。中心气隙在0～300 mm位置基本为0，这是因为坯壳强度低，不能承受钢水静压力的作用，在300 mm～800 mm位置，气隙开始形成，并缓慢增加。

提高拉坯速度是提高连铸生产效率的首要方法，限制拉坯速度主要是出结晶器坯壳厚度。降低浇注温度和增加结晶器长度在一定程度上能提高出结晶器坯壳厚度，但是浇注温度过低会早成凝钢的危险，同时也会影响夹杂物的上浮，结晶器长度过长也会造成拉坯阻力增加，造成结晶器磨损，严重影响结晶器寿命。因此，提高结晶器与坯壳间传热，增加热流密度，从而提高出结晶器坯壳厚度是提高拉速的关键。从温度场分布以及气隙分布可以看出，坯壳角部由于气隙的存在，热流密度很小，坯壳温度高，结晶器出口处坯壳厚度薄。由于角部坯壳厚度薄、温度高，从而强度较低，是形成角部裂纹和漏钢的主要原因，因此限制了坯壳拉速的提高。目前，结晶器多为多锥度或者连续锥度，在横向分布上几乎没有区别。不同拉坯位置气隙沿横向分布曲线如图15所示。

图15 气隙大小横向分布

由图15可以看出，如果结晶器锥度设计以中心凝固收缩为标准，就会在角部形成气隙，限制了角部传热，造成角部温度局部过热，因此角部多形成裂纹和漏钢;如果铜板锥度设计以角部凝固收缩为标准，就会造成其它位置锥度过大问题，使其与铜板挤压，增大拉坯阻力，造成铜板磨碎严重，有时甚至会拉断坯壳。对于这种情况，国外的Martellucci等也进行了研究，并发明了一种新型结晶器(如图16所示)［16］。这种结晶器在入口处四角向外凸，随着拉坯方向逐渐向里收缩，在出口处重新恢复方形。角部的收缩极大地减小了导热热阻，提高了热流密度，因此提高了出结晶器坯壳厚度，拉速由此可以提高。但这种结晶器主要考虑了角部气隙的影响，对于非角部区域的锥度并没有考虑，因此，这种结晶器也有待改进。可以看出，结晶器锥度设计应充分考虑纵向锥度和横向锥度，只有这样才能尽可能的减小气隙，增加热流密度，提高拉速和铸坯质量。根据这种设计思路，重新设计了的结晶器(如图17所示)。

图16 国外设计结晶器

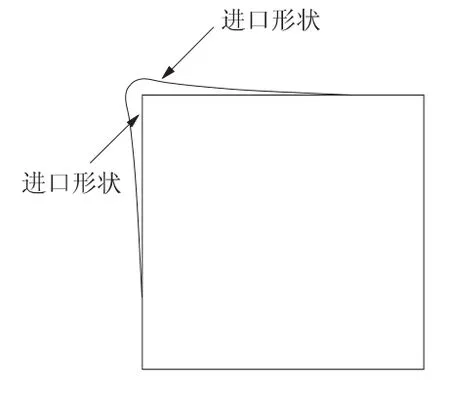
图17 新设计的结晶器

5 结论

1)采用三维有限元计算模型，研究了结晶器铜板及坯壳温度场分布，并对比了三维模型和二维模型铜板分布的差异。引起三维模型和二维模型铜板温度场差异的主要原因是二维模型忽略了拉坯方向的传热，三维模型则能考虑这一方向的传热。坯壳横向温度分布不均衡，在距弯月面0～260 mm处，角部温度低于中心温度，在大于260 mm至弯月面处，中心温度低于角部温度。

2)研究了拉速及过热度与热流密度的关系，在拉速增高的情况下，热流密度增大，分析了热流密度增加的原因，但在拉速达到一定程度时，增加拉速基本不能增加热流密度。过热度增加，热流密度增加量很小，解释了过热度对热流密度影响较小的原因。但过热度的大小对出结晶器坯壳厚度有一定影响。

3)结晶器锥度设计是提高拉坯速度和铸坯质量的关键，以往的结晶器锥度仅仅考虑了结晶器纵向锥度设计，而对于横向锥度的考虑却很少。通过本次模拟，研究了结晶器横向气隙分布，对结晶器设计提供了参考。

［1］ Mizikar E A.Mathematical heat transfer model for solidification of continuously cast steel slabs［J］.AIME MET SOC TRANS，1967，239(11)：1747-1758.

［2］ R.Davies，N.Blake，and P.Campbell：4th Int.Conf.Continuous Casting，Preprints，Vol.2，Brussels，Belgium，17-19 May，1988，VS，Dusseldorf，FRG，1988，vol.2，pp.645-54.

［3］ Brimacombe J K.Design of continuous casting machines based on a heat-flow analysis：state-of-the-art review［J］.Canadian Metallurgical Quarterly，1976，15(2)：163-175.

［4］ Thomas B G，Moitra A，McDavid R.Simulation of Longitudinal Off-Corner Depressions in Continuously-Cast Steel Slabs［J］.Urbana，1996，51：61801.

［5］ Samarasekera I V，Brimacombe J K.Proc.3rd PTD Conf.on Application of Mathematical and Physical Models in the Iron and Steelmaking Industry［J］.1982，9(1)：1-15.

［6］ Grill A，Brimacombe J K，Weinberg F.Mathematical analysis of stresses in continuous casting of steel［J］.Ironmaking Steelmaking，1976，3(1)：38-47.

［7］ Brimacombe J K，Sorimachi K.Crack formation in the continuous casting of steel［J］.Metallurgical transactions B，1977，8(2)：489-505.

［8］ Li C，Thomas B G.Ideal taper prediction for billet casting［C］//ISSTECHCONFERENCEPROCEEDINGS.IRONANDSTEEL SOCIETY，2003：685-700.

［9］ Saraswat R，Maijer D M，Lee P D，et al.The effect of mould flux properties on thermo-mechanical behaviour during billet continuous casting［J］.ISIJ international，2007，47(1)：95-104.

［10］ 蔡兆镇，朱苗勇.板坯连铸结晶器内钢凝固过程热行为研究I.数学模型［J］.金属学报，2011，47(6)：671-677.

［11］ 蔡兆镇，朱苗勇.板坯连铸结晶器内钢凝固过程热行为研究Ⅱ.模型验证与结果分析［J］.金属学报，2011，47(6)：678-687.

［12］ Tongmin W，Shaowu C，Jun L，et al.Mould taper optimization for continuous casting steels by numerical simulation［J］.Research ＆ Development，2010：61-66.

［13］ 陈家祥.连续铸钢手册［M］.北京：冶金工业出版社，1991：60-61.

［14］ Park J K，Thomas B G，Samarasekera I V.Analysis of thermomechanical behaviour in billet casting with different mould corner radii［J］.Ironmaking ＆ steelmaking，2002，29(5)：359-375.

［15］ Park J K，Li C，Thomas B G，et al.Analysis of thermo-mechanical behavior in billet casting［C］//ELECTRIC FURNACE CONFERENCE.2002，60：669-686.

［16］ Martellucci G.Continuous casting mold：European Patent EP 0931608［P］.2002-11-13.