反复荷载下水泥乳化沥青砂浆力学性能试验

徐 浩，王 平，徐井芒，曾晓辉

（1.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；2.西南交通大学 土木工程学院，四川 成都 610031）

水泥乳化沥青砂浆（CA 砂浆）充填层是板式无砟轨道结构的关键层之一，起着支撑、调整、传力、减振和隔振等作用［1－4］.关于CA 砂浆的力学性能及其主要影响因素已有学者进行了研究，谢友均等［4－6］研究了加载速率对CA 砂浆抗压强度的影响，发现CA砂浆抗压强度随加载速率的增大而增大.王涛等［7－8］对影响CA 砂浆强度的因素及其作用机理进行了分析，认为影响CA 砂浆强度的因素依次为水泥、乳化沥青和砂的用量，而且CA 砂浆强度主要由水泥决定，其弹性则主要由乳化沥青决定.此外有研究表明由于水的软化作用，无论采用低湿干燥法还是恒湿干燥法来调节硬化CA 砂浆的饱水度，CA 砂浆抗压强度及弹性模量均随其饱水度的增加而降低［9］.Wang等［10］则认为CA 砂浆的力学性能对温度较为敏感，其抗压强度和抗折强度均随温度降低而增大，而且沥青掺量越高，对温度越敏感.

在板式无砟轨道结构中，CA 砂浆充填层承受列车的反复荷载作用.研究CA 砂浆在轴压荷载下的反复荷载应力－应变曲线及其变形性能，对了解CA 砂浆的基本力学性能及其在板式无砟轨道中的适应性能以及分析板式无砟轨道结构在列车反复荷载作用下的强度和变形恢复能力是非常必要的.本文通过等应变增量的反复荷载试验，测定了现场取样CA 砂浆试件反复荷载应力－应变曲线，分析其在反复荷载下的弹塑性变形规律，并给出了反复荷载应力－应变曲线方程.

1 试件制作及试验过程

1.1 试件制作

为了反映实际运营中的CRTSⅠ型板式无砟轨道CA 砂浆的力学性能，试验所用CA 砂浆试件为施工现场取样，并加工成φ50×50mm 的圆柱体试件.现场取样CA 砂浆试件的原材料均来自安徽中铁工程材料科技有限公司，其干料24h体积膨胀率为2.1%，7d 线膨胀率为0.1%，1d 抗压强度为6.89 MPa；改 性 阳 离子乳化沥青固含量1）文中涉及的固含量、配合比等除特别说明外均为质量分数或质量比.为62.1%.现场取样CA 砂浆试件的配合比为：m（干料）∶m（乳化沥青）∶m（水）∶m（减水剂）∶m（引气剂）∶m（消泡剂）＝（900～1 150）∶（400～550）∶（30～100）∶（0.5～5.0）∶（1～5）∶（0.05～0.50）.新拌CA 砂浆的J型漏斗流下时间为24s，分离度为0.2%.硬化CA 砂浆的1d抗压强度为0.5MPa，28d抗压强度为2.0 MPa.现场取样CA 砂浆试件的黏度、针入度及延度等均满足《客运专线铁路CRTSⅠ型板式无砟轨道水泥乳化沥青砂浆暂行技术条件》.

1.2 试验过程

采用WDW 系列微机控制电子万能试验机进行试验，由文献［4－5］可知，CA 砂浆的极限抗压强度随加载速率的增大而增大，但其应力－应变曲线形状相似，因此试验采用恒应变控制.参照文献［5］，设计加载速率为0.9mm／min，对应的恒应变速率为3×10－4s－1，每组采用3个试件进行反复荷载试验，另外选取1个试件以相同的恒应变速率进行单调加载试验.若试验离散性过大，则增加试件数量以保证试验数据的有效性.反复荷载试验的等应变增量Δε取为0.015，加载方法参照文献［11－12］进行.

2 试件变形特性分析

现场取样CA 砂浆试件在单调加载与反复荷载情况下的实测应力－应变曲线如图1所示，图中σ为CA 砂浆试件的应力，ε为相应的应变.不同加载情况下试件的极限抗压强度如表1所示.

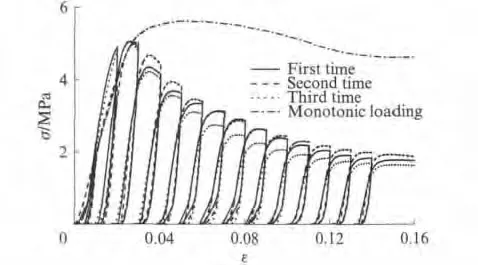
图1 CRTSⅠ型板式无砟轨道CA 砂浆的应力－应变曲线Fig.1 Stress－strain curve of CRTSⅠslab tracks CA mortar

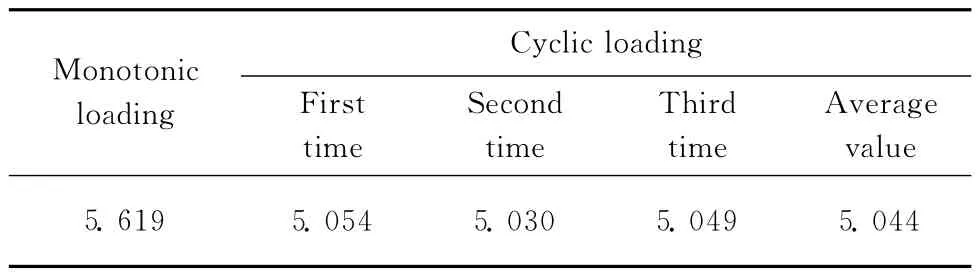
表1 单调加载及反复荷载情况下现场取样试件的极限抗压强度Table 1 Ultimate compressive strength under monotonic loading and cyclic loading MPa

由图1，表1 可知，单调加载情况下现场取样CA 砂浆试件的极限抗压强度为5.619MPa，而在反复荷载情况下其极限抗压强度平均值为5.044MPa，即现场取样CA 砂浆试件单调加载下的极限抗压强度较反复荷载下的极限抗压强度大.两种加载情况下现场取样CA 砂浆试件的极限抗压强度均较文献［4］中室内CA 砂浆试件测出的数值大，这可能是由于现场取样CA 砂浆充填层在灌注过程中不仅添加了铝粉膨胀剂而且还有灌注袋的约束作用，另外现场取样CA 砂浆试件的龄期也较长，从而导致其极限抗压强度增大.由图1还可看出，现场取样CA 砂浆试件在单调加载下应力达到峰值后下降缓慢，而在反复荷载作用下应力达到峰值后下降迅速，当应变值达到0.16时，不论是在单调加载还是反复荷载作用下现场取样CA 砂浆试件仍具有一定的承载能力，这说明其具有良好的韧性与延展性.

将图1的坐标改用相对应力U 和相对应变S，U＝σ／σ0，S＝ε／ε0，其中σ0和ε0分别为极限抗压强度和极限抗压强度对应的应变，σ和ε 分别为任一时刻的应力和该应力对应的应变，处理后的应力－应变曲线如图2所示.由于CA 砂浆是典型的黏弹性材料，在荷载作用下，CA 砂浆呈现柔性破坏，出现明显的裂纹，试件最后保持良好的完整性.不同加载情况下试件的典型破坏情况如图3所示.由图3可见，反复荷载下CA 砂浆的开裂程度较单调荷载下严重，这说明CA 砂浆在反复荷载作用下的累积损伤更加严重.这是由于CA 砂浆是黏弹性材料，其应力应变存在滞后效应，在反复荷载作用下CA 砂浆的微裂缝不断发展，形成宏观裂纹，同时形成的宏观裂纹能继续扩展，而在单调荷载下CA 砂浆的裂纹不能得到充分发展.反复荷载下的主要变形参数有残余塑性应变、公共点应变等.

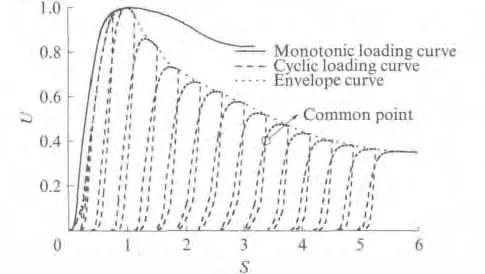
图2 CA 砂浆应力－应变全曲线Fig.2 Complete stress－strain curve of CA mortar

图3 CA 砂浆典型破坏情况Fig.3 Typical damage of CA mortar

2.1 残余塑性应变

荷载卸载至0时的应变称为残余塑性应变，其值大小由材料自身的塑性特性及损伤变形决定.由图1，2可以看出，当荷载小于最大荷载时，卸载路径接近直线，残余塑性应变较小，随着开始卸载点应变的增大，残余塑性应变逐渐增大，这说明CA 砂浆内部出现了伤损及不可恢复变形.

CA 砂浆在反复荷载下，残余塑性应变与开始卸载点应变间的关系如图4所示.图4中：Sc为残余塑性应变与峰值应力处应变的比值；Sx为开始卸载点应变与峰值应力处应变的比值.由图4 可知，CA 砂浆在反复荷载作用下的残余塑性应变与开始卸载点应变大致呈线性关系，可采用下式表示：

式中：A＝0.999 05；B＝－0.348.式（1）能很好地拟合残余塑性应变与开始卸载点应变的关系.随着反复荷载次数的增加，CA 砂浆的残余塑性应变与开始卸载点应变均不断增大，两者呈线性关系，但直线并不经过原点.其原因是CA 砂浆在低应变量的情况下基本没有残余变形，而此时开始卸载点处有一定的应变，因此直线不经过原点.随着加载次数的增多，CA 砂浆内部的损伤稳定持续发展，从而使得CA 砂浆的残余塑性应变与开始卸载点应变呈线性关系.

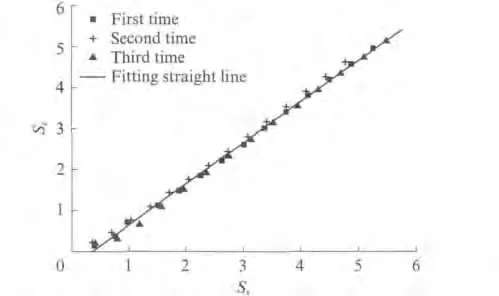
图4 残余塑性应变与开始卸载点应变关系Fig.4 Relationship between residual plastic strain and strain of beginning unloading point

2.2 公共点应变

在反复荷载应力－应变曲线中，把卸载曲线与加载曲线的交点称为公共点（见图2）.Sinha等［13］认为公共点轨迹的峰值应力约等于临界荷载时的应力，即临界应力.由图2可知，再加载曲线的斜率过了公共点以后显著减小，即应力增加不多而应变增长迅速，这表明试件中的已有裂缝在不断扩展或有新裂缝形成，损伤累积加大.故公共点的轨迹可作为一个界限，当应力超过此轨迹时CA 砂浆就会产生新的损伤.公共点应变总小于开始卸载点应变，对于反复荷载模式，公共点处于相对稳定的位置，它决定着卸、加载曲线的形状.全部公共点应变与开始卸载点应变呈线性关系，见图5.图5 中Sg为公共点应变与峰值应力处应变的比值；由图5可见，公共点应变总小于开始卸载点应变，且有：

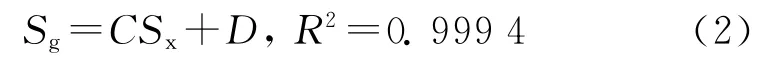
式中：C＝0.992 74；D＝0.014 85.

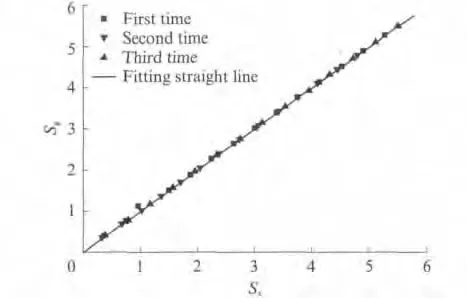
图5 公共点应变与开始卸载点应变的关系Fig.5 Relationship between strain of common point and strain of beginning unloading point

3 反复荷载应力－应变曲线方程

CA 砂浆在反复荷载下的力学性能主要表现为卸、加载曲线方程.在建立卸、加载本构模型时，宜选用形式简便、参数较少的数学表达式，根据材料性能对个别参数的调整不影响所描述曲线的本质特征，这样有利于进行参数和本构模型的分析.

3.1 反复卸载应力－应变曲线方程

当加载的应变小于峰值应力对应的应变时，卸载路径接近直线；但当加载的应变大于峰值应力对应的应变后，卸载路径变为曲线，且随着开始卸载点应变的增大，卸载曲线斜率逐渐减小.假定卸载路径为直线，则有：

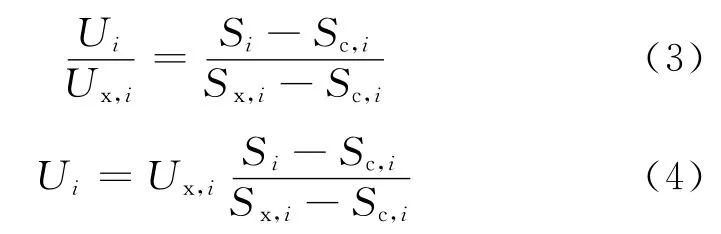
由于随着开始卸载点应变的增大，卸载路径变为曲线，因此本文选用幂函数表示，即：

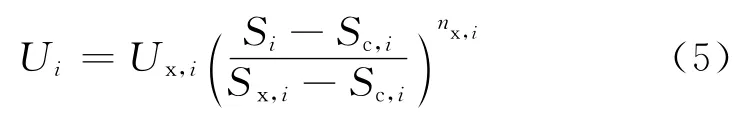
式中：Ui为第i次卸载时卸载曲线上任一点处的相对应力；Ux，i为第i次卸载时开始卸载点处的相对应力；Si为第i次卸载时卸载曲线上Ui对应的相对应变；Sc，i为第i次卸载时的残余塑性相对应变；Sx，i为第i次卸载时开始卸载点处的相对应变；nx，i为第i次卸载时的卸载指数，

以第2次卸载试验数据为例，全部卸载曲线理论值与试验值比较如图6 所示.由图6 可知，拟合曲线与试验数据吻合较好，可以用式（4）～（5）描述CA 砂浆在反复荷载情况下卸载的应力－应变曲线.

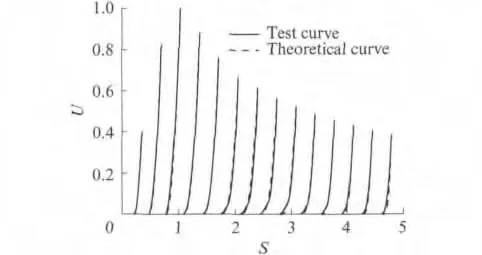
图6 全部卸载曲线Fig.6 All curves of unloading

3.2 反复加载应力－应变曲线方程

试验发现，在反复荷载循环中，再加载曲线的起始点应变与卸载至零时的残余塑性应变值不相等，再加载曲线起始点应变总小于卸载至0N 时的瞬时残余应变值（见图7）.这是由于CA 砂浆卸载后存在弹性后效，即部分瞬时残余应变恢复了变形.

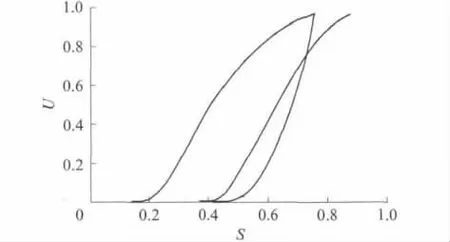
图7 加载曲线示意图Fig.7 Schematic diagram of loading curve

经过分析CA 砂浆的反复加载曲线形状后发现，再加载曲线在公共点之前和之后表现出不同的变化规律.再加载曲线方程可分3段表示：加载曲线上的应变小于公共点应变时假定加载曲线为直线，公共点至每次加载的峰值应力处应变假定为幂函数，在此之后假定加载曲线为直线，即有：

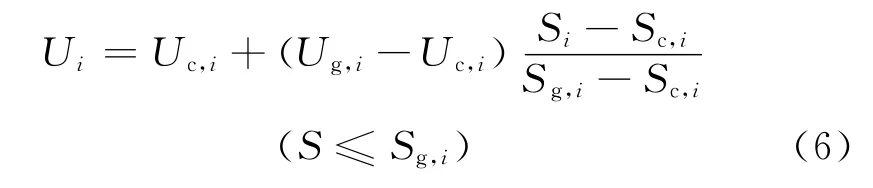
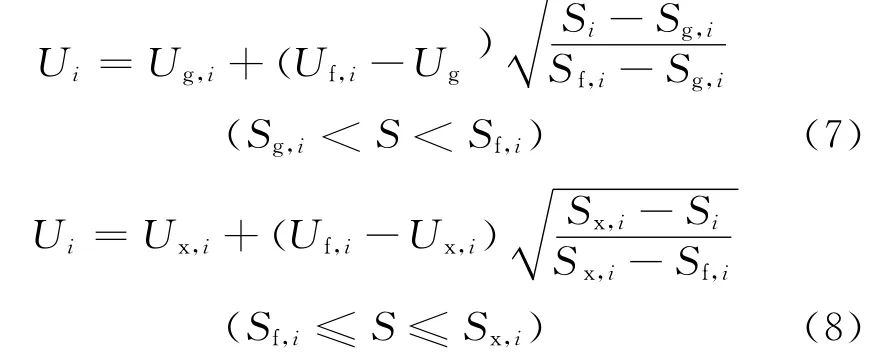
式中：Uc，i指第i次卸载时的残余塑性应力与极限抗压强度的比值；Ug，i指公共点处的应力与极限抗压强度的比值；Sg，i指公共点处的应变与极限抗压强度对应的应变比值；Uf，i指第i 次加载曲线上的峰值应力与极限抗压强度的比值；Sf，i指峰值应力对应的应变与极限抗压强度对应的应变比值。理论再加载曲线与试验结果的比较见图8。由图8 可知，拟合曲线与试验结果吻合较好，可用式（6）～（8）描述CA砂浆的再加载应力－应变曲线。

3.3 试验验证

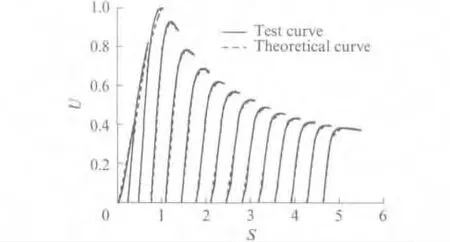
图8 全部加载曲线Fig.8 All curves of loading

图9（a）为应变速率3×10－4s－1下现场取样CA砂浆试件的反复荷载试验曲线与理论曲线的比较，图9（b）为应变速率1×10－3s－1下现场取样CA 砂浆试件的反复荷载试验曲线与理论曲线的比较.由图9可知，该CA 砂浆在反复荷载情况下，不论采用何种应变速率，其理论反复荷载曲线与试验曲线均吻合较好，因此式（4）～（8）能较真实地反映该CA砂浆在反复荷载下的力学特性.

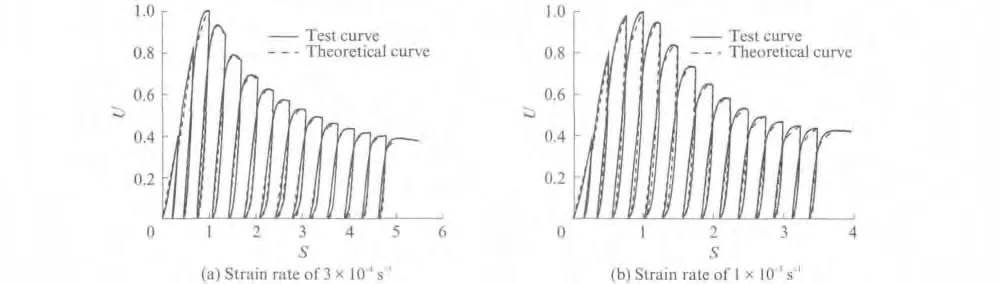
图9 反复荷载试验曲线与理论曲线的比较Fig.9 Comparison of cyclic loading test curve and theoretical curve

4 结论

（1）CA 砂浆在反复荷载下的应力－应变包络曲线与单调荷载下的应力－应变全曲线相比，其上升段基本一致，其下降段在反复荷载作用下下降较快，这说明反复荷载下对CA 砂浆造成的不可恢复损伤较大.

（2）根据反复荷载试验结果，建立了CA 砂浆反复荷载曲线方程，这些数学表达式能较真实地反映CA 砂浆在低周反复荷载下的力学特性，反复荷载理论曲线与试验曲线能较好吻合.

［1］COENRAAD E.Recent development in slab track［J］.European Railway Review，2003，9（2）：81－85.

［2］SHIGERU M，HIDEYUKI T，MASAO U，et al.The mechanism of railway tracks［J］.Japan Railway and Transportation Review，1998，15（3）：38－45.

［3］KATSUOSHI A.Development of slab tracks for Hokuriku Shinkansen line［J］.Quarterly Report of RTRI，2001，42（1）：35－41.

［4］谢友均，曾晓辉，邓德华，等.铁路无砟轨道水泥乳化沥青砂浆力学性能［J］.建筑材料学报，2010，13（4）：483－486.XIE Youjun，ZENG Xiaohui，DENG Dehua，et al.Mechanical characteristics of China railway track system（CRTS）Ⅰtype slab tracks CA mortar under different strain rates［J］.Journal of Building Materials，2010，13（4）：483－486.（in Chinese）

［5］王发洲，刘志超，胡曙光.加载速率对CA 砂浆抗压强度的影响［J］.北京工业大学学报，2008，34（10）：1059－1065.WANG Fazhou，LIU Zhichao，HU Shuguang.Influence of loading rate on compressive strength of CA mortar［J］.Journal of Beijing University of Technology，2008，34（10）：1059－1065.（in Chinese）

［6］王涛.高速铁路板式无碴轨道CA 砂浆的研究与应用［D］.武汉：武汉理工大学，2008.WANG Tao.Research and application on CA mortar in ballastless slab track of high speed railway［D］.Wuhan：Wuhan University of Technology，2008.（in Chinese）

［7］王涛，胡曙光，王发洲，等.CA 砂浆强度主要影响因素的研究［J］.铁道建筑，2008（2）：109－111.WANG Tao，HU Shuguang，WANG Fazhou，et al.The main factors influencing strength of cement asphalt mortar［J］.Railway Engineering，2008（2）：109－111.（in Chinese）

［8］谭忆秋，欧阳剑，王金凤，等.CA 砂浆强度影响因素及强度机理研究［J］.哈尔滨工业大学学报，2011，43（10）：80－83.TAN Yiqiu，OUYANG Jian，WANG Jinfeng，et al.Factors influencing strength of cement asphalt mortar and strength mechanism［J］.Journal of Harbin Institute of Technology，2011，43（10）：80－83.（in Chinese）

［9］田冬梅，元强，朱蓉，等.水对水泥乳化沥青砂浆静态力学性能的影响［J］.硅酸盐学报，2012，40（11）：1544－1552.TIAN Dongmei，YUAN Qiang，ZHU Rong，et al.Effect of water on static mechanical properties of cement emulsified as－phalt mortar［J］.Journal of the Chinese Ceramic Society，2012，40（11）：1544－1552.（in Chinese）

［10］WANG Li，WANG Ping，ZENG Xiaohui，et al.The effect of temperature on the mechanical properties of CA mortar［C］∥Advanced Materials Research.Clausthal－Zellerfeld：Trans Tech Publications，2012：860－864.

［11］过镇海，张秀琴.混凝土在反复荷载作用下的应力－应变全曲线［J］.冶金建筑，1981（9）：14－17.GUO Zhenhai，ZHANG Xiuqin.The complete stress－strain curve of concrete under repeated loading［J］.Metallurgical Construction，1981（9）：14－17.（in Chinese）

［12］邓宗才，孙成栋.钢纤维混凝土在低周反复荷载下力学性能的研究［J］.工程力学，2001，18（3）：105－110.DENG Zongcai，SUN Chengdong.On properties of steel fiber reinforced concrete under cyclic loading［J］.Engineering Mechanics，2001，18（3）：105－110.（in Chinese）

［13］SINHA B P，GERSTLE H K，TULIN L G，et al.Stress－strain relationships for concrete under cyclic loading［J］.ACI Journal Proceedings，1964，61（2）：195－212.