机非混行交叉口右转机动车通行能力研究*

梁春岩 吴立新 冯天军

(吉林建筑大学交通科学与工程学院，长春 130118)

0 引言

迄今为止，关于通行能力的研究成果较多.针对信号控制交叉口，通行能力的计算方法有HCM法、TRRL法、停车线法和冲突点法，而无信号控制交叉口的方法有间隙接受理论、车队分析法、延误分析法和综合计算法［1］.针对机非混行条件下的机动车通行能力的研究，由于发达国家自行车流量极小，并没有做太多的研究，仅仅是根据实际情况，提出自行车对交叉口通行能力和饱和流率的影响因素和修正方法［2－4］.

国内对于自行车对机动车道通行能力的影响积累了一定的理论成果.主要集中在自行车交通流对交叉口机动车通行能力的影响及相应的计算模型，通过实际数据的验证，找出最适合于混合交通交叉口通行能力的计算方法，得出不同自行车交通量情况下交叉口综合治理最佳方案［5－8］.同时，国内外专家均已认识到，在自行车流量较大的条件下，现行方法严重地高估了道路平面交叉口的通行能力［9］.

在诸多成果中，专门针对右转机动车道通行能力的研究几乎没有，直行和左转机动车的研究成果可以借鉴用于研究右转机动车通行能力.对于自行车较多交叉口，右转机动车与自行车的冲突非常严重，这是不可忽略的研究部分.而左转自行车在信号控制交叉口多采用二次过街方式，因此本文仅以右转机动车与直行自行车的冲突机理为基础，应用间隙理论建立不同相位信号控制交叉口右转机动车通行能力计算模型.

1 间隙理论

间隙理论是分析无信号交叉口的基本理论，按照主路优先控制的通行规则，次要道路上的车辆必须等主要道路车流间出现足够的可穿越空挡时才能通过.交叉口主要道路进口道的通行能力几乎和路段的通行能力一样，根据计算主要道路上车流中可供次要道路车辆穿越的空档数来求出次要道路可通行的最大交通量.假设主要道路车流按照泊松分布到达，可建立计算次要道路可通过的最大交通量的公式如下［10］:

式中，Q'max为次要道路可能通过最大交通量，辆/h;Q为主要道路交通量，辆/h;q为Q/3600(辆/s);τ为次要道路可以穿过主路车流的临界空挡时距，s，小轿车的临界间隙在4.5s～10s之间变化;h为次要道路车辆的车头时距，s，按小轿车一般取2s～3s.

在描述间隙理论中，经常假设驾驶员具有一致性和相似性.驾驶员的一致性是指在所有类似的情况下，在任何时刻其行为方式相同，而不是先拒绝一个间隙随后又接受一个较小的间隙;相似性则是期望所有驾驶员的行为是严格的同一方式.本文的研究同样基于这样的假设.

2 模型建立

在右转机动车与直行自行车发生冲突时，直行自行车具有优先权，看成主路，右转机动车必须等直行自行车流中出现可穿越间隙时才能通行，将其看成次要道路，可以利用间隙理论计算右转机动车通行能力.

2.1 两相位信号控制交叉口

对于两相位信号控制交叉口，南北方向为相位1，其绿信比为λ1;东西方向为相位2，其绿信比为λ2，自行车交通流信号配时方案与同方向的机动车相同.以南进口为例，右转机动车需等南进口或者西进口的自行车交通流出现可供穿越的空挡后才能通过交叉口，冲突示意图如图1所示.

仍以南进口为例，根据间隙理论得右转机动车的通行能力为:

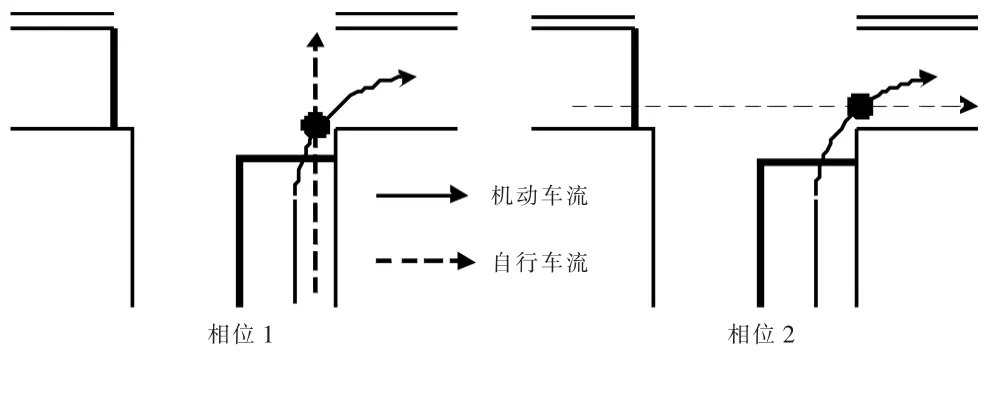
图1 右转机动车与直行自行车冲突示意图

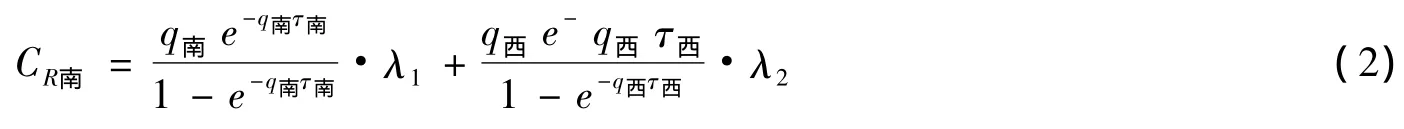
式中，CR南为南进口右转机动车通行能力，v/s;q南为南进口直行自行车流量，bike/s·m;τ南为南进口右转机动车穿越南进口直行自行车流的临界间隙，s;h南为南进口右转机动车穿越南进口直行自行车流的跟随时间，s;q南为西进口直行自行车流量，bike/s·m;τ西为南进口右转机动车穿越西进口直行自行车流的临界间隙，s;h西为南进口右转机动车穿越西进口直行自行车流的跟随时间，s.

同理，可得其他进口道右转机动车通行能力:

设所有进口道的右转机动车穿越直行自行车流的临界间隙和跟随时间相等，令τ东=τ西=τ南=τ北τ，h东=h西=h南=h北=h，经过整理有交叉口右转机动车通行能力为:

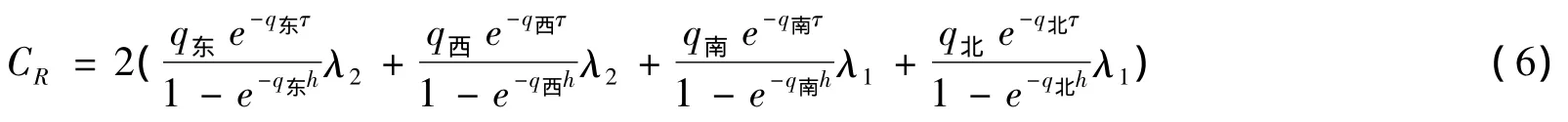
如果相交的两条道路等级相当，且交通量差异不大，假设λ1=λ2=1/2，则(6)式可简化成:

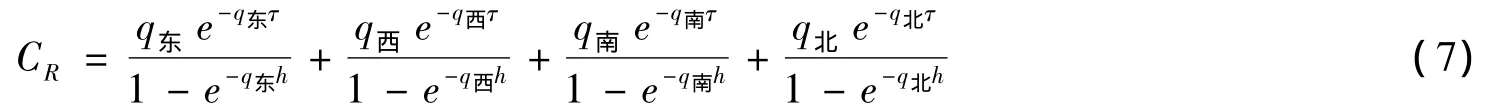
2.2 四相位信号控制交叉口

对于四相位信号控制交叉口，南北方向直行相位称为相位1，其绿信比为λ1;南北方向左转相位称为相位2，其绿信比为λ2;东西方向直行相位称为相位3;其绿信比为λ3，东西方向左转相位称为相位4，其绿信比为λ4.右转机动车在相位1和相位3通行时的冲突情况与两相位信号控制交叉口相同，在相位2和相位4通行时，没有冲突交通流，仍以南进口为例，右转机动车通行能力为:

式中，hR为右转机动车以饱和状态通过交叉口时的车头时距，s;其他参数含义同上.

同理可得其他进口道右转机动车通行能力:

这里同样假设临界间隙为τ，跟随时间为h，则四相位信号控制交叉口右转机动车通行能力为:

3 模型验证

以石家庄市裕华路与平安大街交叉口的裕华路西进口为例，该交叉口为两相位信号控制，共观测8个信号周期，验证的相关数据如表1所示.其中，右转机动车穿越直行自行车流的临界间隙τ=2.8，跟随时间h=2.6［11］，右转机动车实际通行能力应用(10)式计算:

式中，hR含义同上.

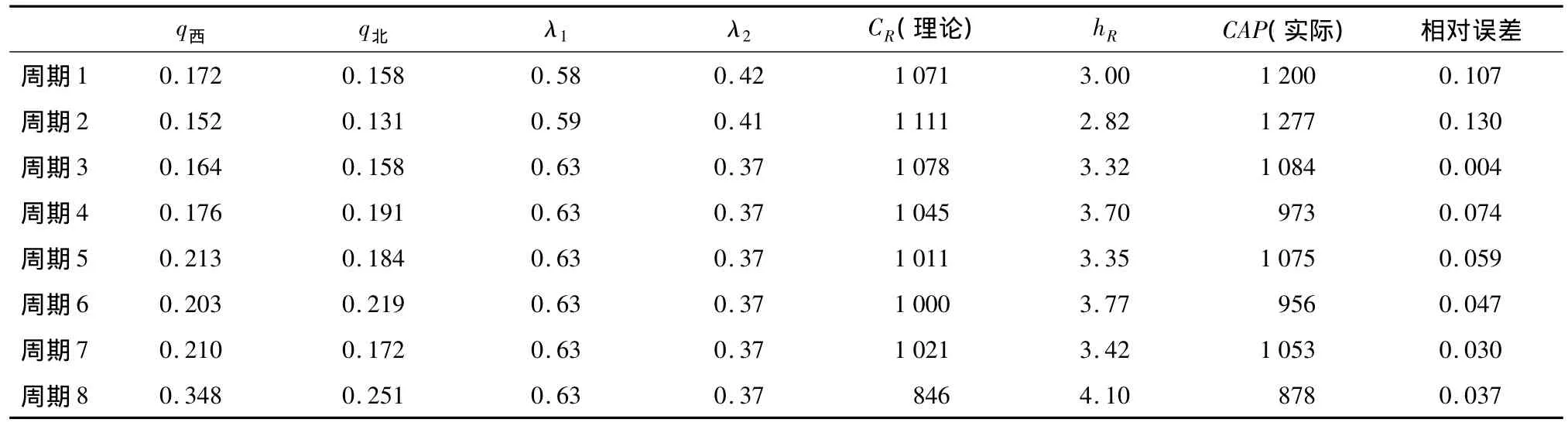
表1 通行能力验证

通过验证数据可以看出，理论通行能力与实际通行能力的误差多数都在10%以下，平均误差为6.1%，误差较小，满足精度要求，结果证明模型可靠.

4 结语

本文以右转机动车与直行自行车冲突为基础，应用间隙理论，建立了机非混行交叉口右转机动车道通行能力计算模型，并应用石家庄实际调查数据进行验证，平均误差为6.1%，结果表明模型可靠.该模型需要的数据基础简单且容易获得，具有较强的实用价值，丰富了右转机动车通行能力的研究成果，对研究机非混行交叉口具有一定的参考意义.模型仅针对石家庄市两相位信号控制交叉口的西进口进行了验证，不同地区的其他信号控制方式及其他进口道需要进一步验证.

［1］陈宽民，严宝杰.道路通行能力分析［M］.北京:人民交通出版社，2003:133－137，169－179.

［2］Allen，P.，J.Hummer，N.Rouphail，and J.Milazzo.The Effect of Bicycles on Capacity of Signalized Intersections［J］.Transportation Research Record，1998，1646(1):87 －95.

［3］Brilon W，Wu N.Delays at fixed time traffic signals under time depent traffic conditions［J］.Traffic Engineering and Control，1990，31(3):623－628.

［4］Perez，Tarko.Calibration of Capacity Parameters for Signalized Intersections in Indiana［J］.Journal of Transportation Engineering，2005，131(12):904－911.

［5］徐良杰，王 炜.左转自行车对直行机动车通行的影响分析模型［J］.东南大学学报，2005，35(5):805－809.

［6］徐立群，吴 聪，杨兆升.信号交叉口通行能力计算方法［J］.交通运输工程学报，2001，1(1):82－85.

［7］李建新，毛保华.混合交通环境下有信号平面交叉口通行能力研究［J］.交通运输工程与信息，2001，1(2):119－123.

［8］王殿海，金 勇，陈永恒.提前右转机动车的通行能力［J］.吉林大学学报(工学版)，2005，35(5):467－472.

［9］Transportation Research Board.Highway Capacity Manual，4th ed［M］.National Research Council，Washington，D.C.，2000:11 －15.

［10］王殿海.交通流理论［M］.北京:人民交通出版社，2002:124.

［11］梁春岩，王春光，沈 战，王殿海.机非混行交叉口右转机动车行程时间计算方法［J］.吉林大学学报(工学版)，2007，37(5):1053－1057.