环境空气质量综合指数计算方法比选研究
2014-10-12潘本锋张建辉解淑艳宫正宇
王 帅,潘本锋,张建辉,解淑艳,宫正宇,李 亮
中国环境监测总站,国家环境保护环境监测质量控制重点实验室,北京 100012
环境空气质量综合评价方法选取对于环境管理具有重要的决策引导作用,常用的空气质量综合评价方法主要有综合指数法[1-2]、灰色聚类法[3]、模糊综合评判法[4]、主成分分析法[5]、人工神经网络法[6]等。其中,综合指数法具有计算简单、指标覆盖全面的优点,在环境管理中被广泛应用于不同城市间空气质量的比较或同一城市空气质量的变化趋势分析;其他几种方法在科学研究中有所使用,但在环境管理中的实际应用并不多见。由于与空气质量标准相关联,综合指数法中的单项指数还可应用于制定空气质量分级标准。在《环境空气质量标准》(GB 3095—2012)[7]发布前,环境空气质量综合指数主要包括二氧化硫、二氧化氮、可吸入颗粒物等3项指标,对于当前新开展监测的细颗粒物、臭氧、一氧化碳等指标应如何纳入综合指数,仍缺乏充分的研究论证。在综合指数法中,各污染物均使用评价浓度除以质量标准中的浓度限值进行标准化,再按照等权重进行求和。但由于不同污染物间具有一定的关联性,因此综合指数法会有一定的信息冗余,部分污染物的实际权重可能会被放大。另外,综合指数计算过程中各项污染物评价浓度选取方法和评价标准的差异也会影响污染物的实际权重和信息冗余情况,有必要对这一现象进行深入分析,使得所采用的评价方法符合环境管理的需求。主成分分析法与其他方法相比的优点是指标权重的确定较为客观,在环境空气质量综合评价中有不少应用[8-9]。研究提出了4种备选综合指数计算方法,并采用主成分分析技术对不同综合指数计算方案下污染物的权重系数进行了分析,提出了适合中国当前环境管理需要的综合指数计算方法,为有关科学研究和环境管理提供借鉴。
1 实验部分
1.1 材料
数据来自74个实施环境空气质量新标准城市2013年6项污染物逐月统计数据,污染物浓度统计方法依据《环境空气质量评价技术规范(试行)》[10]中有关规定。污染物统计指标如表1 所示,SO2、NO2、PM10、PM2.5的统计指标均为月均值浓度,CO的统计指标为月均值或日均值95百分位数浓度,O3统计指标为日最大8 h值的月均浓度或90百分位数浓度。6项污染物统计指标分别按照各自在《环境空气质量标准》(GB 3095—2012)中的浓度限值进行标准化。根据统计指标和参比标准的差异,共提出4种备选标准化方案。

表1 不同综合指数计算方案下污染物的标准化方法
1.2 方法
定义单项指数占综合指数比例最大的污染物为主要污染物,对不同的综合指数计算方案分别统计逐月的主要污染物情况。同时对各项污染物统计指标间的相关关系进行全年和逐月分析。
为了研究不同计算方案下各污染物的最优权重系数,以主成分分析方法的结果为参比进行比选研究。主成分分析技术主要被用于在保证较小的信息损失下通过选择较少的新指标来代替原始指标,经过线性变换以较少的综合变量来代替原来的多维变量,从而起到减少信息冗余和信息噪音的目的。分析方法:设有n个样本,每个样本有p项污染物,构成 n × p阶矩阵 Xi×j(i=1,2,…,n;j=1,2,…,p)。首先对矩阵 Xi×j的 p 个列向量进行标准化,使其成为均值为0、方差为1的列向量,记为 Zij(i=1,2,…,n;j=1,2,…,p)。然后求出其相关系数矩阵R,并求R的p个特征根λj(j=1,2,……,p)和对应的特征向量 Ej=(e1j,e2j,……,epj)T。构造的新特征向量彼此不相关。以特征根为权重计算各特征向量的贡献率:
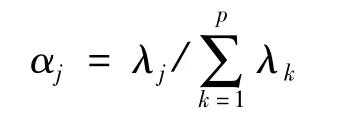
在经典主成分分析方法中,通常是选取累积贡献率大于85%的最少数量的特征变量为指标来进行综合评价,从而起到减少指标维度的目的。但研究的目的是对不同综合指数计算方案的信息冗余情况进行比较,并不是用于降低指标维度,因此将累积贡献率设为100%,即保留所有的特征向量信息。将p个特征向量按照其权重不同,进行列向量加权求和,得出新的综合向量:

该综合向量代表了给定的统计指标下各项污染物的最优系数,以最优系数为权重计算综合指数能够在不损失信息的前提下去除冗余信息。将主成分分析中的标准化方法与表1中标准化方法进行简单数值变换后就可以得出不同计算方案下的优化系数。各项污染物的优化系数均以PM2.5系数为1进行归一化得出最优权重系数。
数据分析和处理使用 Matlab、SPSS、Excel软件完成。
2 结果与分析
2.1 主要污染物逐月变化情况
图1为不同综合指数计算方案下74个城市逐月主要污染物的分布情况。

图1 不同综合指数计算方案下逐月主要污染物频率分布情况
从图1可以看出,以SO2为主要污染物的频率很小,仅在 1、2、11、12月的个别城市出现过。以CO为主要污染物的频率也很小,仅方案3中个别城市在 2、3、11、12 月出现过。说明 SO2、CO污染物浓度较低,在不同计算方案下都不是主要污染物,而以 PM2.5、O3、PM10、NO2为主要污染物的频率相对较大,表明这4类污染物是目前影响中国环境空气质量的主要污染物。不同方案之间以 NO2、PM2.5、PM10为主要污染物的频率大体呈现出方案3≤方案1≤方案2≤方案4的规律,而以O3为主要污染物的频率呈现相反的变化趋势。不难看出,这是由于计算指数时 NO2、PM2.5、PM10选用的参比标准逐渐加严而O3选用的参比标准逐渐放宽导致的。从逐月的变化规律来看,以PM2.5为主要污染物的频率在冬季最高,夏季最低;以PM10为主要污染物的频率在4月最高,6、7月最低;以O3为主要污染物的频率在夏季最高,冬季最低。
由图1可知,在方案3中以O3为主要污染物的频率较高,在7、8月约90%城市以 O3为首要污染物,而在冬季1、2月仍有近16%城市以 O3为首要污染物。方案4中,O3的作用被过分低估,在5—8月等 O3污染较重的时段仅有不到5%的城市以O3为主要污染物。可以看出,方案3、方案4均不能客观反映中国O3污染状况,方案1、方案2是相对合理的备选方案,能够合理地反映出O3的逐月变化规律。
2.2 不同综合指数计算方案下的优化权重系数
利用主成分分析技术统计得出的优化权重系数如图2所示,均以PM2.5系数为1进行了标准化。

图2 不同计算方案下各项污染物逐月优化系数
优化权重系数的确定考虑了6项污染物间的信息相关性和重叠性,优化系数大于1时表明该污染物应有更高的权重,即现有综合指数计算方法中该污染物的权重有所低估,出现信息缺失;当优化系数小于1时表明该污染物应有更小的权重,即现有综合指数计算方法中该污染物的权重偏高,出现信息冗余;当优化系数小于0时,表明该污染物并不适合作为判定污染的指标。由于污染物浓度变化具有明显的月际特征,因此同一种污染物在不同月份的最优权重系数也有一定的波动性。
从PM10优化权重系数来看,4种方案下的PM10优化系数主要在0.5~1.5范围内波动,信息缺失和信息冗余情况基本保持平衡。从 SO2、NO2、CO优化权重系数来看,4种方案下 SO2、NO2、CO逐月权重系数主要分布在大于1的范围,表明4种方案对这3项污染物浓度变化信息均反映不足。从O3优化权重系数来看,4种方案下的O3优化系数均出现了较为剧烈的月际变化,4—8月O3优化系数主要分布在大于1区域,表明4种方案的综合指数应给予O3更大的权重,而其他月份(如1—3月)O3的权重系数小于零,4种方案均存在O3信息冗余的现象,特别是方案1和方案4的信息冗余情况较为严重。
将每种计算方案下的逐月优化权重系数进行算术平均,得到不同方案下各污染物的平均权重系数(表2)。在不同方案中SO2的平均权重系数为1.96~2.89,NO2的平均权重系数为 1.89~2.38,CO的平均权重系数为2.05~4.24,这3种污染物的优化权重系数明显大于1,表明4种计算方案中这3种污染物的实际权重都偏小。PM10的平均权重系数为1.08~1.17,与4种综合指数计算方案中的系数基本一致。O3的平均权重系数为 -1.33~0.43,优化权重系数明显小于1。即在去除冗余信息后,SO2、NO2、CO的权重得到相对强化,PM2.5、PM10的权重被相对削弱,O3的权重在夏季得到强化,在冬季被削弱。

表2 不同方案下各项污染物的平均优化权重系数
各方案下PM10、SO2、NO2的平均权重系数较为接近,从这方面难以区分不同方案的优劣。但方案1、方案4中 O3平均优化权重系数均小于零,特别是在1—3月O3污染较轻的月份给予了过高的权重,从这个角度来看方案 2、方案 3更优。
3 讨论
由4种计算方案中污染物平均权重系数和逐月主要污染物频率分布情况可以看出,方案2是相对较优的综合指数计算方法。但在传统的综合指数计算方法中,不同污染物采用了等权重方案。
而实际上由于污染物间有着复杂的相关性,传统的综合指数计算方法可能会存在一定的信息冗余。主成分分析技术作为一种降维处理方法,能够去除信息噪音和信息重复,最大限度地保留系统信息。根据主成分分析结果,方案2中SO2、NO2、PM10、CO、O3、PM2.5的平均权重系数分别为2.31、2.38、1.09、4.09、0.42、1.00。这一权重系数与污染物浓度间的相关性有密切关系。
表3为城市污染物月统计指标间的Pearson相关系数,可以看出 SO2、NO2、CO、PM2.5、PM105种污染物间均呈现极显著正相关关系,逐月的相关系数亦基本类似(结果略),其中 PM2.5和 PM10的相关性最好。这种显著正相关关系可解释为不同污染物排放的同源性,如各种生产、生活活动均同时排放多种污染物。而对于 PM2.5、PM10来说,PM2.5是PM10其中一部分,所以有着高度的相关性。在经过冗余信息处理后,两者的权重被相对弱化,即 PM2.5与 PM10的总权重(2.09)与 SO2、NO2的权重基本相当。
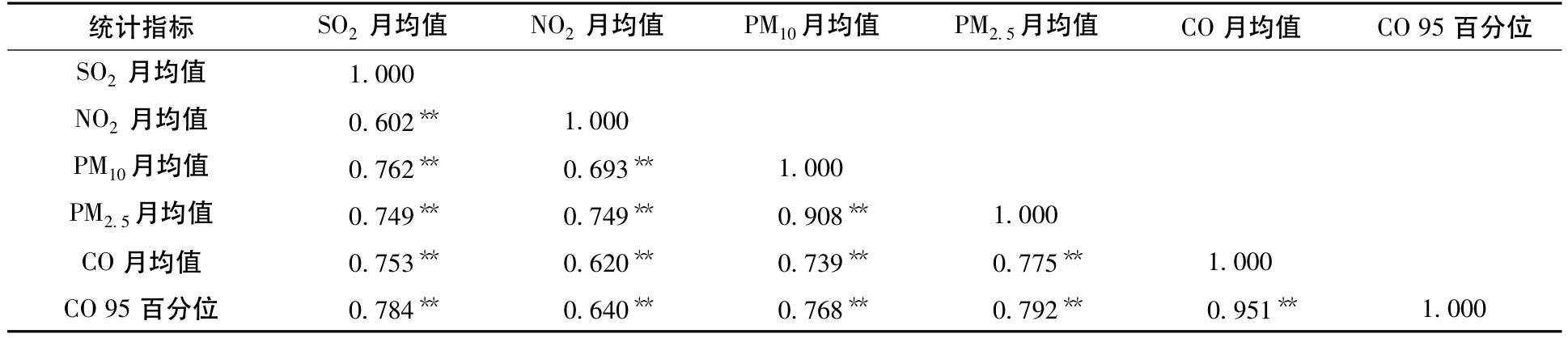
表3 各污染物月统计指标的Pearson相关系数
O3与其他5种污染物的相关关系较复杂(表4),1月O3统计量与其他污染物统计量间呈显著负相关关系,7月 O3统计量与除CO外其他污染物统计量间呈显著正相关关系,但4、10月均不存在类似的相关关系。这一现象与O3的季节性污染特征有关,夏季光照强度大,为光化学反应创造了条件,O3的生成量与前体物浓度水平存在正相关关系;而冬季光照强度弱,即使前体物浓度水平较高,O3的生成速率主要受到光照条件的限制,不受前体物浓度水平控制。因此在冬季时,颗粒物浓度低、空气质量较好的城市,由于光照条件好其O3浓度可能会高于其他颗粒物污染重的城市。正是由于这种复杂的相关关系,使得O3逐月优化权重系数出现明显的季节变异特征。例如冬季O3与其他主要污染物间呈负相关关系,其优化权重系数为负值,表明冬季O3并不适合作为评价污染状况的指标;而夏季O3与其他主要污染物间呈正相关关系,其优化系数变为正值,是度量空气质量 状况的有力指标。

表4 不同月份O3统计指标与其他污染物指标的Pearson相关系数
虽然主成分分析方法能够给出更为客观和精确的综合评价结果,帮助管理者理清不同评价方法下污染物间内在的权重关系,但在实际环境管理应用时显得过于复杂。且由于主成分分析方法的标准化参数是逐月变化的,无法用于逐月环境空气质量状况的同比和环比分析,采用统一的标准化方法和计算公式符合环境管理的需求。另外,环境空气质量综合评价方法的选取除注重科学性和客观性外,还要特别注意对环境管理和环境决策的引导性,两者有时不能完全一致。例如某些污染物的城市间浓度差异较大,从信息识别角度讲很有价值,但若大多数城市污染物浓度均满足标准限值要求时,这种浓度差异对于环境管理的价值是有限的;而对于某些浓度较高但城市间浓度差异相对较小的污染物,从信息识别角度来讲价值并不高,却是环境管理和决策中应该重点强调的。
传统综合指数计算方案中SO2、NO2、CO的权重与主成分分析方法优化后的权重相比偏低,但由于中国当前主要大气污染物是PM2.5、PM10、O3,降低SO2、NO2、CO的权重符合环境管理的需求。综上,建议以方案2为计算逐月环境空气综合指数的计算方法,不同污染指标间按照等权重处理。分析方案2计算方案可知,该方案可延伸应用于季度、半年、年度综合指数计算,与《环境空气质量评价技术规范(试行)》中年度评价的有关方法保持一致,使得逐月评价结果与全年评价结果在综合指数数值和排序方面均能够保持一致。将方案2应用于2013年74个城市逐月综合指数计算,并以《环境空气质量评价技术规范(试行)》中方法计算出的年度综合指数作为参比(图3)。可以看出,每个城市逐月的综合指数均在参比值附近波动,其平均值接近于参比值(图中虚线),即逐月综合指数和排名结果与年度综合指数和排名结果是一致的,进一步验证了方案2的适用性。其他方案由于标准化方法发生变化,计算出的逐月综合指数则与参比值有明显的偏差(结果略)。
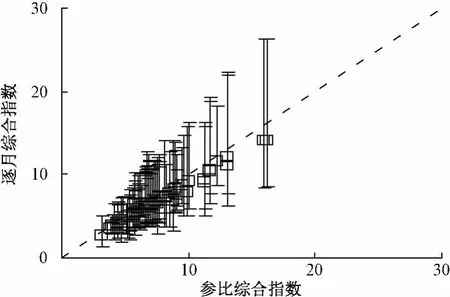
图3 74个城市逐月综合指数平均值和极值与参比综合指数关系(方案2)
方案2与《环境空气质量评价技术规范(试行)》资料性附录3中的参考方法并不完全相同,主要差别是 SO2、NO2、PM10、PM2.5等 4 项污染物的单项指数仅考虑了月均值,而未考虑重污染时期高浓度事件的影响,导致图3中逐月综合指数平均值偏低于参比值。考虑到颗粒物的健康危害主要表现为长期慢性效应[11-12],且中国当前和今后一段时期内颗粒物平均浓度仍将处于较为严重的水平,因此主要强调颗粒物平均浓度这一指标。未来随着空气质量的不断改善和环境管理精度的提高,有必要将高浓度污染事件的影响考虑到评价指标中。
4 结论
1)环境空气质量综合指数计算方法中统计指标和参比标准的变化会对逐月主要污染物的判定有较大的影响,在4种计算方法中 PM2.5、PM10和O3是目前影响中国环境空气质量的主要污染物。
2)主成分分析结果表明,在去除冗余信息后,4种方案中 PM2.5、PM10的权重被相对削弱,SO2、NO2、CO 的权重得到相对强化,O3的权重在夏季得到强化,在冬季被削弱。污染物相对权重变化的原因是污染物间有着复杂的相关性。其中SO2、NO2、PM10、PM2.5和 CO 月统计量间有显著的正相关性,O3与 SO2、NO2、PM10和 PM2.5间的相关性因季节而不同。
3)综合考虑主成分分析结果和中国大气环境管理的实际需求,建议计算逐月环境空气质量综合指数时,SO2、NO2、PM10、PM2.5宜以月均值除以年均值标准进行标准化,CO、O3宜以特定百分位数浓度除以日均值标准(或8 h均值标准)进行标准化。该方法可延伸到季度、半年、年度的环境空气质量综合指数计算。
[1]唐永銮.环境质量综合指数简介[J].环境科学,1979,4(2):71-74.
[2]刘硕,朱建平,蒋火华.对几种环境质量综合指数评价方法的探讨[J].中国环境监测,1999,15(5):33-37.
[3]陈玮.基于灰色聚类与模糊综合评判的空气质量评价-以长江沿岸主要城市为例[D].上海:华东师范大学,2012:7-10.
[4]王陆军,廖晓芬.宝鸡市大气环境质量分析与综合评价[J].西南师范大学学报:自然科学版,2005,30(1):154-157.
[5]豆俊峰,邹振扬.主成分分析法在大气环境质量综合评价中的应用[J].重庆环境科学,2001,23(2):32-33.
[6]何璠.基于BP人工神经网络的环境质量评价模型研究[D].成都:四川大学,2006:33-58.
[7]GB 3095—2012 环境空气质量标准[S].
[8]张曙红,武鹏程.武汉市大气环境质量的综合评价[J].环境科学与技术,2008,31(3):110-113.
[9]杜敏,基于主成分分析法的环境质量综合指数研究[D].成都:四川大学,2006:11-19.
[10]HJ 663—2012 环境空气质量评价技术规范(试行)[S].
[11]王帅,丁俊男,王瑞斌,等.我国环境空气中颗粒物达标统计要求研究[J].环境科学,2014,35(2):401-410.
[12]World Health Organization.Air quality guidelinesglobal update 2005[R].Bonn:WHO Regional office for Europe,2005:275-280.
