混沌时间序列的LSSVM预测方法

莫小琴，李钟慎

（华侨大学 机电及自动化学院，福建 厦门361021）

随着混沌理论研究的不断深入，混沌时间序列预测已成为非常重要的一个研究方向，并广泛应用于信号处理、自动控制等领域［1］.但混沌系统对初值的极端敏感性使其很难进行精确的预测.相空间重构是混沌时间序列预测的基础，重构效果的好坏直接影响着预测的精度.选用互信息法［2］和Cao提出改进的模糊神经网络（fuzzy neural network，FNN）算法［3］分别对相空间重构参数进行确定，能够实现比较好的重构效果.最小二乘支持向量机（least squares support vector machines，LSSVM）是一种新型的预测方法，拥有强大的学习能力，能很好地解决神经网络结构训练时容易陷入局部极小和过拟合等问题［4-5］.但是LSSVM在不同参数作用下，预测性能会有很大的差别.粒子群优化（particle swarm optimization，PSO）是近年来发展比较快的一种简单可行的智能寻优算法，能快速有效地解决如何寻找合适参数的问题［6］.因此，本文在结合相空间重构理论的基础上，提出PSO算法优化的LSSVM的混沌时间序列预测模型，分别对一阶Logistic、二阶Henon、三阶Lorenz等3种典型混沌时间序列进行预测，并与RBF神经网络的预测结果［7］进行比较.

1 时间序列相空间重构

1.1 相空间重构

相空间重构提出从高维的相空间中恢复混沌吸引子［8］.它的思想是系统中任一个分量的演化进程都是由其他与其相互作用的分量决定的，所以通过分析某一分量的一批时间序列数据，能提取和恢复出原系统的规律.根据Takens定理，当吸引子的分形维数为d时，选择合适的延迟时间τ和嵌入维数m，且满足m≥2d+1，对混沌时间序列｛x（t）｝，t＝1，2，…，n进行相空间重构，即

对n步后的预测为

式（2）中：F（·）为构建的预测模型.由F（x（k-m），x（k-m+1），…，x（k-1））和Y（k）＝x（k）组成的样本对，训练并建立LSSVM预测模型，从而完成对混沌时间序列的预测.

1.2 重构相空间参数的选取

相空间重构吸引子的成败在于延迟时间和嵌入维数的选取，并且这2个参数的选取是互不相关的［9］.互信息法是一种有效估计延迟时间的方法.Shaw 提出互信息第一次到达最小时滞时即为延迟时间［10］.定义计算延时时间τ的公式为

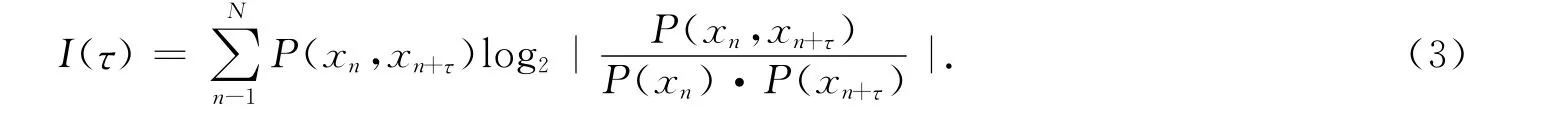
式（3）中：P（xn，xn+τ）为时间序列｛xn｝和｛xn+τ｝的联合概率；I（τ）为某一时间序列包含另一时间序列信息的概率，当I（τ）为第一个极小值时，τ的取值就是最佳的延迟时间.

CAO方法是对FNN算法改进后提出的一种选择最佳嵌入维数的方法［3］.其运算步骤为如下.

在d维空间中，每一个相点矢量X（i）都有一个某距离内的最邻近点NNN（i），两者距离为Rd（i），当维数增加到d+1时，两相点的距离发生变化，则在d+1维相空间中的距离为

若Rd+1（i）远大于Rd（i），可认为这两点是伪邻近点.

CAO方法定义计算嵌入维数的公式为

计算所有a2（i，d）的平均值，得到

计算m维到m+1维的变化，可得

式（7）中：随着m的变化，E1（m）达到饱和，此时，m+1取值就是所求的最佳嵌入维数.

采用这2种方法分别确定的3种典型混沌时间序列的延迟时间（τ）以及嵌入维数（m），如表1所示.通过对比重构吸引子的几何形状与原吸引子之间的相似性，以及不同延迟时间所产生的差异性，可以验证这2种方法选取的参数能够达到比较好的重构效果［8］.

表1 实验参数Tab.1 Experimental parameters

2 基于LSSVM的回归预测

2.1 LSSVM 模型

选取延迟时间τ和最优嵌入维数m后，构造样本数据对

式（8）中：Xi（i＝1，2，…，M）为预测输入数据；yi（i＝1，2，…，M）为对应的输出数据.

对于一个给定的训练样本数据集（Xi，yi）（i＝1，2，…，l），在高维空间中用线性函数拟合样本，可得

式（9）中：wT为二次规划问题解的矩阵；φ（·）为非线性映射关系函数；b为常值偏差.

时间序列的数据集被非线性映射函数φ（·）由输入空间映射到特征空间，这样就把相应的预测问题转化优化的问题.

LSSVM的目标优化函数为

约束条件为

建立Lagrange函数

式（10）～（12）中：ε为指数；a为拉格朗日乘子；γ为正则化参数.根据最优化条件对L（w，b，ε，a）进行求偏导并消去εi和w后，把优化问题转化为求解下列线性方程组，即

式（13）中：Y＝［y1，y2，…，yl］T；α＝［a1，a2，…，al］T；Γ＝［1，1，…，1］T；I为单位阵；Ω可表示为

式（14）中：K（·）为满足Mercer条件的核函数.以最小二乘法求解系数ai和偏差b，可得混沌时间序列的LSSVM预测模型为

式（15）中：σ为径向基宽度是一个待定参数.

2.2 PSO参数寻优

PSO算法［11］起源于对鸟群捕食行为的研究，是一种模拟群体智能行为的优化算法.其基本原理是：每一次迭代，粒子通过跟踪个体极值Pbest和全局极值gbest这2个极值来更新自己的速度和位置；之后根据目标值的大小选择最优参数再次进行训练，直到得到目标训练模型.在找到2个最优解时，粒子根据下式来更新自己的速度和位置，即

式（16），（17）中：ω是惯性权重因子；v为粒子速度；χ为当前粒子位置；r1，r2为介于（0，1）之间的随机数；C1，C2为学习因子，通常取1.5.

LSSVM模型正则化参数γ和径向基宽度σ的选取对预测精度有很大的影响［12］.文中采用PSO算法来优化LSSVM参数.基本步骤如下：1）随机产生一组｛γ，σ｝作为粒子的初始位置，读取样本数据；2）进行LSSVM训练，计算训练样本的均方误差作为验证误差；3）以验证误差作为适应值，同时记忆个体与群体对应的最佳适应值的位置，再根据PSO优化方程搜索更好的｛γ，σ｝；4）重复训练与计算误差直到满足结束条件.

3 仿真研究

把一维Logistic系统、二维Henon系统和三维Lorenz系统3种典型的混沌系统作为研究对象.通过迭代计算得到混沌时间序列，均去掉前3 000个暂态数据，选取后3 000点作为实验数据，对所选数据进行归一化处理，选取合适的延迟时间和嵌入维数，对3种典型的混沌时间序列进行相空间重构.选用其中1 500个作为训练数据，应用相应的测试模型进行学习和预测，后1 500个作为测试数据.在PSO优化模型［13］中，采用的粒子种群数为20，最大迭代次数90，惯性权重为0.9.运行PSO优化模型，不断更新粒子当前的最优位置，分别得到3种混沌时间序列的LSSVM最优参数｛γ，σ｝，结果如表1所示.

为了衡量预测模型的有效性和精确度，采用均方误差（RMSE）作为评价整体预测性能的指标，即

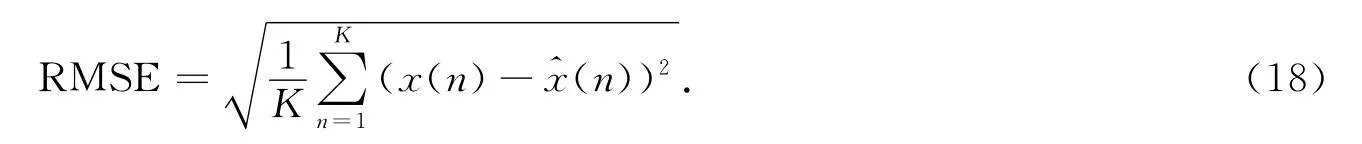
式（18）中：x（n）是第n个时间序列的实际值；＾x（n）是预测值.

应用LSSVM预测模型分别对3种典型混沌系统进行预测，表达式与预测结果如下所示.

1）考虑Logistic映射迭代表达式为

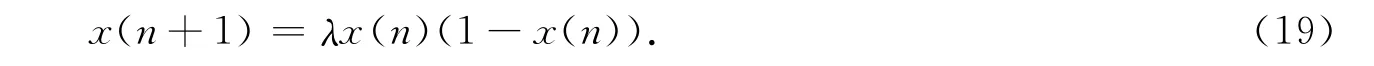
式（19）中：初始值取0.4，当λ＝4时，系统处于混沌状态.运用LSSVM预测模型的输出值和真实值的比较（x（n））和预测误差（e），如图1（a）所示.为了便于观察，图1（a），（b）只截取800到950之间的数据预测结果进行展示；图1（c）则截取800到900之间的数据.

2）考虑Henon映射迭代表达式

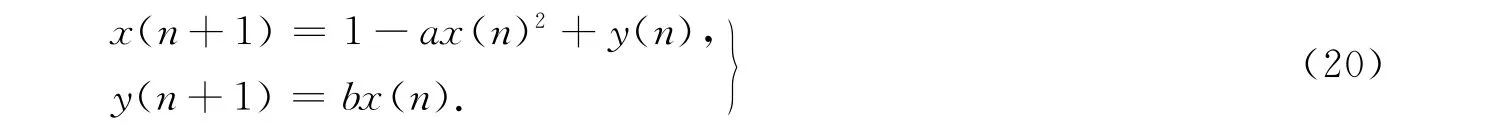
式（20）中：取a＝1.4，b＝0.3，此时系统处于混沌状态.预测结果如图1（b）所示.

3）考虑Lorenz映射迭代表达式

式（21）中：当s＝16，b＝4，r＝45.92时，系统处于混沌状态.运用LSSVM预测模型的输出值和真实值的比较和预测误差，如图1（c）所示.由输出误差可知：PSO优化的LSSVM模型能够实现对混沌时间序列较精确的预测.

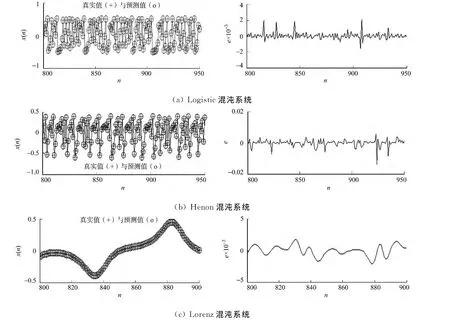
图1 不同混沌系统的预测结果Fig.1 Prediction results of different chaotic system

仿真实验中所用的参数，如表1所示.通过计算均方误差（＾e）作为衡量性能的标准，并与RBF神经网络建立的预测模型的预测结果进行比较.其中：RBF神经网络采用的是二层结构网络，神经元数目等于输入向量的个数，比较结果如表2所示.由表2可知：采用PSO算法优化的LSSVM的预测效果明显优于RBF预测算法.

表2 均方误差的对比结果Tab.2 Compared results of the mean square error

4 结束语

结合相空间重构理论建立LSSVM预测模型，利用PSO算法的全局优化和快速收敛的能力，克服了LSSVM预测模型参数选取的随机性，提高了LSSVM预测模型的泛化能力和预测精度.通过对3种典型的混沌时间序列进行预测，并与RBF神经网络建立的预测模型的预测结果进行比较，表明PSO优化的LSSVM预测模型的预测精度更高.

［1］ 党建亮.基于支持向量机的混沌序列预测方法研究［D］.成都：西南交通大学，2006：12-24.

［2］ 雷绍兰，孙才新，周浪，等.基于改进加权一阶局域预测模型的短期负荷预测方法研究［J］.电测与仪表，2006，43（455）：5-6.

［3］ CAO Liang-yue.Practical method for determining the minimum embedding dimension of a scalar time series［J］.Physica D：Nonlinear Phenomena，1997，110（1）：43-50.

［4］ 朱光兆，何伟.基于支持向量机的混沌时间序列预测分析［J］.自动化仪器仪表，2012（1）：145-149.

［5］ 往永生，刘卫华，杨利斌，等.基于最小二乘支持向量回归的混沌时间序列预测研究［J］.海军航空工程学院学报，2009，24（3）：283-288.

［6］ 翟永杰，王子杰，黄宝还，等.基于PSO优化的SMO算法研究及应用［J］.华北电力大学学报，2008，35（1）：57-61.

［7］ 孙涛，李健，郑豫，等.基于神经网络的混沌时间序列预测［J］.成都信息工程学院学报，2008，23（2）：126-130.

［8］ 张弦，王宏力.嵌入维数自适应最小二乘支持向量机状态时间序列预测方法［J］.航空学报，2007，31（12）：672-675.

［9］ 张淑清，贾键，高敏，等.混沌时间序列重构相空间参数选取研究［J］.物理学报，2010，59（3）：1576-1582.

［10］ 王朝.基于SVM的混沌时间序列预测方法研究［D］.保定：河北大学，2012：15-20.

［11］ 陈旭，刘延泉，葛建宏.基于PSO优化的LS-SVM 的混沌时间序列预测［J］.仪器仪表用户，2009，16（1）：135-136.

［12］ 孙斌，姚海涛.基于PSO优化LSSVM 的短期风速预测［J］.电力系统保护与控制，2012，40（5）：85-89.

［13］ 朱小明，张慧斌.PSO算法的稳定性分析及算法改进［J］.计算机科学，2013，40（3）：275-278.