柴油机气缸盖结构参数多目标优化*

盖洪武，程 颖，姚秀功

(北京理工大学机械与车辆学院，北京 100081)

前言

气缸盖是组成发动机最重要的零部件之一。近年来随着柴油机功率密度不断提高，气缸盖所面临的考验越来越严峻。其可靠性寿命已成为衡量发动机耐久性的重要指标之一［1－2］。不规则的几何结构、复杂的载荷加之材料不能满足要求，导致气缸盖容易发生疲劳破坏。因此要提高缸盖寿命就需要从以上3方面入手。然而，载荷方面，机械负荷由发动机性能决定，基本上固定;对缸盖结构强度影响最大的热负荷很大程度上受结构影响;材料方面，缸盖材料一般在铸铝和铸铁之间选择，新材料研究工作进展缓慢，并无新材料问世。所以通过优化结构提高缸盖寿命是最有效可行的方法。

由于气缸盖在高温高压环境下工作，应力实测非常困难并且费用昂贵。为了降低成本、缩短缸盖设计周期，目前普遍采用有限元仿真分析计算气缸盖的结构强度。一些有限元软件已经能够联合三维建模软件自动进行多目标优化设计，前提是研究对象能够参数化建模。然而对于复杂的缸盖而言，一个或少量结构特征的参数化是可实现的，但缸盖整体模型参数化非常困难。本文中从降低多个气缸盖疲劳危险部位应力水平的角度着手，综合运用正交实验法、方差分析、二次响应面回归和遗传算法，对缸盖结构参数进行了敏度分析和多目标优化。

1 有限元计算

1.1 气缸盖简化模型

为便于规律性的研究，采用简化的气缸盖几何模型进行研究。参考样机为某V型8缸柴油机，缸径为132mm，额定转速为2 500r/min，单缸功率为92kW。原气缸盖为单体式结构，四气门，喷油器垂直中置，一个螺旋进气道，其余气道均为直气道。简化缸盖保留了原型机的总体外廓参数、紧固螺栓个数与直径及位置、进排气门直径及位置、进气道进口面积、排气道出口面积、进排气道位置、喷油器位置。在此基础上简化处理了气缸盖顶部结构、水套(底板侧除外)和不影响结构强度的工艺结构。简化模型保持了主要承载体系不变，因此进行简化是可行的。本文中研究的12个结构参数为参数化设计的。简化缸盖几何模型如图1所示。

1.2 有限元模型

为保证计算精度，将简化缸盖与缸垫、缸套和机体装配在一起进行计算。简化模型为对称结构，为降低网格规模，取1/2模型进行分析研究。具体描述如下:

(1)气缸盖、机体、缸垫、缸套均采用四面体二次单元划分网格，缸盖全局网格种子4mm，对疲劳危险部位进行局部网格加密，局部种子大小2mm，螺栓用梁单元模拟;

(2)材料属性定义为弹塑性，缸盖材料为HT250;

(3)分析类型为稳态分析;

(4)缸盖与缸垫之间、机体与缸垫之间接触定义为小滑移。

1.3 边界条件

计算温度分布时采用第三类热边界条件，即给出加热表面和散热表面处介质(燃气、冷却水)的温度和换热系数。由GT-Power软件的性能仿真分析得到的瞬时燃气换热系数和温度，分别求得一个循环的燃气加权平均换热系数为1 519.9W/(m2·K)，加权平均温度为731℃。冷却水温度由原型机实际测得为85℃，将冷却水的平均换热系数设置为4 000W/(m2·K)［3］。通过试验测得的进排气、缸内压力和喷油量等数据，设置模型参数，并通过试验结果校核模型计算结果，最终得到进气、排气和燃气等边界条件，为气缸盖的稳态热分析计算提供数据条件。在与紧固螺栓、气门座圈、气门导管(均布载荷模拟)、机体装配条件下，叠加气缸盖温度场，进行热机耦合仿真分析，详细方法参见文献［3］。

2 正交实验设计

缸盖结构形式复杂，结构参数繁多。选取火力板厚度、鼻梁区宽度等12个参数进行研究，每个参数在许用范围内取3个水平。利用有限元软件Abaqus进行热机耦合计算得到缸盖疲劳危险部位的应力计算结果。如若每个参数改变一次则进行一次计算，则共需312次仿真计算，其工作量惊人。为了降低计算成本，采用实验设计中广泛应用的正交设计法，挑选出部分代表性很强的参数组合来仿真。这些组合具有整齐可比性、均衡分散的特点。在保证分析结果准确性的同时极大降低了计算次数，提高了工作效率［4］。

2.1 因素及目标

为了不遗漏重要的结构参数，在初期研究参数的范围应尽可能广。共选取12个可能会影响疲劳危险部位受力状况的结构参数作为考察因素:火力板厚度(x1)、鼻梁区宽度(x2)、气门导管孔座壁厚(x3)、气门座圈镗孔深度(x4)、气门锥角(x5)、喷油孔长度(x6)、喷油器护套厚度(x7)、喷油孔直径(x8)、气门导管与顶板过渡圆角(x9)、顶板厚度(x10)、气道与底板过渡圆角(x11)、侧墙厚度(x12)。每个因素取3水平，如表1所示。

结构参数中取中间水平时对应的值即为原型机结构尺寸。为了研究结构参数对应力分布的影响规律，分别在原尺寸上下各取一个水平作为研究范围。在选取范围时充分考虑了具体结构之间的相互关系(保证不发生干涉，尽量保持各参数的独立性和各次实验中整体模型的一致性)并参考了设计手册中的经验范围。

选择3个缸盖疲劳危险部位等效应力值为目标值。3个部位分别为:排气门鼻梁区(y1)、进排气门鼻梁区(y2)和气门座圈镗孔(y3)，如图2(b)所示)。

2.2 正交表选用

此次计算为12因素3水平，不考虑因素的交互作用。选择L27(313)表，因为它是可以容纳12因素所需仿真次数最少的正交表，共需要27次有限元仿真计算。恰好留有一个空列，以便于方差分析。结合因素和水平表即可得到实验方案。实验方案和仿真分析结果见表1。因为实验次数较多，仅将正交实验中1号计算的温度分布云图和热机耦合等效应力分布云图作为示意，如图2所示。

表1 实验方案及仿真结果

3 敏度分析及参数筛选

对正交实验的结果进行方差分析。因素的偏差平方和反映了水平变化对响应值引起的波动，e为计算误差引起的响应值波动。如果因素偏差平方和小于误差平方和，则认为因素水平变化对响应值的影响可以忽略［4］。定义贡献度为因素偏差平方占总偏差平方和T的比值［5］，比较贡献度大小可以直观得到评价目标值对各参数的敏感程度。

取显著性水平0.1和0.01，查F分布临界值表可知 F0.1(2，2)=9，F0.01(2，2)=99。当 F 大于 F0.01(2，2)=99时，称因素高度显著，记为＊＊;若值小于 F0.01(2，2)大于 F0.1(2，2)时，称因素显著，记为*;当F小于F0.1(2，2)时，称因素不显著。

将所得结果按贡献度降序排列，全部分析结果见表2～表4。

表2 y1方差分析表

由分析结果知，y1的显著因素有3个(x1、x4、x10);y2的显著因素有 4 个(x1、x12、x4、x3);y3的显著因素同样为4个(x4、x1、x2、x12)。显著因素影响要远远大于不显著因素，y1－y3的显著因素贡献度之和高达91.5%、95.6%和97.5%。不显著因素作用对响应值波动影响很小，可以忽略。因此选择显著性为判定标准筛选因子是合理的。筛选出6个重要的结构参数分别为:x1、x2、x3、x4、x10、x12，这样在缸盖众多结构参数设计过程中就能够有的放矢，不必浪费精力在一些影响微小的参数上，为后续的多目标优化缩小了范围。

表3 y2方差分析表

表4 y3方差分析表

4 多目标优化

4.1 构建回归方程

响应面模型是代理模型的一种，是一种高效的近似求解方法。响应面法通过选取设计空间内一定数量的设计点来构造响应函数作为近似数［6］。二次多项式回归与响应面分析相结合的研究方法范式叫做二次响应面回归方法。本文中选择具有较高准确性的二阶多项式响应面模型，构造y1－y3的响应面回归方程表达式如下:

因为是近似求解，样本点和多项式基函数的选择都会给方程的拟合结果造成一定的误差。用复相关系数R2来评价响应面模型对试验数据的拟合精度。其值越接近1，说明误差的影响越小，则响应面的精度越高。拟合的3个目标函数复相关系数分别为0.923、0.956、0.971，表明所建立的模型可以用来解释92.3%、95.6%、97.1%的响应变化，精度满足工程要求。

4.2 多目标优化

多目标优化问题不存在唯一的全局最优解，而是各个目标在不同权重系数下组合的一系列解的集合，为多目标优化问题的Pareto最优解集，也称为非劣解或非支配解。Pareto最优解中任何一个目标函数的值在不使其他目标函数值恶化的条件下已不可能进一步优化［7］。另外，Pareto最优解集中的每一个解仅仅是多目标优化问题的一个可以接受的非劣解，对于大多数的工程实际问题而言，在求得多目标优化问题的Pareto解集后，要根据工程实际问题的期望值或目标值，从众多最优解集合中选择合适的一个或者多个解作为问题的最终解。

运用MATLAB优化工具箱中基于遗传算法的多目标优化，结合编程。求3个目标函数同时较小的值以及此时的参数值，设定6个因素的水平的上下界为约束条件。最终所得的Pareto解集中包含32组解。对于缸盖疲劳危险部位而言，期望y1－y3越小越好。因此以 y1＜170MPa，y1＜170MPa，y3＜150MPa为限定条件，对Pareto解集进行筛选。优选出的Pareto非劣解集见表5。

表5 多目标优化Pareto非劣解集

4.3 验证最优解

4个Pareto非劣解中，1号解y2值最小，但是y1值最大;2号解y1值最小，但是y3值最大;3号解y3值最小，但是值y2最大。本文中多目标优化目的是让3个响应值同时降低，而不是以提高一个响应值的代价来降低另一个响应值。4号Pareto非劣解中，3个响应值均不是最优的，但却都是较优的。综合考虑选定4号解为最优解。对其进行仿真验证，对比结果见表6。响应值的优化解与仿真结构误差均不超过5%，能够满足工程设计的需要，同时也验证了回归方程的精确性和优化结果的正确性。

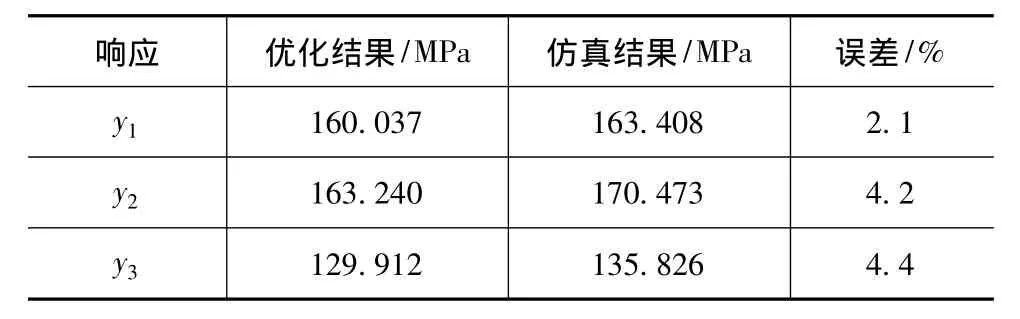
表6 优化结果与仿真分析对比

5 结论

综合运用正交设计、响应面回归和多目标优化的方法，得到了缸盖疲劳危险区域应力值受12个结构参数影响的敏感程度，发现火力板厚度、鼻梁区宽、座圈镗孔深、导管壁厚、顶板厚度和侧墙厚度是响应值的显著因素，其重要程度远远高于其余因素。构建了具有较高精度的响应值的二次响应面回归方程，采用遗传算法多目标优化得到了最优结构参数组合方案，并通过了仿真验证。相比27次正交实验的平均值，优化后的排气门鼻梁区、进排气门鼻梁区和气门座圈镗孔等效应力值分别降低了11.3%，19.7%，15.7%，取得了良好的优化效果。本文中研究为柴油机气缸盖优化设计提供了参考思路。

［1］ Gocmez T，Pischinger S．A Contribution to the Understanding of Thermomechanical Fatigue Sensitivities in Combustion Engine Cylinder Heads［J］．Journal of Automobile Engineering，2011，225(4):461－477．

［2］ Martin Riedler，Heinz Leitner，Bernd Prillhofer，et al．Lifetime Simulation of Thermo-mechanically Loaded Components［J］．Meccanica，2007(42):47 －59．

［3］ 赵维茂．柴油机铸铁气缸盖的热疲劳裂纹演化规律与寿命评估研究［D］．北京:北京理工大学，2011．

［4］ 赵选民．实验设计方法［M］．北京:科学出版社，2009:66－114．

［5］ Pamela Marie Norris．An Investigation of Coolant Passage Heat Transfer in a Diesel Engine Cylinder Head［D］．Atlanta:Georgia Institute of Technology，1992．

［6］ 兰凤崇，钟阳，庄良飘．基于自适应响应面法的车身前部吸能部件优化［J］．汽车工程，2010，32(5):404 －408．

［7］ Shyy W，Papila N，Vaidyanathan，et al．Global Design Optimization for Aerodynamics and Rocket Propulsion Components［J］．Progress in Aerospace Sciences，2001，37(1):99 －118．