燃气轮机故障诊断中的基准参数计算
2014-10-10林满山郭永辉
林满山 郭永辉
(北方工业大学信息工程学院,北京100043)
0 引言
在燃气轮机的故障诊断中,热力参数的变化量往往可以用来计算燃气轮机发生故障时的性能变化、判断故障产生的原因。为了计算热力参数的变化量,首先需要准确获得足够的燃气轮机无故障状态下的热力参数。为了建立燃气轮机基准模型,目前主要通过大量实验数据建立燃机仿真模型[1-2],或者由厂家提供的部件特性曲线和测试数据获得基准模型的性能参数[3],也可通过推导气动热力学方程获得数学计算模型[4-5]。然而在实验成本高昂、发表数据可靠性不强、热力学方程的推导结果精度往往不够的情况下,如何综合使用各种方法,以最小的成本获得尽可能准确和足够的性能参数在燃气轮机故障诊断中有着重要的意义。
本文提出了应用机器学习中的支持向量机理论[6-8],利用其处理小样本数据时学习能力强的优势对有限的燃气轮机基准运行数据进行学习,从而建立起基准参数计算模型。以某三轴燃气轮机为例,对文献[9]中的实际数据进行了建模,结果表明该方法具有很好的适用性。
1 回归型支持向量机
支持向量机(SV M)是建立在统计学习理论基础上的一种新的通用学习方法。统计学习理论采用结构风险最小化准则,在最小化样本点误差的同时,最小化结构风险以提高泛化能力,且突破了维数的限制。利用支持向量寻求最优分类面,其主要思想是建立一个分类超平面作为决策曲面,使得正例和反例之间的隔离边缘最大化。
根据相关理论,当SV M用于回归预测时就是寻找一个最优分类面使得所有训练样本离该分类面的误差最小。设训练集含有N个训练样本{(x→i,yi),i=1,2,…N},其中,x→i是第i个输入向量,yi为对应的输出值。
设要建立的线性回归函数为:

定义ε线性不敏感损失函数:
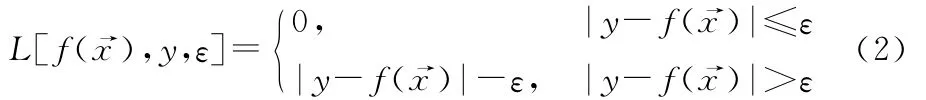
燃气轮机气动部分的故障诊断主要是通过压气机和透平的性能参数(如流量、效率)变化来判断故障类型、位置,而实际运行中往往不能直接监测到这些性能参数。这种情况下,就需要建立起可测参数与性能参数之间的关系,通过可测参数得到所需的性能参数。然而燃气轮机作为一种复杂的先进热力设备,其热力参数之间的关系也是高度非线性的,通常的做法是用半经验公式或非线性多项式进行拟合,通过这些关系式可以得到不同工况下机组的性能参数。虽然这些方法在分析燃气轮机部件性能、拟合特性曲线方面有一定的适用性,但对特定机组的性能参数进行计算时,其往往需要大量数据才能达到一定的计算精度,因而在燃气轮机实验代价及精度要求高的条件下,这些方法略显局限性。
支持向量机是针对小样本数据处理提出来的一种新型智能学习算法,对于较少样本的情况学习能力比较强。本文提出在燃气轮机基准参数的计算中可利用支持向量机计算所需的性能参数。其基本思路是将影响性能参数的可测参数作为SVM模型的输入向量,将要求的性能参数作为输出向量,利用数据样本对SV M模型进行训练,得到可用的模型用于燃气轮机基准参数计算。
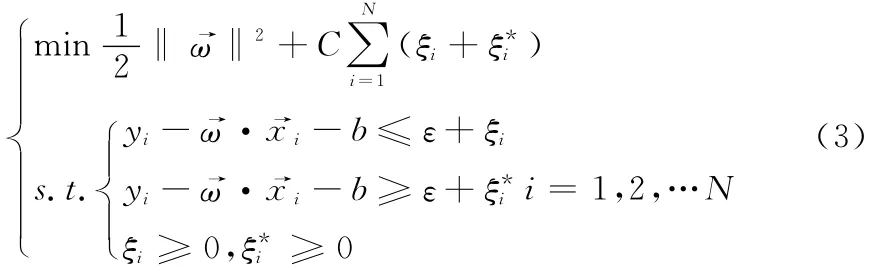
其中,ε规定了回归函数的精度要求;C为惩罚因子,C越大对训练误差大于ε的样本的惩罚就越大;ξi为松弛变量的上下限,受惩罚因子C的压制。
实践中问题往往是非线性的,简单的分类面无法达到要求,这时需通过非线性映射φ)将原来输入空间的样本映射到高维特征空间中,然后在此空间中构造最优分类超平面。定义核函数K()=φ()φ(),以代替原最优分类面中的点积。按照优化理论中的Kuhn-Tucker定理,通过KKT互补条件很容易求解上述拉格朗日函数的对偶问题。支持向量机在建模上表现出很多优势:针对小样本,在样本有限的情况下能获得最优解;算法最终转化为二次规划,理论上可以避免陷入局部最优;良好的泛化能力;能解决“维数灾”问题。由于其优异的性能,SV M在各领域得到了广泛的应用。
2 燃气轮机基准参数计算
以压气机流量计算为例,具体方法如下:(1)构建数据样本。采集一定量的压气机热力参数样本从中得到所需的压比、折合转速、折合流量等数据。以压比、折合转速为样本集输入变量,折合流量为输出变量。(2)数据归一化处理。即将数据输入基准化到统一的量纲范围里,这样可以避免过大的绝对值输出误差的影响,使训练模拟的范围相对集中,提高模型计算性能。(3)训练支持向量机回归拟合模型。根据支持向量机的基本理论,构建回归拟合模型需选择合适的核函数以及参数组合。支持向量机的核函数有很多,本文采取径向基(RBF)核函数此核函数预测精度比较好。设定精度ε的值后,利用交叉验证的方法寻找惩罚因子C和核函数中方差σ的最佳组合。用数据样本对支持向量机进行训练,得到可用的支持向量机模型。(4)模型计算。利用得到的SVM模型,输入一定的压比、折合转速,便可得到相应模型计算所得的折合流量。同理,利用这种建模方法可建立压气机效率、透平流量、透平效率等性能参数的计算模型,进而得到所需的各种工况下的基准性能参数。
3 仿真模拟
以某型三轴燃气轮机的压气机部分为例对上述方法进行验证,在Matlab平台下利用文献[9]中的实验数据建立支持向量机模型,计算基准状况下压气机流量和效率性能参数。
首先建立压气机折合流量模型。对数据进行筛选,得到8组数据用来构建样本集,其中压比和折合转速为输入样本集,折合流量为输出样本集。设定精度ε=10-4,利用交叉验证的方法得到最优参数组合为C=724.08,σ=32。训练SV M回归拟合模型,将样本中的8组数据中输入变量回代到训练所得SV M模型中,可输出相应的折合流量值。模型计算值与实验值比较如图1所示,最大相对误差0.711%,平均相对误差0.401%,与文献中最大相对误差1.06%和平均相对误差0.323%的结果相当。
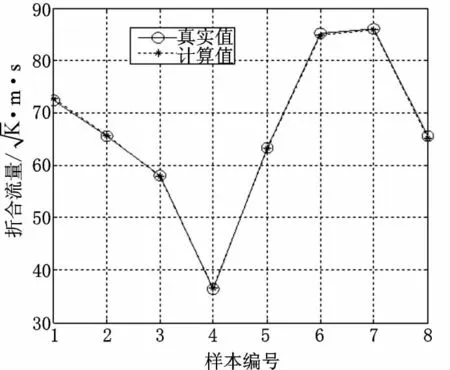
图1 压气机折合流量计算结果
同理,按照前述方法对压气机效率进行建模,设定精度ε=10-4,优化得到参数组合为C=512,σ=32,得到的压气机效率模型计算结果与实验结果对比如图2所示,最大相对误差0.221%,平均相对误差0.061%,低于文献中最大相对误差1.17%和平均相对误差0.412%的精度。
从计算结果可以看出,此方法精度较高,利用该模型能很好地对燃气轮机基准参数进行计算。

图2 压气机效率计算结果
4 结语
针对燃气轮机故障诊断中基准参数的计算问题,本文提出了利用支持向量机理论建立无故障状态下基准参数计算模型的方法。结合故障诊断中通过可测参数获得性能参数的研究思路,提出了建立基于支持向量机的基准参数一般计算模型的步骤,通过Matlab实现了模型的软件计算,表明该方法可实现动态计算。利用支持向量机处理小样本时学习能力强的特点,该支持向量机模型能利用有限的实验数据进行建模,有利于减少实验成本。在利用已有文献实验数据的仿真模拟中,该支持向量机模型的计算误差均在1%以内,这表明模型具有很高的计算精度,能有效地计算燃气轮机基准性能参数,对进一步研究燃气轮机性能、进行故障诊断有着重要的价值和意义。
[1]杨欣毅,刘海峰,董可海.依据试验数据求取航空发动机部件特性的新方法[J].航空计算技术,2009(3):48~55
[2]黄晓光,王永泓,翁史烈.燃气轮机混合智能故障诊断专家系统[J].船舶工程,2000(6):37~39
[3]于美玲,刘永文.基于非线性模型的燃气轮机热参数故障诊断及仿真[J].热能能动力工程,2011(6):651~654
[4]杨欣毅,刘剑锋,张强,等.粒子群优化算法求解航空发动机模型的应用[J].航空计算技术,2007(6):39~44
[5]吕泽华,黄志明.三轴燃气轮机变工况小偏差范围内的解析解[J].燃气轮机技术,1995(2):31~38
[6]徐玉兵.支持向量机在道路交通事故预测中的应用[J].交通标准化,2010(1):160~162
[7]Keerthi S,Lin C J.Asy mptotic behaviors of support vector machines with Gaussian ker nel[J].Neural Computation,2003(7):1 667~1 689
[8]王春林,周昊,李国能,等.基于支持向量机与遗传算法的灰熔点预测[J].2007(8):11~15
[9]蒋磊,杨朔.基于Matlab的燃气轮机热参数故障诊断的标准数学模型建立[J].科学技术与工程,2009(5):1 254~1 257
