基于不同假设的权益联结型年金的准备金研究
2014-10-10王学金魏佳丽
李 衍,王学金,魏佳丽
基于不同假设的权益联结型年金的准备金研究
李 衍,王学金,魏佳丽
准备金的提留是研究寿险产品的一个重要课题,以权益联结型年金产品中的最低期满利益保证年金为研究对象,假定标的权益服从一个随机波动性模型,得到了最低期满利益保证年金在 分位数下的准备金的显式表达式,然后在其基础上分别研究了嵌入动态提款权的最低保证收益型年金和考虑死亡风险的最低保证收益型年金的准备金,并以 2012年深成指日交易收盘价数据为样本对对数收益率进行了基本统计分析,最后对三种不同权益联结型年金的准备金进行了比较分析。
随机波动模型;最低期满利益保证年金;动态提款权;死亡风险;分位数准备金
近年来,随着收入水平的提高,投资者的投资需求不断增加,保险市场上的一些传统理财产品已经无法满足投资者的投资需求,于是各种新型的年金产品应运而生,权益联结型年金就是其中的一种。权益联结型年金产品的定价问题近年来已被国内外学者们做了相当充分的研究,仅以EIA为例,Serena Tiong[1]通过 Esscher 变换给出了传统的 EIA的定价公式;Imai 和 Boyle[2]提出了动态最低保证收益率,并在最低保证收益率是变化的情况下得到了EIA的定价公式;Virginia R.Young[3]通过均衡效用理论讨论了 EIA 的定价问题;王学金和王传玉[4]在假定死亡率带跳情形下,得到对应的 EIA的定价公式,并将其与经典Lee-Carter死亡率模型下的结果进行了比较分析。同样地,近年来关于权益联结型年金产品的准备金提留的研究也开始流行起来,如王学金和王传玉[5]研究了基本的权益联结型年金的准备金,因此,本文主要是在王学金和王传玉[5]的基础上着重研究基于不同假设的权益联结型年金产品的准备金提留问题。
考虑到标的权益的增长过程本质上是一种无规律的随机波动,而波动性的测度方法主要有随机波动模型(SV模型),其特点是以参数求解为基础,模型不存在确定的函数表达式。国内外学者对于该模型进行了许多相关研究,如 Harvey A et al[6],Jacquier et al[7]和沈根祥[8]等的研究结果表明:在模拟股市的波动性时,SV模型较一般随机模型如GARCH模型更加具有优势。因此本文主要基于随机波动模型来研究权益联结型年金的准备金提留问题,即本文假定标的权益的价格过程服从标准的SV模型,求出三种权益联结型年金在 分位数下的准备金的显式表达式,然后通过实证数据对三种模型进行比较分析,并对结果进行实际意义解释。
1 标准的SV模型
标准的SV模型是Taylor为了解释金融收益序列波动模型的自回归行为而提出的,其标准形式如下[9]:
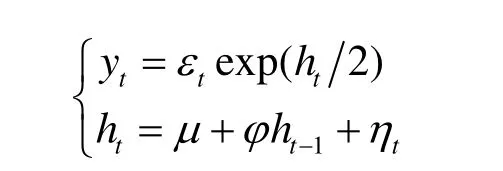
其中yt表示t时的收益率;εt~nid(0,1),ηt~nid(0,t2)(nid表示正态独立同分布);误差项ηt和εt是相互独立的且不可测的;μ,φ是常数且当时,SV模型是协方差平稳的;隐波动ht服从参数为φ的高斯AR(1)过程。
2 权益联结型年金的 分位数准备金
权益联结型年金的准备金研究就是比较年金到期权益积累值和最低保证收益积累值的大小问题,即:若前者大于后者,则无需提留准备金;若前者小于后者,则需提留准备金。为了保证自身的偿付能力,保险公司一般会将年金的到期权益积累值与准备金积累值之和大于最低保证收益积累值的概率控制在一定的范围内。
为了计算年金的 分位数准备金,我们假定年金的标的权益的价格过程rt服从标准SV模型,具体形式如下[3]:
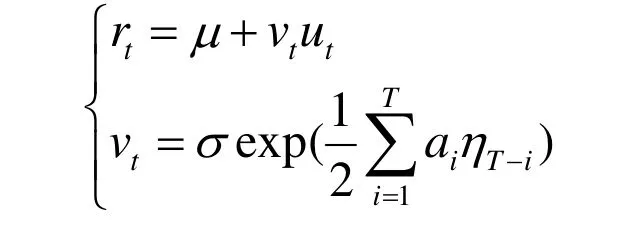

2.1 最低保证收益型年金
最低保证收益型年金(GMMBA)一般有最小收益的保证, 在最小保证收益的基础上年金实际支付给保户的收益率与预先规定好的某类股票指数或债券指数收益相关联,此类年金的典型代表有权益指数年金。对于此类年金的准备金的研究,我们有:
定理1[3]记 表示最低保证收益率,P表示趸缴保费,St表示t时标的权益的价格,F(t)表示t时账户的现值,m表示管理费率,T表示权益联结型年金的到期日,rt表示t时的对数收益率,Vα表示损失分布的 分位数准备金, 表示保险公司无损失风险的概率,则

2.2 附动态提款权的最低保证收益型年金
附动态提款权的最低保证收益型年金(GMMBA-DDR)是在最低保证收益型年金的基础上进行了优化,给年金购买者提供了一项权利:动态提款权,即若在年金有效期间内,年金购买者因为某种突发因素急需现金,则保险公司可以给予购买者提供提现的条件,类似于银行定期存款一样。对于此类年金的准备金的研究,我们有:
定理 2记λt表示t时保单持有人从账户中的提款率,其余符号含义同定理1,则
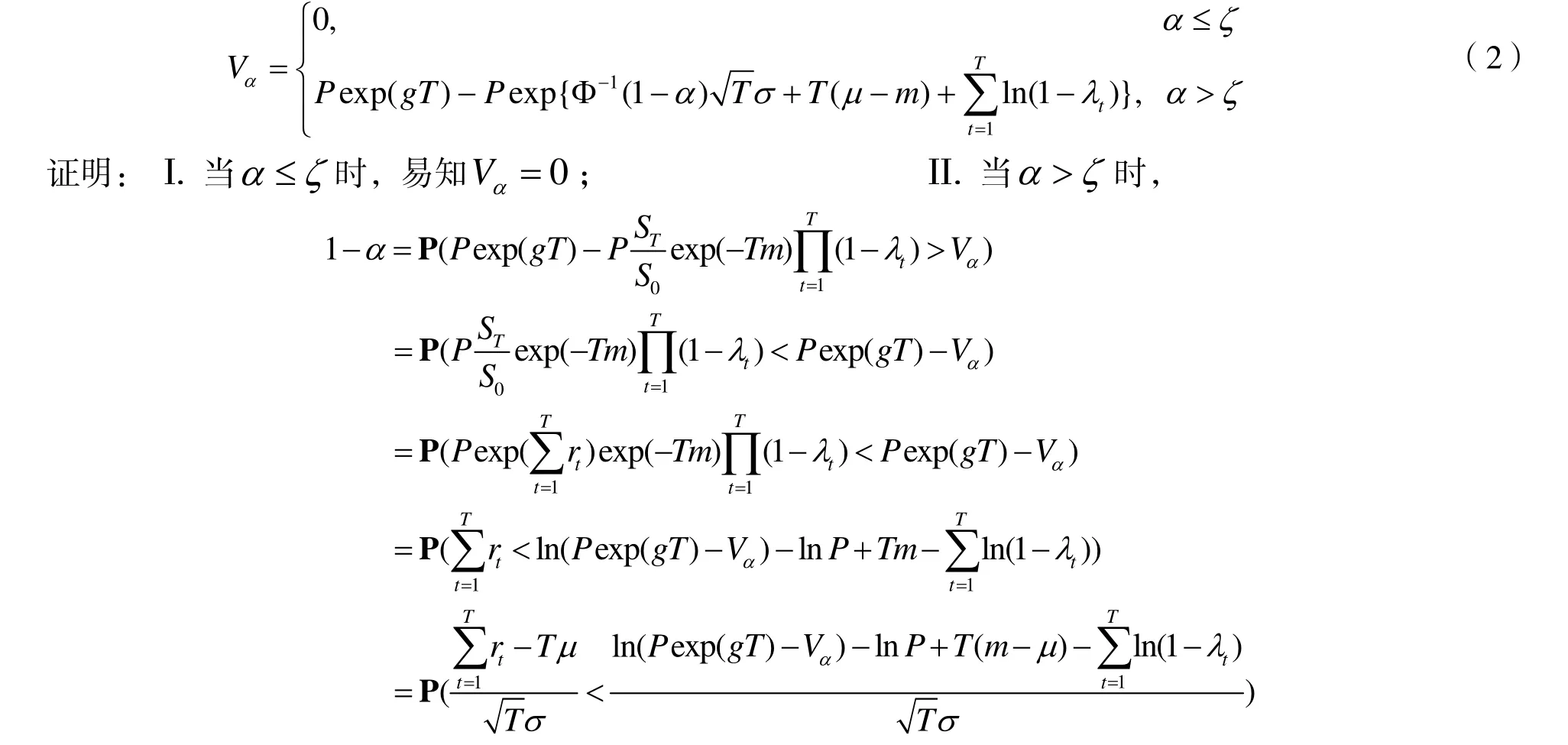
由中心极限定理可知,当T充分大时,有

故当T→∞时

推论在定理2的条件下,当各个周期内保单持有人从账户中的提款率相同,即当
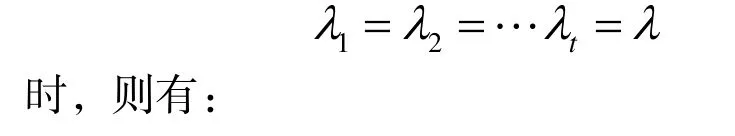
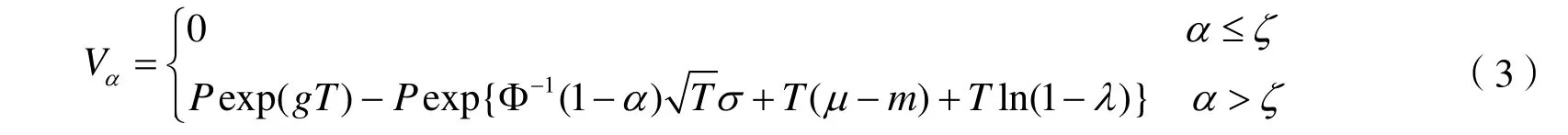
注:当λ=0时,我们则可得到一般的最低保证收益型年金的准备金的表达式,即定理1。
2.3 考虑死亡风险的最低保证收益型年金
考虑死亡风险的最低保证收益型年金(GMMBA-MR)是在最低保证收益型年金的基础上直接外加一个死亡风险因子tpx,即 岁个体活过t年的概率。因为随着社会经济水平的提高和医疗卫生条件的改善,我国的人口死亡率整体呈现逐年下降的趋势,而时间变动带来的不确定性却未能在最低保证收益型年金(GMMBA)和附动态提款权的最低保证收益型年金(GMMBA-DDR)的准备金提留中准确地反映出来,从长期来看,保险公司的经营将面临巨大风险,所以在此我们对此类年金的准备金进行研究,可得:
定理 3记tpx表示 岁个体活过t年的概率,其余符号含义同定理1,则

3 实证分析
3.1 对数收益率的统计分析
考虑到样本数据和样本区间的不同,会对波动性特征的刻画以及模型估计的结果产生较大影响,并且股票市场的波动性也会随时间的变化而变化,因此,为了能够较为准确地研究我国股票市场的波动特征,在样本数据方面,本文选用最近的2012年全年深证成指日交易收盘价(共239个交易数据)来对对数收益率序列{rt}进行研究,数据来源于wind资讯。
基于选择的样本数据,对其进行基本的统计特征分析,可得基本统计变量的估计值,见表1。
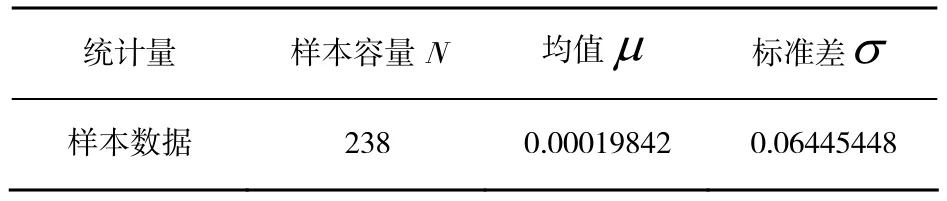
表1 深成指日交易数据序列描述性统计分析结果
3.2 分位数准备金的影响因子分析

表2 GMMBA和GMMBA-DDR对应的准备金比较分析

表3 GMMBA和GMMBA-MR对应的准备金比较分析
由表2易知,当α>ζ时,若固定最低保证利率g、到期日T和管理费率m,则 GMMBA和GMMBA-DDR对应的准备金Vα随着α的增加而增加;当其他影响因子不变时,准备金随着λ的增加而增加,因为λ的增加,表明保单持有人从账户中提款较多,这就影响了保险公司的财务管理,给财务管理带来了不确定性,相应地增加了保险公司的财务风险,因此导致准备金的增加。
为了对GMMBA和GMMBA-MR模型下的准备金进行比较分析,在对考虑死亡风险的权益联结型年金时,我们首先假定购买者的年龄为 岁,然后根据中国人寿保险业经验生命表(1990-1993)得到对应年龄下的人口数据lx,再根据公式tpx=lx+t/lx即可得到对应年龄下的死亡率,最后可得表3。
由表3易知,同表2一样,当α>ζ时,若固定最低保证利率g、到期日T和管理费率m,则GMMBA和GMMBA-MR对应的准备金Vα随着α的增加而增加;当其他影响因子不变时,准备金Vα随着T的增加而增加,因为T的增加,这是因为随着到期日的延长,
不确定性变大,保险公司的风险随之增加,同时考虑死亡风险因素时,未来的死亡率会随着年龄的增加(与T同向变化)而增加,因此在这双重因素的影响下,保险公司需要提留更多的准备金。
4 结论
本文主要研究了 SV模型下 GMMBA、GMMBA-DDR和GMMBA-MR的α分位数准备金的提留问题,基于一定的假设得到对应的显式表达式,并以2012年深成指日交易收盘价数据为样本对三类年金的准备金进行了比较分析,借此将基本权益联结型年金的准备金研究进行了推广,一定程度上解决了保险公司的权益联结型年金的准备金的提留问题。
[1] Tiong S. Valuing equity indexed annuities [J]. North American Actuarial Journal, 2000,4 (4):149-163.
[2] Imai J,Boyle P. Dynamic fund protection. North American Actuarial Journal[J].2001,5(3):31-49.
[3] Young V.R .Equity-indexed life insurance: pricing and reserving using the principle of equivalent utility[J].North American Actuarial Journal. 2003, 7(1):68-86.
[4] 王学金,王传玉.不同死亡率模型下基本权益指数年金定价的比较分析[J]. 吉林师范大学学报(自然科学版),2013,34(1): 100-102+107.
[5] 王学金,王传玉.随机波动性模型下权益联接型年金的准备金[J]. 南通大学学报(自然科学版),2013,12(3):78-81.
[6] Harvey A, Ruiz E, Shephard N. Multivariate stochastic variance models[J],Review of Economic Studies,1994(61):247-264.
[7] Jacquier E,Polson N.G, Rossi P.E. Bayesian analysis of stochastic volatility models[J],Journal of Business&Economic Statistics,1994,12(4):371-388.
[8] 沈根祥. 股票收益随机波动模型研究[J].中国管理科学,2003,2(11):16-20.
[9] Taylor S.T. Modeling financial time series[M],Wiley,New York,NY,1986.
[10]Hwai-Chung Ho et al. Evaluating Quantile Reserve for Equity-Linked Insurance in A Stochastic Volatility Model: Long VS. Short Memory[J], Astin bulletin,2010,40(2):669-698.
责任编辑:王与
O211.67
A
1673-1794(2014)05-0083-04
李衍,魏佳丽,滁州学院数学与金融学院; 通讯作者:王学金,滁州学院数学与金融学院教师,硕士(安徽 滁州 239000)。
全国大学生创新创业训练计划(2014CXXL005);安徽省级金融工程教学团队(2013jxtd035)
2014-05-12
