热采水平井塑性破坏半径预测方法及应用

李彦龙，董长银，李怀文，邵力飞，陈新安

(1.中国石油大学(华东)石油工程学院，山东青岛 266580； 2.中国石油大港油田公司石油工程研究院，天津300280)

热采水平井塑性破坏半径预测方法及应用

李彦龙1，董长银1，李怀文2，邵力飞2，陈新安1

(1.中国石油大学(华东)石油工程学院，山东青岛 266580； 2.中国石油大港油田公司石油工程研究院，天津300280)

有关疏松砂岩油藏水平井塑性破坏半径的研究没有考虑高温交变应力对近井岩石塑性破坏过程的影响.分析热采复杂条件下的水平井近井地层应力分布规律，提出基于不同岩石破坏准则的近井塑性破坏半径预测方法.结果表明，井壁处的塑性屈服函数值越大，井壁破坏程度越大，出砂越严重，塑性屈服函数的零点即为塑性破坏半径.井底温度越高，塑性破坏半径越大.塑性破坏半径受原地主应力顺序、井周角、方位角、井底流压等因素影响.当垂向主应力大于水平主应力时，垂直方向上的塑性破坏半径最大；反之，水平方向上的塑性破坏半径最大.当水平井方位角为0°(或180°)时，井周塑性破坏半径最大；当水平井方位角为90°(或270°)时，井周塑性破坏半径最小.该研究成果对于热采水平井出砂预测有一定的指导意义.

塑性破坏半径；出砂预测；热采；水平井；近井应力；出砂半径

0 引言

在我国疏松砂岩稠油油藏分布广泛，出砂是疏松砂岩油藏热采水平井生产所面临的主要问题之一.热采水平井出砂的实质是近井储层岩石在交变温度、交变应力作用下达到岩石塑性破坏条件而发生塑性破坏，在近井地带形成塑性破坏区，塑性破坏区内的离散砂在流体携带作用下进入井筒造成出砂.因此，对于已出砂的热采水平井，井底塑性破坏半径预测及井壁稳定性分析对于直观了解井底出砂状况，准确评价砂程度和采取针对性的防砂施工具有指导意义.目前，有关疏松砂岩油藏水平井井底塑性破坏半径的研究主要集中在常规开采条件下的水平井塑性出砂半径预测方面[1-6]，关于热采水平井近井塑性出砂半径的预测研究未见报道.由于受注入压力、注入温度和井壁渗透性等因素影响，近井地层应力随时间不断发生变化，因此热采条件下的塑性半径预测必须考虑高温、高压等条件的影响.

常规冷采井塑性破坏半径预测方法是首先将近井弹性变形区的应力表达式代入岩石破坏准则，推导塑性破坏半径以内的塑性应变方程；然后根据弹—塑性界面处应力连续分布原理，预测近井地层塑性破坏半径[2，7].该方法推导复杂且推导的塑性应变方程不适用于热采开发井，不具有通用性；也可以通过有限元法模拟建立近井塑性破坏半径计算方法，但复杂程度很高[8-10].笔者提出利用屈服函数判断井壁破坏程度及预测近井塑性破坏半径的方法，对模型进行算例分析及敏感性分析.

1 近井应力分布规律

稠油热采水平井开发过程中，复杂条件导致近井地层应力不断发生变化，当近井岩石承受的应力超过一定范围时，井眼周围的岩石开始屈服，在井壁周围形成一层塑性破坏圈，塑性破坏圈以外的岩石处于弹性状态，塑性破坏圈的外半径即为热采水平井的塑性破坏半径.以塑性破坏半径为界，将整个地层分为塑性破坏区和弹性变形区(见图1，其中rb为地层的塑性破坏半径，rw为井径，re为地层供油半径).

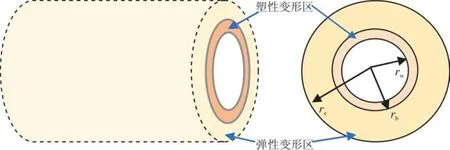
图1 热采水平井塑性破坏半径求解模型示意Fig.1 Diagram of formation plastic damage radius solving model

1.1 原地主应力对近井地应力的影响

水平井原地主应力方向与井筒轴向不一致，计算过程中需要将地应力分量的表达式进行坐标变换，变换到与井轴一致的柱坐标系上[7-8](见图2).文献[2]应用叠加原理得到柱坐标系下水平井近井地带弹性区应力分布计算模型，并且证明水平井近井地层承受的切应力很小，在计算中可以忽略.因此，原地应力造成的水平井近井应力分布规律可以表示为

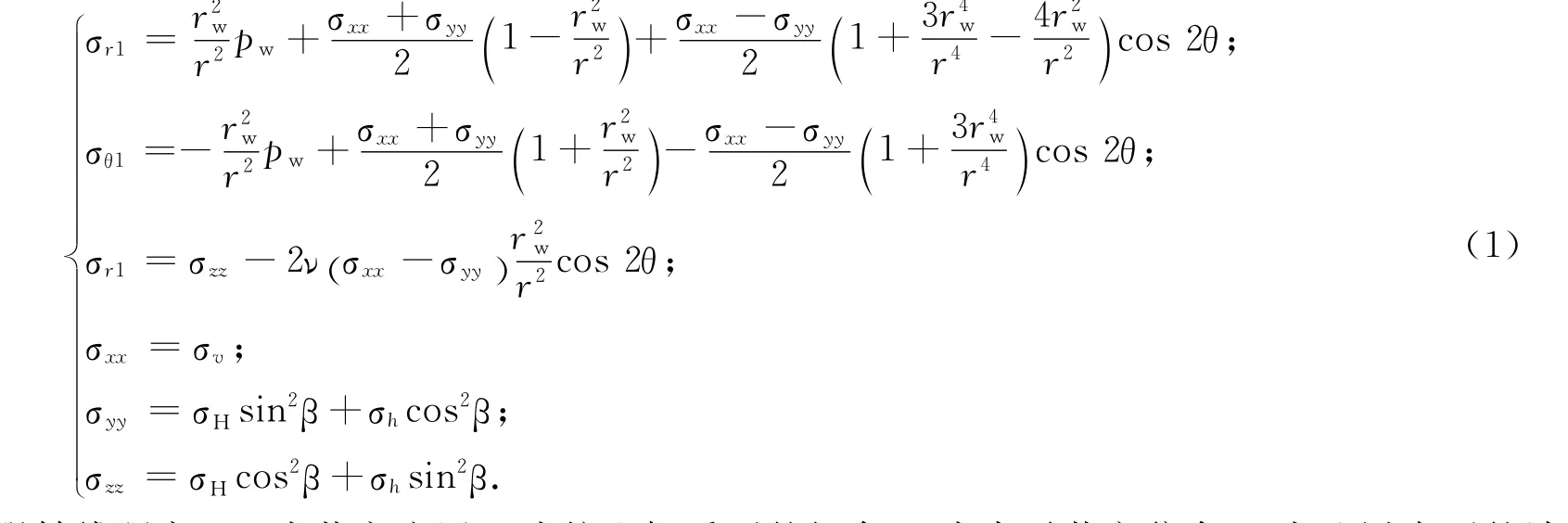
式中：r为距井眼轴线距离；pw为井底流压；θ为柱坐标系下的极角；β为水平井方位角；ν为地层岩石的泊松比，无量纲；σH、σh、σv分别为原始地层最大水平主应力、最小水平主应力、垂向主应力；σr1、σθ1、σz1分别为原地应力产生的柱坐标系下近井弹性区径向、周向和轴向应力.

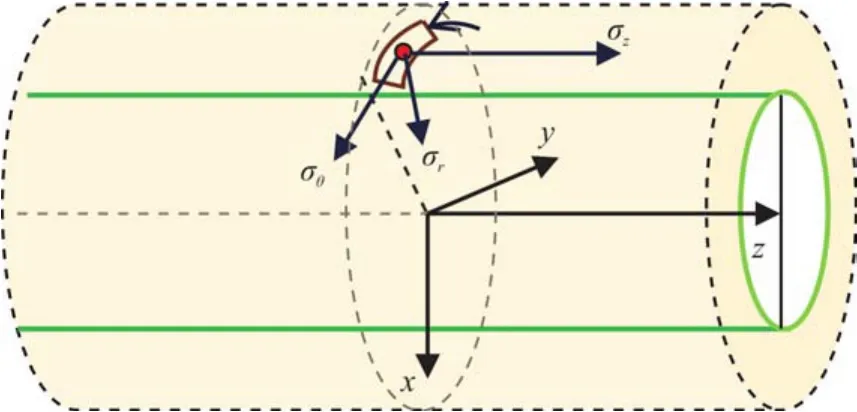
图2 水平井井筒周围应力分析模型坐标转换示意Fig.2 Coordinate transformation diagram of stress analysis around horizontal wellbore

1.2 井壁渗透性对近井地层附加应力的影响

稠油热采水平井开发过程中，井底高压注入使流体向地层孔隙中径向流动，造成近井地应力的变化[11-12].由地层渗透性造成的近井弹性区附加应力表达式为

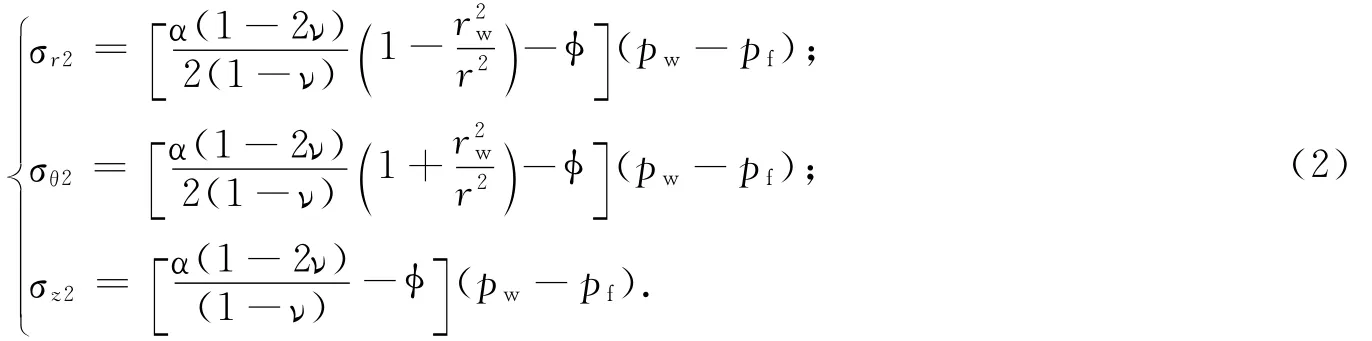
式中：σr2、σθ2、σz2分别为高压注入条件下井壁渗透性产生的近井径向、周向和轴向附加应力；α为岩石Biot弹性因数，无量纲；φ为岩石的孔隙度，无量纲；pf为原始地层压力.

1.3 注汽温度效应对热应力分布的影响

稠油热采水平井开发过程中，近井地带储层受注入蒸汽(或其他热源)的加热影响而承受温度载荷，由于近井地层岩石在某些方向的热胀冷缩受到限制，从而产生热应力[12].假设地层温度变化为一维稳态导热，则近井弹性区热应力的表达式为

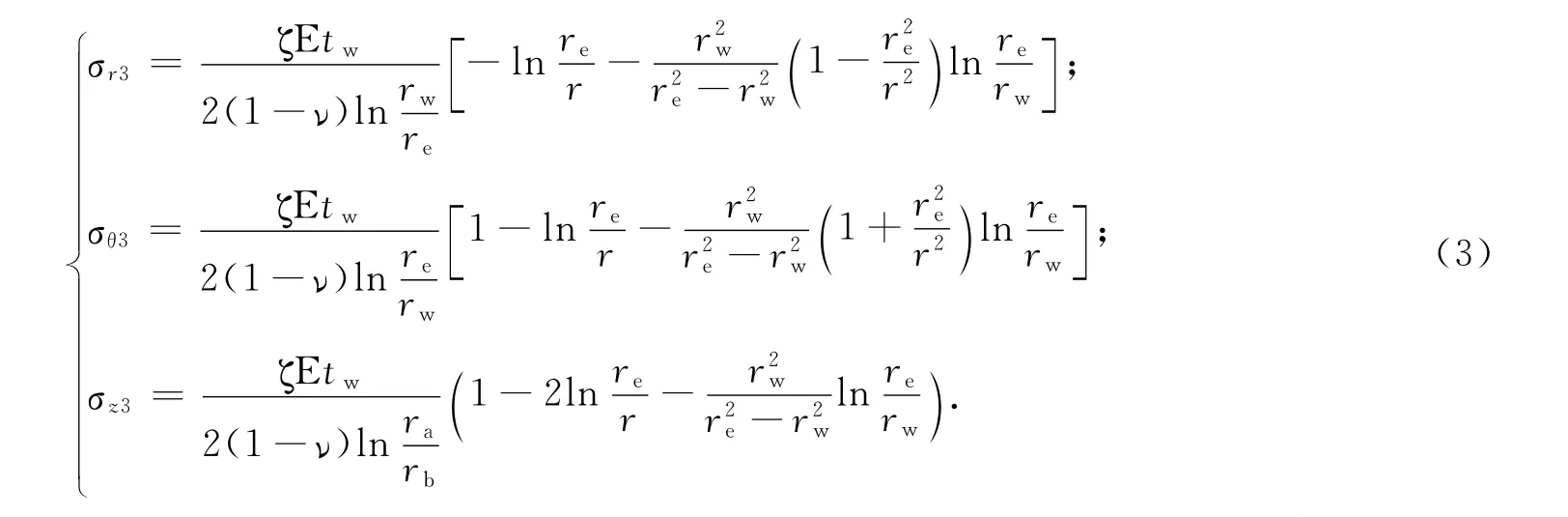
式中：σr3、σθ3、σz3分别为井底注汽温度效应产生的近井径向、周向和轴向附加应力；tw为热采条件下井底温度变化量，tw=Tw-Tf，Tw、Tf分别为当前井底温度和原始地层温度；ζ为岩石的线热胀系数；E为储层岩石的弹性模量.

1.4 近井地层应力计算模型

热采水平井近井地应力受到原始地层应力、井身结构、地层渗透性、井底流压等因素的影响，将各种因素造成的地应力相互迭加，得到热采水平井近井弹性区地应力分布的计算模型为

判断近井地层塑性破坏半径需要将近井地应力分布模型代入岩石破坏强度准则求解.由于强度判别准则多采用主应力表示，因此需要将柱坐标系下的应力计算模型转化成主应力形式的.在生产过程中，井眼附近的应力分布是不断变化的，主应力也随之变化，柱坐标系下近井地层应力的主应力形式[5]为

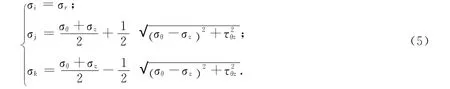
式中：i、j、k可取1，2，3.在忽略切向应力的影响条件下，近井地层岩石最大主应力、中间主应力和最小主应力[6，13]分别为

2 塑性破坏半径求解方法

2.1 近井岩石塑性破坏基本判据

当井眼周围岩石应力和应变达到一定极限时，岩体由弹性状态进入非弹性状态.如果应力、应变继续增加，井壁出现宏观裂纹，并且塑性破坏区半径不断增大.近井岩石的塑性破坏状态用岩石破坏准则描述，选取Mohr-Coulomn准则、Drucker-Prager准则、Hoek-Brown准则作为热采水平井塑性破坏的判据.

考虑地层孔隙流体压力的Mohr-Coulomn准则判别式为

考虑中间主应力对岩石塑性破坏的Drucker-Prager准则判别式为

式中：J1、J2分别为第一、第二偏应力不变量；C0、C1分别为中间系数，可以根据岩石抗压强度和内摩擦角求得.

基于抛物线型岩石破坏包络线的Hoek-Brown准则判别式为

式中：σc为岩石单轴抗压强度；m、s为经验因数.

2.2 近井塑性破坏半径预测方法

近井地层的塑性破坏从井壁开始并向外延伸[13-14]，随着距井轴半径的增大，地层有效应力不断下降.在地层外边界处，地层主应力等于原地主应力.当某一点的主应力条件不满足岩石破坏准则时，塑性破坏终止，该点范围外的地层不发生塑性破坏.因此，需要提出不同破坏准则条件下的近井岩石屈服函数.

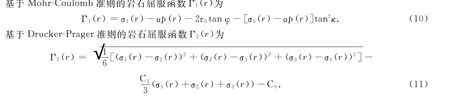
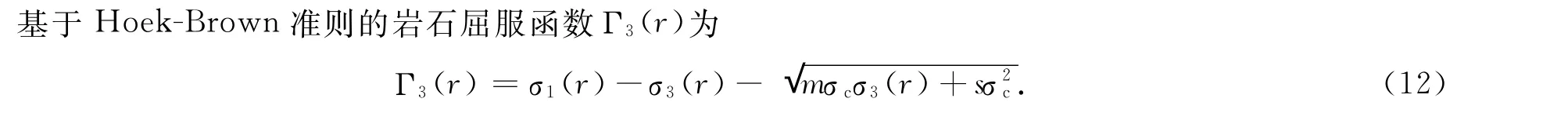
由于热采水平井近井地层应力是距井轴半径的函数，在一定生产条件下屈服函数的零点对应的半径即为热采水平井近井地层的塑性破坏半径.当塑性屈服函数值大于0时，岩石发生塑性破坏，且函数值越大，岩石的塑性破坏程度越高，出砂越严重；当塑性屈服函数值小于0时，岩石处于弹性变形状态.该方法不考虑近井塑性破坏区的塑性应力分布状态，省去求解近井塑性破坏区塑性应力的复杂推导过程，操作方便.

3 算例及塑性破坏半径敏感性分析

3.1 基础数据

渤海油田某疏松砂岩稠油油藏采用热采水平井开发，出砂严重.为了分析该井井底出砂状况，准确评价出砂程度和采取针对性的防砂施工，需要预测热采条件下的近井塑性破坏半径.编写计算机程序，模拟热采水平井近井塑性破坏半径的变化规律.模拟计算井基本参数见表1.计算模型因数及井底注热因数见表2.

表1 渤海油田模拟计算井基本参数Table 1 Basic data of the cited well in Bohai oilfield

表2 渤海油田水平井注热参数及模型计算因数Table 2 Injecting parameters of the cited well in Bohai oilfield and model coefficients

3.2 算例计算结果

热采水平井近井地层应力随半径的变化规律见图3.由图3可知，随着半径的变化，求解单元体上的主应力与柱坐标系下应力的关系不是固定不变的，随着半径的增大，径向应力先增大后减小，轴向应力和周向应力不断减小.

将近井地层应力转化为主应力的形式代入塑性屈服函数表达式(10～12)，可得塑性屈服函数随半径的变化规律，塑性屈服函数值的零点对应的半径即为热采水平井的塑性破坏半径(见表3).在0～360°内变化井周角，求解不同井周角条件下的地层破坏半径，可得塑性半径沿井周的分布规律(见图4，其中RM-C、RH-B、RD-P分别为基于Mohr-Coulomb准则、Hoek-Brown准则和Drucker-Prager准则的地层塑性破坏半径).由图4可知，井周塑性破坏半径随着井周角的变化而变化，并且井筒水平方向上的塑性破坏半径最大，垂直方向的塑性破坏半径最小.

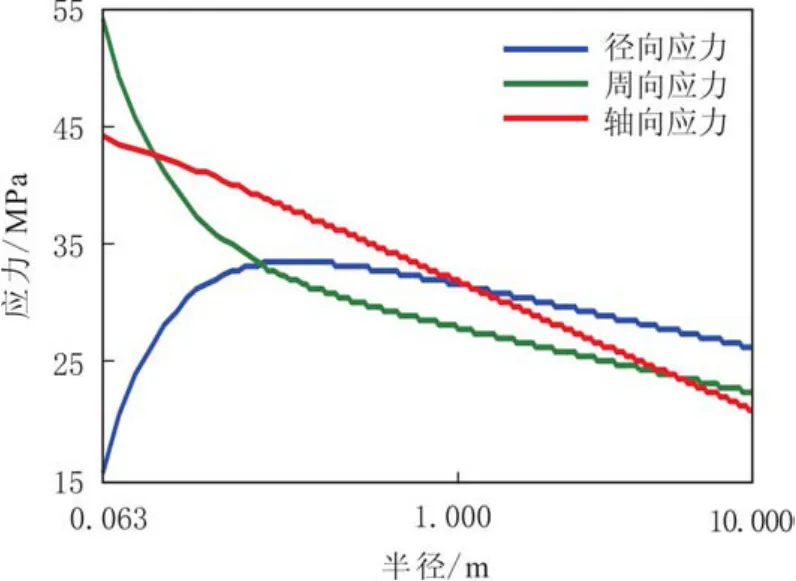
图3 热采水平井近井地层应力随半径的变化规律Fig.3 Stress varying pattern along with radius of thermal recovery horizontal wells

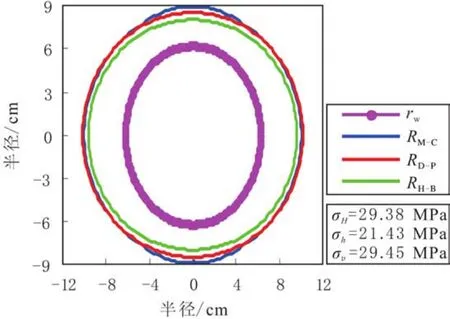
图4 基于不同塑性屈服函数的塑性破坏半径沿井周的变化规律(σH＞σv＞σh)Fig.4 Plastic damage radius around wellbore based on different failure functions(σH＞σv＞σh)

表3 渤海油田基于不同岩石破坏准则的地层塑性破坏半径预测结果Table 3 Plastic damage radius of the cited well in BoHai oilfield based on different rock failure criterions

3.3 原地主应力顺序对塑性破坏半径的影响

为了验证原地主应力顺序对近井塑性破坏半径的影响，假设除原地主应力以外的模拟参数分别与表1、表2相同，分别研究σH＞σv＞σh、σv＞σH＞σh、σH＞σh＞σv条件下塑性破坏半径的分布规律(见图5).由图5可知，当σv＞σH时，井周垂直方向上的塑性破坏半径最大(见图5(a))；当σH＞σv时，井周水平方向上的塑性破坏半径最大(见图5(b)).

在一定的注热生产条件下，采用不同的岩石破坏准则建立屈服函数，预测得到的塑性破坏半径不同，采用Drucker-Prager准则和Hoek-Brown准则建立屈服函数预测结果偏小的原因是没有考虑井底流压的影响.

3.4 温度对塑性破坏半径的影响

不同温度下基于Mohr-Coulomb准则的屈服函数变化规律，以及井周塑性破坏半径随温度的变化规律分别见图6和图7.由图6和图7可知，随着井底温度的升高，塑性屈服函数值零点右移，塑性破坏半径增大；内边界处(井壁)塑性屈服函数值随井底温度的升高而不断增大，可以判断随着井底温度的升高，井壁的塑性破坏程度加剧.

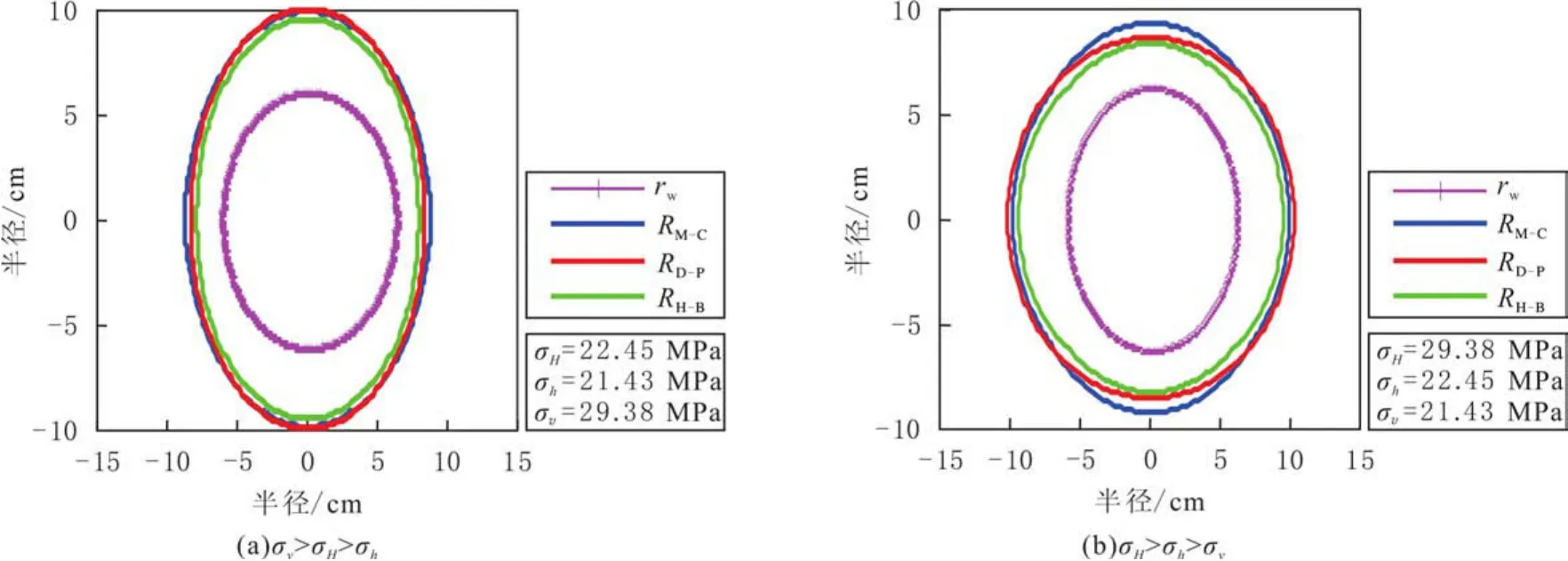
图5 不同原地主应力条件下塑性破坏半径沿井周的分布曲线Fig.5 Plastic damage radius around wellbore under different original stress orders

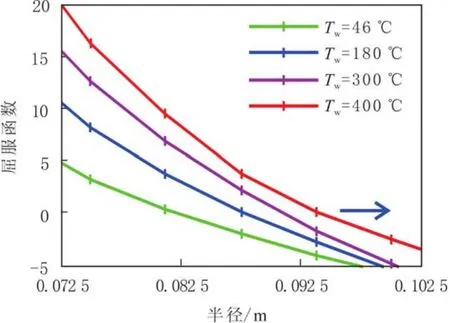
图6 温度对屈服函数及塑性破坏半径的影响Fig.6 Temperature influence on failure functions and plastic damage radius

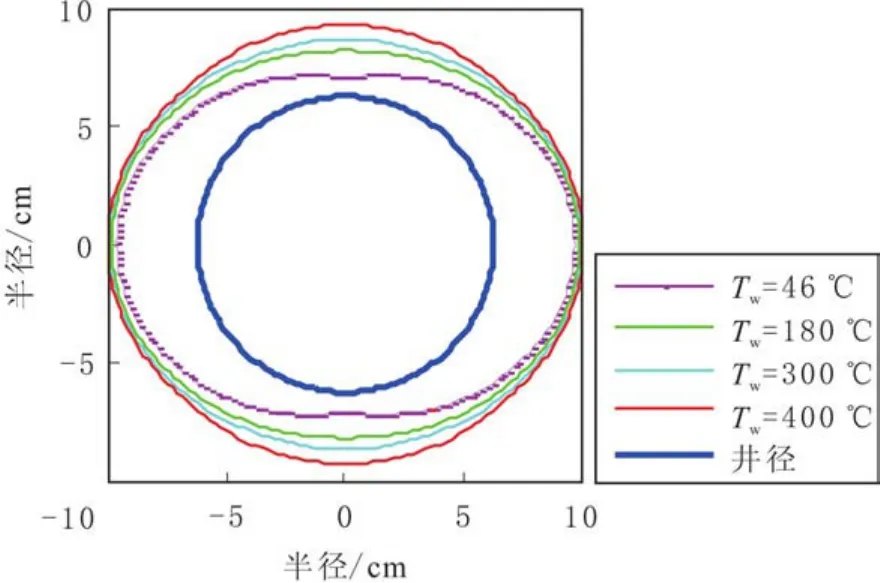
图7 不同温度下塑性破坏半径沿井周的分布规律Fig.7 Plastic damage radius varying pattern around wellbore under different temperatures

3.5 井底流压对塑性破坏半径的影响

不同井底流压下基于Mohr-Coulomb准则的塑性屈服函数变化规律，以及塑性破坏半径的分布规律见图8和图9.由图8和图9可知，井底流压对塑性破坏半径的影响较小；但随着井底流压的增大，井壁屈服函数值不断减小，可以推断高压注汽条件下井底高压促使井壁稳定性增强.

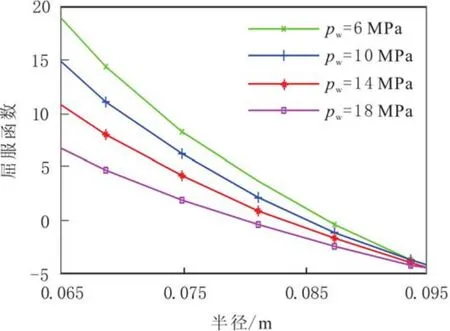
图8 井底流压对屈服函数及塑性破坏半径的影响Fig.8 Inflow pressure influence on failure functions and plastic damage radius

图9 不同井底流压下塑性破坏半径沿井周的分布规律Fig.9 Plastic damage radius varying pattern around wellbore under different inflow pressure

3.6 水平井井眼方位角塑性破坏半径的影响

在128.26°井周角下，模拟基于Mohr-Coulomb准则的塑性屈服函数及近井塑性破坏半径随水平井眼方位角的变化规律(见图10和图11).由图10和图11可知，当水平井井眼平行于最大水平主应力方向(β =0°或180°)时，井周塑性破坏半径最大；当水平井眼垂直于最大水平主应力方向(β=90°或270°)时，井周塑性破坏半径最小.随着水平井井眼与最大水平主应力方向夹角的增大，井周塑性破坏半径受方位角的影响程度减小.

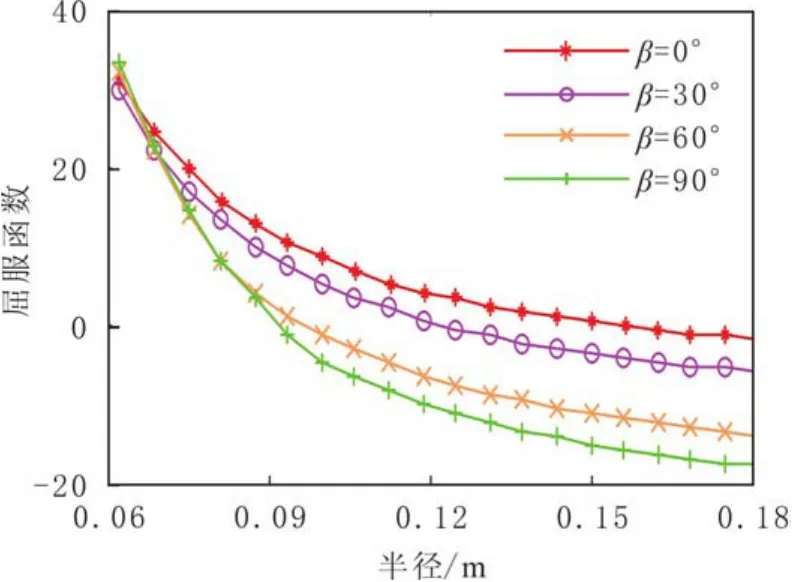
图10 屈服函数及塑性破坏半径随水平井方位角的影响Fig.10 Azimuthal angle influence on failure functions and plastic damage radius

4 结论

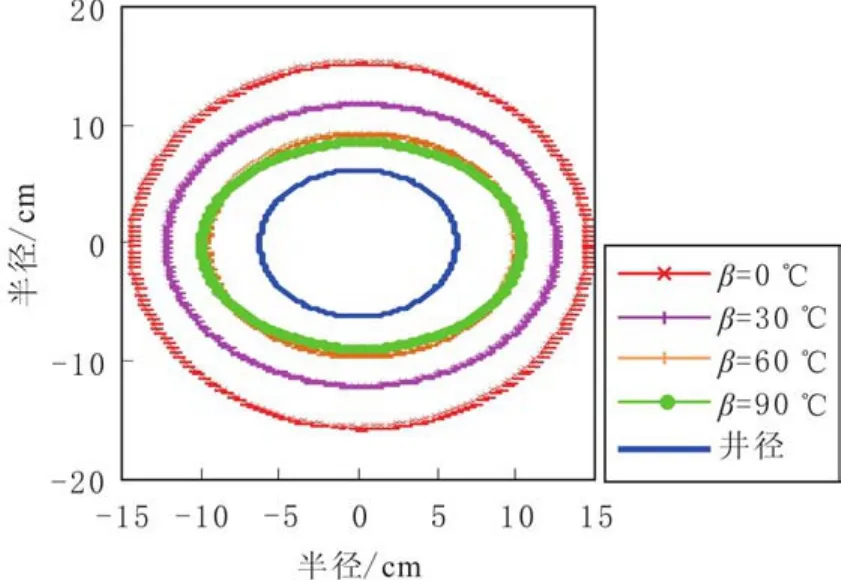
图11 不同井眼方位角下塑性破坏半径沿井周的分布规律Fig.11 Plastic damage radius varying pattern around wellbore under different azimuthal angle

(1)建立热采复杂条件下的近井塑性破坏半径预测方法，应用岩石塑性屈服函数求解塑性破坏半径，具有普适性，操作简单.

(2)井壁处塑性屈服函数值越大，井壁破坏程度越大，出砂越严重；温度越高，塑性破坏半径越大，井底出砂区域越大.塑性破坏半径受井底温度、原地主应力顺序、井周角、方位角、井底流压等因素的影响.

(3)当垂向主应力大于水平主应力时，垂直方向上的塑性破坏半径最大；反之，井周水平方向上的塑性破坏半径最大.当水平井方位角为0°(或180°)时，井周塑性破坏半径最大；当水平井方位角为90°(或270°)时，井周塑性破坏半径最小.

[1] Nunes M，Bedrikovetsky P，Paiva R，et al.Theoretical definition of formation damage zone with applications to well stimulation[J]. Journal of Energy Resources Technology，2010，132(3)：468-474.

[2] 董长银，王爱萍.出砂水平井近井塑性区出砂半径预测研究[J].中国矿业大学学报，2012，41(4)：663-668.

Dong Changyin，Wang Aiping.Distribution of plastic stress near wellbore and prediction of sanding radius for sanding horizontal well [J].Journal of China University of Mining&Technology，2012，41(4)：663-668.

[3] 曾聪，马保松，刘厚平.水平定向钻穿越施工中钻井液渗透对孔壁塑性半径的影响[J].中国石油大学学报：自然科学版，2013，37(2)：57-61.

Zeng Cong，Ma Baosong，Liu Houping.Effect of drilling fluid penetration on plastic radius of horizontal directional drilling borehole [J].Journal of China University of Petroleum：Natural Sciences Edition，2013，37(2)：57-61.

[4] Nunes M JS，Bedrikovetsky P G，Newbery B，et al.Formation damage zone radius and its applications to well stimulation[C]//The 8th European Formation Damage Conference.Scheveningen：122843-MS，2009.

[5] 郭春华.井眼应力分布模拟及井壁稳定性研究[D].成都：成都理工大学，2011.

Guo Chunhua，Simulation of in-situ stress near wellbore and research on wellbore stability[D].Chengdu：Chengdu University of Technology，2011.

[6] Smart E G D，Somerville J M，MacGregor K J.The prediction of yield zone development around a borehole and its effect on drilling and production[C]//The 32nd US Symposium on Rock Mechanics(USRMS).Norman：91-961-ARMA，1991.

[7] Hsiao C.Growth of plastic zone in porous medium around a wellbore[C]//Offshore Technology Conference.Houston：5858-MSOTC，1988.

[8] Lee Y K，Pietruszczak S.A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rock mass[J].Tunneling and Underground Space Technology，2008，23(5)：588-599.

[9] Younessi A，Rasouli V，Wu B.Numerical Simulations of Sanding Under Different Stress Regimes[C]//The 46th US Rock Mechanics Geomechanics Symposium.Chicago：ARMA-12-373，2012.

[10] Nawrocki P A，Dusseault M B.Modelling of damaged zones around openings using radius-dependent Young's modulus[J].Rock Mechanics and Rock Engineering，1995，28(4)：227-239.

[11] 王爱萍.水平井地应力及出砂预测研究[D].青岛：中国石油大学，2011.

Wang Aiping.Research on the stress distribution and sanding prediction model for horizontal well[D].Qingdao：China University of Petroleum，2011.

[12] 王文星.岩石力学公式速查手册[M].长沙：中南大学出版社，2012：107-112.

Wang Wenxing.Fast lookup handbook of rock and soil mechanics formulas[M].Changsha：CSU Press，2012：107-112.

[13] 李玉伟，李修辅，刘佳，等.深井重复压裂裂缝起裂模型[J].大庆石油学院学报，2009，30(5)：64-67.

Li Yuwei，Li Xiufu，Liu Jia，et al.Fracture Initiation model during re-fracturing in deep wells[J].Journal of Daqing Petroleum Institute，2009，30(5)：64-67.

[14] 尹洪军，杨春城，徐子怡，等.分段压裂水平井压力动态分析[J].东北石油大学学报，2014，38(3)：75-81.

Yin Hongjun，Yang Chuncheng，Xu Ziyi，et al.Dynamic pressure analysis in staged fracturing horizontal wells[J].Journal of Northeast Petroleum University，2014，38(3)：75-81.

TE257

A

2095-4107(2014)05-0103-08

DOI 10.3969/j.issn.2095-4107.2014.05.013

2014-06-03；编辑任志平

国家自然科学基金项目(51374226)

李彦龙(1989-)，男，硕士研究生，主要从事油气井防砂完井、固液多相流方面的研究.